二叉树的结构定义:
public class BinaryTree {
//内部类 表示一个结点
static class TreeNode {
TreeNode left; //左子树
TreeNode right; //右子树
char value; //结点值
TreeNode(char value) {
this.value = value;
}
}
public TreeNode root; //根节点
...
}二叉树的基本操作包括:
// 前序遍历
void preOrder(Node root);
// 中序遍历
void inOrder(Node root);
// 后序遍历
void postOrder(Node root);
// 获取树中节点的个数
int size(Node root);
// 获取叶子节点的个数
int getLeafNodeCount(Node root);
// 获取第K层节点的个数
int getKLevelNodeCount(Node root,int k);
// 获取二叉树的高度
int getHeight(Node root);
// 检测值为value的元素是否存在
Node find(Node root, int val);
//层序遍历
void levelOrder(Node root);
// 判断一棵树是不是完全二叉树
boolean isCompleteTree(Node root);本文以二叉树的几种基本操作为例,介绍实现二叉树操作的两种常见思路:遍历思路与子问题思路。
目录
一、二叉树的遍历思路与子问题思路
1、遍历思路
2、子问题思路
3、图示
二、二叉树的基本操作
1、获取树中结点的个数
遍历思路
子问题思路
复杂度分析
2、获取叶子节点的个数
遍历思路
子问题思路
3、获取第K层结点的个数
子问题思路
4、求树的高度
子问题思路
复杂度分析
5、二叉树的中序遍历
遍历思路
子问题思路
6、二叉树的后序遍历
遍历思路
子问题思路
7、检测值为value的元素是否存在,若存在返回该元素的结点
子问题思路
一、二叉树的遍历思路与子问题思路
在二叉树是递归定义的,在二叉树相关的习题中也常常需要运用到递归。遍历思路与子问题思路是递归解决二叉树问题的两种常见思路。下面以“前序遍历二叉树”为例,简要介绍这两种思路及其实现。
题干
LeetCode 144. 二叉树的前序遍历
设计一个方法,给定二叉树的根节点
root,返回它节点值的 前序 遍历。
注意:在力扣提供的代码模板中,前序遍历的方法是带有返回值List<Integer>的。因此,我们需要自行定义一个List<Integer> list集合来存放结果。
1、遍历思路
遍历思路很好理解:递归依次访问二叉树中的元素,每遇到一个元素就进行一次操作。例如:每遇到一个元素,就将这个元素打印;或每遇到一个元素,就使计数器加一。
在这道前序遍历的题中,遍历思路体现在:每递归到一个元素,就将这个元素放入list集合中。
依照这个思路,我们可以写出以下代码:
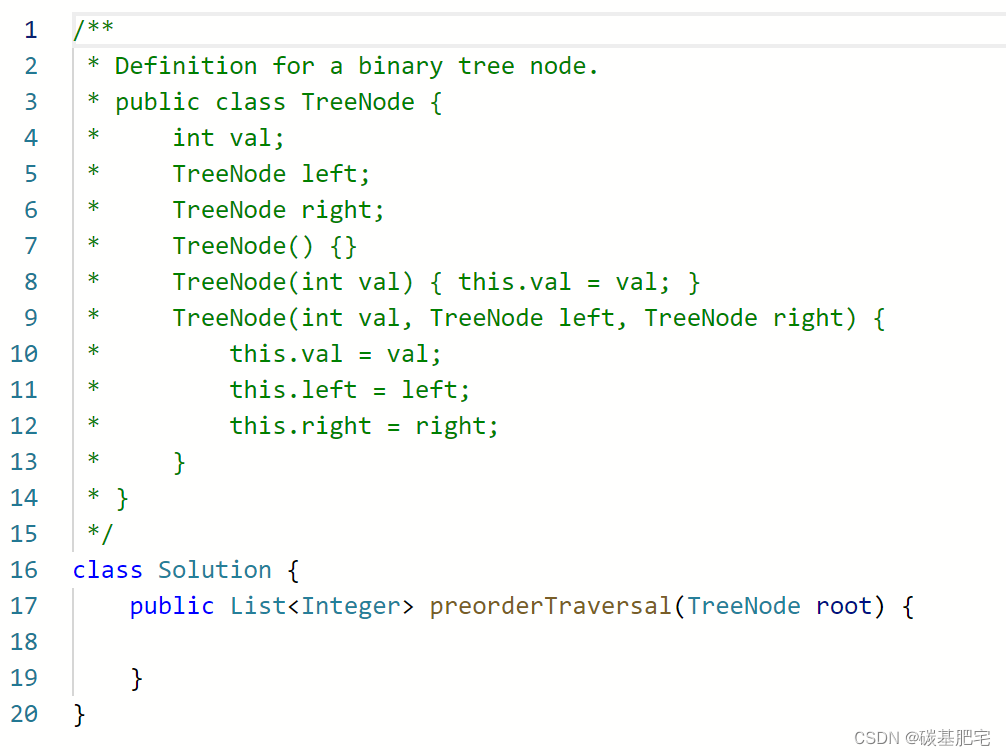
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> list = new ArrayList<>(); //创建存储结果的集合list
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null) {
return list;
}
list.add(root.val); //将当前元素加入集合list
preorderTraversal(root.left); //递归左树
preorderTraversal(root.right); //递归右数
return list; //返回结果
}
}但是,事实上这样的解答并不是很好,因为代码模板中给定的前序遍历方法是有返回值的。而上面的代码在递归时并没有接收返回值。也就是说,它的返回值被忽略的。
事实上,如果采用上面这种思路编写该代码,不需要返回值也是可行的:
public class BinaryTree {
List<Integer> list = new ArrayList<>(); //创建存储结果的集合list
//前序遍历
public void preorderTraversal(TreeNode root) {
if(root == null) {
return;
}
list.add(root.val); //将当前元素加入集合list
preorderTraversal(root.left); //递归左树
preorderTraversal(root.right); //递归右数
}
}或是拆成两个方法书写,本质不变但有细微改动:
public List<Integer> preorderTraversal_(TreeNode root) {
List<Integer> list = new ArrayList<>();
preOrder(root,list);
return list;
}
public void preOrder(TreeNode root,List<Integer> list) {
if(root == null) {
return;
}
list.add(root.value);
preOrder(root.left,list);
preOrder(root.right,list);
}
或是抛开该题,不用集合存放,直接以打印的方式输出前序遍历结果:
public class BinaryTree {
//前序遍历
public void preorderTraversal(TreeNode root) {
if(root == null) {
return;
}
System.out.print(root.value + " ");
preOrder(root.left);
preOrder(root.right);
}
}如此,每遇到一个元素,就将其放入list集合中。而list集合是成员变量,可以直接通过该类的对象进行访问。注意,由于所有元素都将存放在同一个list集合,这个list集合要定义成成员变量,放在方法的外面。如果放在了方法的内部,那么每一次递归,都将创建一个新的list,最终返回的list便不再是存放了所有元素的集合了。
2、子问题思路
子问题思路是将一个整体的大问题不断分割成规模更小但逻辑相同的小问题,再将小问题得到的结果整合到一块中。例如,校长要统计一个学校的所有学生人数,但校长不亲自直接清点每个学生,不一个一个地数,而是派任务给院长,让院长来统计每个院的人数;院长再让班长统计每个班的人数。如此,班长汇总后的结果上报给院长,院长汇总后的结果再上报给校长,校长便知道了整个学校的人数。
这样的表述可能有些抽象,我们代入到前序遍历的解题中,应该会更好理解。
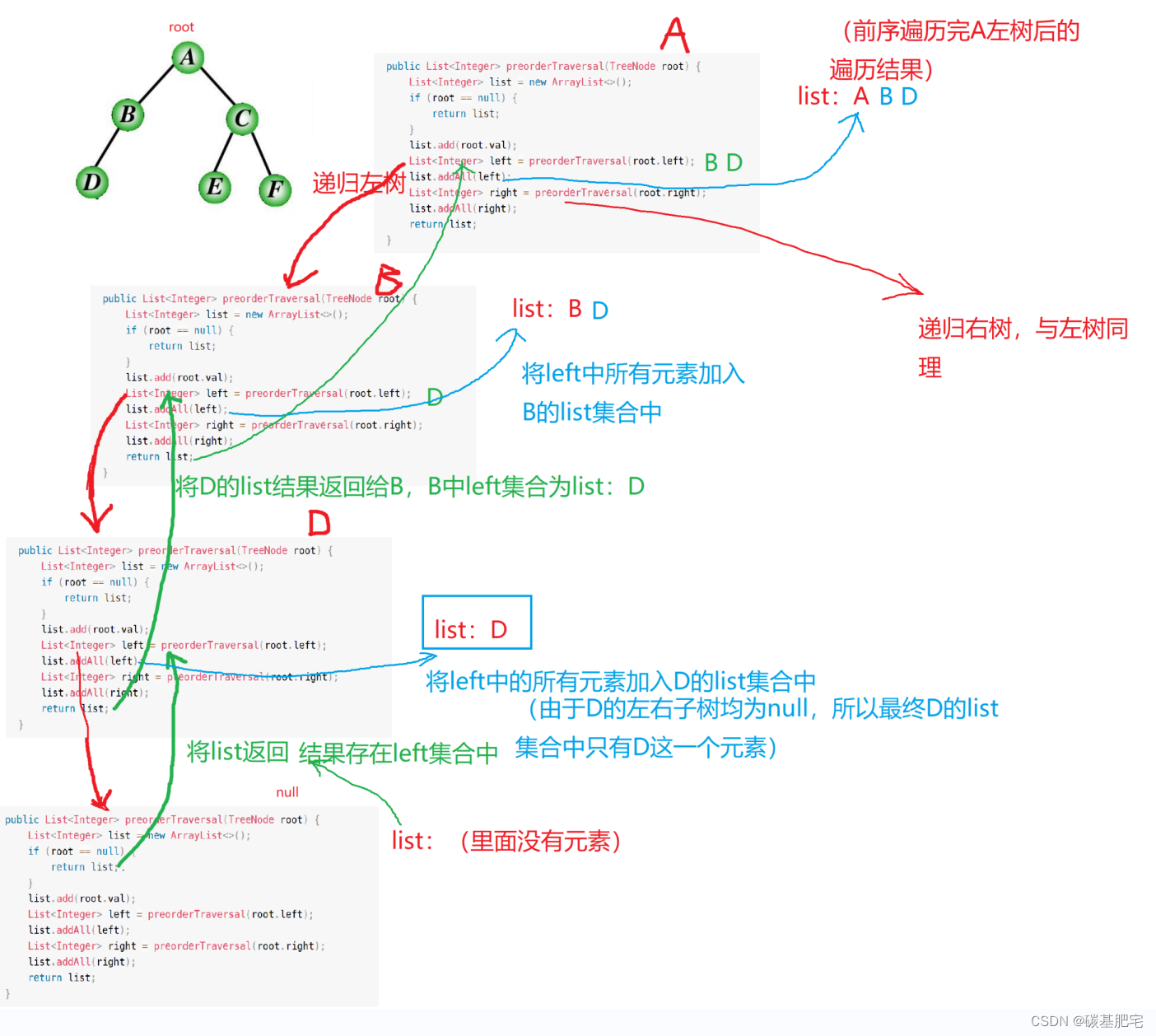
在本题中采取子问题思路:前序遍历整棵二叉树 = 前序遍历左子树+前序遍历右子树。
我们可以充分用上方法的返回值。在这个方法内部,创建集合List<Integer> list,每执行这个方法,都创建一个集合list,代表遍历到当前元素时的遍历结果。将当前元素存入list集合中。
再定义List<Integer> left与List<Integer> right集合,分别接收递归左子树与递归右子树的返回值,即记录左子树与右子树的遍历结果。
获取到左子树的遍历结果后,通过list.addAll()立即将左子树的结果加入list集合;获取到右子树的遍历结果后,也同样立即将右子树的遍历结果加入到list集合。如此往复,到该二叉树的根结点时,就能获取到整棵树的遍历结果,最终将list返回即可。
因此,代码如下:
public List<Integer> preorderTraversal(TreeNode root) {
//在方法内部创建集合 存放结果
List<Integer> list = new ArrayList<>();
if (root == null) {
return list;
}
list.add(root.val); //将当前元素加入集合中
List<Integer> left = preorderTraversal(root.left); //递归遍历左树
list.addAll(left); //将左树遍历结果加入当前集合中
List<Integer> right = preorderTraversal(root.right); //递归遍历右树
list.addAll(right); //将右树遍历结果加入当前集合中
return list;
}3、图示
如下是前序遍历A的左子树的示意图。
二、二叉树的基本操作
1、获取树中结点的个数
遍历思路
定义成员变量size作计数器,每遇到一个结点,令size++,最终统计出所有结点个数。注意,该写法有一定的缺陷。当对同一个对象调用两次size()方法时,size的数值会叠加。即使加static,也会有不同对象调用size()方法时的数值叠加问题,从而导致结果错误。
//获取二叉树中节点个数 遍历思路
public int size;
public void size(TreeNode root) {
if(root == null) {
return;
}
this.size++;
size(root.left);
size(root.right);
}子问题思路
整个二叉树结点个数 = 左子树的节点个数+右子树的节点个数+1(自己本身)。保存递归后的左子树结点个数与右子树结点个数,left+right+1即所求。
//获取二叉树中节点个数 子问题思路
public int size(TreeNode root) {
if(root == null) {
return 0;
}
int left = size(root.left);
int right = size(root.right);
return left+right+1;
}复杂度分析
时间复杂度:O(N) (要递归二叉树上的每一个结点)
空间复杂度:O(logN) (递归一定会在栈上开辟内存。而在递归右子树时,左子树已经递归完了。即给右子树开辟栈帧时,左子树的栈帧不会同时占用。在满二叉树的情况下,递归开辟的内存空间就等于二叉树的高度。当然,如果是单分支的树,那么空间复杂度就是O(N)。但一般这样的情况较少。)
2、获取叶子节点的个数
遍历思路
用成员变量leafCount标记叶子节点的数目。当左子树与右子树都为null时,这个结点是叶子结点,此时令leafCount++即可。
//获取叶子节点的个数
int leafCount;
public void getLeafNodeCount3(TreeNode root) {
if(root == null) {
return;
}
if(root.left == null && root.right == null) {
leafCount++;
}
getLeafNodeCount(root.left);
getLeafNodeCount(root.right);
}子问题思路
整棵二叉树的叶子结点个数 = 左子树的叶子结点个数+右子树的叶子结点个数
叶子结点 = 左子树和右子树都为null的结点
掌握这两个结论,可以写出如下代码:
//获取叶子节点的个数
public int getLeafNodeCount2(TreeNode root) {
if(root == null) {
return 0;
}
if(root.left == null && root.right == null) {
return 1;
}
int left = getLeafNodeCount2(root.left); //左子树中叶子节点的个数
int right = getLeafNodeCount2(root.right); //右子树中叶子节点的个数
return left+right;
}或
//获取叶子节点的个数
public int getLeafNodeCount(TreeNode root) {
if(root == null) {
return 0;
}
int left = getLeafNodeCount(root.left);
int right = getLeafNodeCount(root.right);
if(left == 0 && right == 0) {
return 1;
}
return left+right;
}从结果上看。两段代码都是正确的。
注意:在一些问题上,子问题的思路分析能够使问题变得更清晰、简便。
3、获取第K层结点的个数
子问题思路
该题的思路比较巧妙。要求第K层的结点个数,一整棵树的第K层 = 它的左子树的第K-1层 = 它的右子树的第K-1层。
一棵树第K层的结点个数 = 左子树第K-1层的结点个数+右子树第K-1层的结点个数。

可以写出如下代码,如果对代码不理解,可以参照前序遍历的图示将递归画图展开。
//获取第k层结点的个数
public int getKLevelNodeCount(TreeNode root,int k) {
if(root == null) {
return 0;
}
if(k == 1) {
return 1;
}
int left = getKLevelNodeCount(root.left,k-1);
int right = getKLevelNodeCount(root.right,k-1);
return left+right;
}4、求树的高度
🔗LeetCode-104. 二叉树的最大深度
子问题思路
根据二叉树高度的定义:树的高度或深度是树中结点的最大层次。
一棵二叉树的高度 = 左子树高度与右子树高度的最大值 + 1
由此通项公式,可以写出求二叉树高度的代码:
//二叉树的高度
public int getHeight(TreeNode root) {
if(root == null) { //空树高度为0 返回0
return 0;
}
int left = getHeight(root.left); //记录左子树的高度
int right = getHeight(root.right); //记录右子树的高度
return Math.max(left,right) + 1; //返回左子树和右子树的高度的最大值+1,即树的高度
}特别注意:若不用变量left和right保存左右子树的高度递归结果,而是直接将递归语句代入求最大值的语句,是不合适的:

虽然在本地IDE中运行,结果不会有错,但在在线OJ中运行,会超出时间限制。因为没有用额外的变量来保存递归结果的话,最终return语句中实际上有四个递归语句,有大量的递归的重复计算,这是非常耗时的。
复杂度分析
时间复杂度:O(N),每一个结点都要求一次以它为根的树的高度,也就是每一个结点实际都会访问的。
空间复杂度:O(height),和树的高度有关系。若是单分支的树,则高度为N,空间复杂度即为O(N),若是满二叉树,则高度为logN,空间复杂度即为O(logN。
5、二叉树的中序遍历
与前面前序遍历的代码相似,只是改变了对元素的操作与递归左右子树的顺序(左根右)。
遍历思路
//中序遍历 递归 遍历思路
public void inOrder(TreeNode root) {
if(root == null) {
return;
}
inOrder(root.left);
System.out.print(root.value + " ");
inOrder(root.right);
}子问题思路
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) {
return list;
}
List<Integer> left = inorderTraversal(root.left);
list.addAll(left);
list.add(root.val);
List<Integer> right = inorderTraversal(root.right);
list.addAll(right);
return list;
}
}6、二叉树的后序遍历
与前面前序遍历的代码相似,只是改变了对元素的操作与递归左右子树的顺序(左右根)。
遍历思路
//后序遍历 递归 遍历思路
public void postOrder(TreeNode root) {
if(root == null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.value + " ");
}子问题思路
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) {
return list;
}
List<Integer> left = postorderTraversal(root.left);
list.addAll(left);
List<Integer> right = postorderTraversal(root.right);
list.addAll(right);
list.add(root.val);
return list;
}
}7、检测值为value的元素是否存在,若存在返回该元素的结点
子问题思路
检测值为value的元素在整棵二叉树是否存在 = 检测左树是否存在该节点(如果存在便结束检测并返回) + 检测右树是否存在该结点(如果存在便结束检测并返回)
该代码的思路类似于前序遍历的思路。每遍历到一个结点,就判断这个结点的值是否与给定的value相匹配。
//检测值为value的元素是否存在 子问题思路
public TreeNode find(TreeNode root, int val) {
if(root == null) {
return null;
}
if(root.value == val) {
return root;
}
TreeNode left = find(root.left,val);
if(left != null) {
return left;
}
TreeNode right = find(root.right,val);
return right;
}