机器学习笔记之K近邻学习算法
- 引言
- 回顾:投票法
- 回顾:明可夫斯基距离
- K \mathcal K K近邻算法
- 算法描述
- K \mathcal K K值的选择
- 小插曲:懒惰学习与急切学习
- KD \text{KD} KD树描述及示例
- K \mathcal K K近邻 VS \text{ VS } VS 贝叶斯最优分类器
引言
本节将介绍 K \mathcal K K近邻学习算法的理论描述。
回顾:投票法
详见《机器学习》(周志华著) P182 8.4.2 投票法
在介绍集成学习—— Bagging \text{Bagging} Bagging中针对分类任务,通常以多数表决的方式决定样本最终预测的归属类别,这种方式能够有效消除样本预测结果的方差信息。
当然,投票法( Voting \text{Voting} Voting)并非只有多数表决一种方式,这里整理了几种投票方式:
- 场景构建:
已知数据集合 D = { ( x ( i ) , y ( i ) ) } i = 1 N \mathcal D = \{(x^{(i)},y^{(i)})\}_{i=1}^N D={(x(i),y(i))}i=1N,针对一个多分类任务,假设其存在 K \mathcal K K个分类,并将 y ( i ) ( i = 1 , 2 , ⋯ , N ) y^{(i)}(i=1,2,\cdots,N) y(i)(i=1,2,⋯,N)所有可能取值的标签结果组成的集合 L \mathcal L L称作标记集合:
y ( i ) ∈ L = { C 1 , C 2 , ⋯ , C K } i = 1 , 2 , ⋯ , N y^{(i)} \in \mathcal L = \{\mathcal C_1,\mathcal C_2,\cdots,\mathcal C_{\mathcal K}\} \quad i=1,2,\cdots,N y(i)∈L={C1,C2,⋯,CK}i=1,2,⋯,N
在模型学习完成后,针对某个陌生样本 x ^ \hat x x^,通过某学习器 h t ( ⋅ ) h_t(\cdot) ht(⋅)预测结果记作 h t ( x ^ ) h_t(\hat x) ht(x^)。该结果可表示成一个 K \mathcal K K维向量形式,并且向量中的每一个分量 h t k ( x ^ ) ( k = 1 , 2 , ⋯ , K ) h_t^{k}(\hat x)(k=1,2,\cdots,\mathcal K) htk(x^)(k=1,2,⋯,K)表示:学习器 h t ( x ^ ) h_t(\hat x) ht(x^)在标签结果 C k \mathcal C_k Ck上的输出信息:
h t ( x ^ ) = [ h t 1 ( x ^ ) , h t 2 ( x ^ ) , ⋯ , h t K ( x ^ ) ] K × 1 T h_t(\hat x) = \left[h_t^{1}(\hat x),h_t^{2}(\hat x),\cdots,h_t^{\mathcal K}(\hat x)\right]_{\mathcal K \times 1}^T ht(x^)=[ht1(x^),ht2(x^),⋯,htK(x^)]K×1T
这个输出信息 h t k ( x ^ ) h_t^{k}(\hat x) htk(x^)可能是一个概率值 P ( C k ∣ x ^ ) ∣ h t ( ⋅ ) \mathcal P(\mathcal C_k \mid \hat x) \mid h_t(\cdot) P(Ck∣x^)∣ht(⋅);也有可能 ∈ { 0 , 1 } \in \{0,1\} ∈{0,1}。但不可否认的是, h t ( x ^ ) h_t(\hat x) ht(x^)中所有分量之和必然等于 1 1 1:因为最终只会选择一个标记作为x ^ \hat x x^标签的预测结果。通常将概率值作为输出的投票方式称为软投票 ( Soft Voting ) (\text{Soft Voting}) (Soft Voting);反之,将{ 0 , 1 } \{0,1\} {0,1}作为输出的投票方式称为硬投票 ( Hard Voting ) (\text{Hard Voting}) (Hard Voting)。
∑ k = 1 K h t k ( x ^ ) = 1 \sum_{k=1}^{\mathcal K} h_t^{k}(\hat x) = 1 k=1∑Khtk(x^)=1
相应地,假设该模型中存在 T \mathcal T T个学习器,那么必然有:
∑ t = 1 T ∑ k = 1 K h t k ( x ^ ) = T \sum_{t=1}^{\mathcal T} \sum_{k=1}^{\mathcal K} h_t^{k}(\hat x) = \mathcal T t=1∑Tk=1∑Khtk(x^)=T
- 多数表决
/
/
/绝对多数投票法
(
Majority Voting
)
(\text{\text{Majority Voting}})
(Majority Voting)。该投票法的思想是:若某标签结果得票超过半数,则预测为该结果;否则拒绝预测。
这里H ( x ) \mathcal H(x) H(x)表示包含T \mathcal T T的完整模型。可以看出H ( x ^ ) \mathcal H(\hat x) H(x^)有可能无解(拒绝预测)。若学习任务要求必须提供预测结果,该方法则退化为相对多数投票法。
H ( x ^ ) = { C k if ∑ t = 1 T h t k ( x ^ ) > 1 2 ∑ t = 1 T ∑ k = 1 K h t k ( x ^ ) Reject Otherwise \mathcal H(\hat x) = \begin{cases} \begin{aligned} \mathcal C_k \quad \text{if }\text{ }\sum_{t=1}^{\mathcal T} h_t^{k}(\hat x) > \frac{1}{2} \sum_{t=1}^{\mathcal T}\sum_{k=1}^{\mathcal K} h_t^{k}(\hat x) \end{aligned} \\ \text{Reject} \quad \text{Otherwise} \end{cases} H(x^)=⎩ ⎨ ⎧Ckif t=1∑Thtk(x^)>21t=1∑Tk=1∑Khtk(x^)RejectOtherwise - 相对多数投票法
(
Plurality Voting
)
(\text{Plurality Voting})
(Plurality Voting)。相比于绝对多数投票法,该方法就是将预测结果设置为投票最多的标签结果。若同时存在多个标签结果获得最高票数,从这些结果中随机选取一个即可:
通常将‘绝对多数投票法’,‘相对多数投票法’统称为'多数投票法'。
{ C ^ = C arg max k ∑ t = 1 T h t k ( x ^ ) H ( x ^ ) = C ^ \begin{cases} \hat {\mathcal C} = \mathcal C_{\mathop{\arg\max}\limits_{k} \sum_{t=1}^{\mathcal T} h_t^{k}(\hat x)}\\ \mathcal H(\hat x) = \hat {\mathcal C} \end{cases} ⎩ ⎨ ⎧C^=Ckargmax∑t=1Thtk(x^)H(x^)=C^ - 加权投票法。观察相对多数投票法中所有学习器
h
t
(
⋅
)
(
t
=
1
,
2
,
⋯
,
T
)
h_t(\cdot) (t=1,2,\cdots,\mathcal T)
ht(⋅)(t=1,2,⋯,T)对某标签
C
k
\mathcal C_k
Ck的权重结果均相同。加权投票法通过设置权重来区分各学习器的重要程度:
{ H ( x ^ ) = C arg max k ∑ t = 1 T W t ⋅ h t k ( x ^ ) W t ≥ 0 ; ∑ t = 1 T W t = 1 \begin{cases} \mathcal H(\hat x) = \mathcal C_{\mathop{\arg\max}\limits_{k}\sum_{t=1}^{\mathcal T} \mathcal W_t \cdot h_t^{k}(\hat x)} \\ \begin{aligned} \mathcal W_t \geq 0;\sum_{t=1}^{\mathcal T} \mathcal W_t = 1 \end{aligned} \end{cases} ⎩ ⎨ ⎧H(x^)=Ckargmax∑t=1TWt⋅htk(x^)Wt≥0;t=1∑TWt=1
回顾:明可夫斯基距离
在
K-Means
\text{K-Means}
K-Means算法中介绍过明科夫斯基距离
(
Minkowski Distance
)
(\text{Minkowski Distance})
(Minkowski Distance)。其是空间中两点
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)之间距离的一种描述:
Dist
m
k
(
x
(
i
)
,
x
(
j
)
)
=
[
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
m
]
1
m
\text{Dist}_{mk}(x^{(i)},x^{(j)}) = \left[\sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right|^m\right]^{\frac{1}{m}}
Distmk(x(i),x(j))=[k=1∑p
xk(i)−xk(j)
m]m1
其中
p
p
p表示样本点
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)随机变量/维度数量。当
m
=
1
m=1
m=1时的明可夫斯基距离为曼哈顿距离
(
Manhattan Distance
)
(\text{Manhattan Distance})
(Manhattan Distance)。也就是
L
1
L_1
L1范数:
Dist
m
a
n
(
x
(
i
)
,
x
(
j
)
)
=
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
\text{Dist}_{man}(x^{(i)},x^{(j)}) = \sum_{k=1}^p |x_k^{(i)} - x_k^{(j)}|
Distman(x(i),x(j))=k=1∑p∣xk(i)−xk(j)∣
同理,当
m
=
2
m=2
m=2时候的同理,当
m
=
2
m=2
m=2时的明可夫斯基距离为欧式距离
(
Euclidean Distance
)
(\text{Euclidean Distance})
(Euclidean Distance)。也就是
L
2
L_2
L2范数:
Dist
e
d
(
x
(
i
)
,
x
(
j
)
)
=
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
2
\text{Dist}_{ed}(x^{(i)},x^{(j)}) = \sqrt{\sum_{k=1}^p |x_k^{(i)} - x_k^{(j)}|^2}
Disted(x(i),x(j))=k=1∑p∣xk(i)−xk(j)∣2
K \mathcal K K近邻算法
算法描述
K \mathcal K K近邻 ( K-Nearest Neighbor algorithm,KNN ) (\text{K-Nearest Neighbor algorithm,KNN}) (K-Nearest Neighbor algorithm,KNN)是一种常用的监督学习方法。它的工作流程可表示为如下形式:
- 给定测试样本,以及训练数据集;
- 基于某种距离度量找出训练集内与其最接近的 K \mathcal K K个样本;
- 基于该
K
\mathcal K
K个样本的信息对测试样本进行预测:
关于不同任务,可以基于距离远近进行加权平均/加权投票。距离测试样本越近的样本点权重越大。- 如果是分类任务,关于测试样本的预测标签可使用投票法进行预测;
- 如果是回归任务,关于测试样本的预测标签可用平均法进行预测。即使用 K \mathcal K K个样本标签信息的均值作为测试样本的预测结果。
假设我们使用
K
\mathcal K
K近邻算法处理一个分类任务,见下图:

其中
x
t
e
s
t
x_{test}
xtest表示测试样本点;
分析过程中并没有使用‘加权投票’。
- 褐色圆表示 K = 1 \mathcal K =1 K=1时的判别范围。其中包含蓝色点 1 1 1个大于红色点 0 0 0个,最终测试样本点 x t e s t x_{test} xtest判别为蓝色;
- 黑色圆表示 K = 3 \mathcal K = 3 K=3时的判别范围。其中包含蓝色点 1 1 1个小于红色点 2 2 2个,最终测试样本点 x t e s t x_{test} xtest被判别为红色;
- 蓝色圆表示 K = 5 \mathcal K = 5 K=5时的判别范围。其中包含蓝色点 2 2 2个小于红色点 3 3 3个,最终测试样本点 x t e s t x_{test} xtest被判别为红色;
很显然,
K
\mathcal K
K是一个重要参数,当
K
\mathcal K
K取不同值时,我们关于测试样本点的判别结果有可能存在差异;同理,如果使用不同的距离计算方式,可能会找到不同的近邻结果,从而会影响最终的判别结果。
上述示例中使用欧式距离作为距离计算方式。
K \mathcal K K值的选择
K \mathcal K K值自身的意义在于满足某种距离计算方式的条件下,符合条件的样本数量。这意味着 K \mathcal K K是一个 > 0 >0 >0的整数:
- 如果选择较小的 K \mathcal K K值,这意味着选择样本的方式是局部的——只有与测试样本点最近似的 K \mathcal K K个样本点才会对预测结果起作用,这会出现:我们可能并没有对分布进行完整的认识,仅使用很小一部分子集对测试样本进行判别。这种做法会使得预测结果的偏差很小/很准确,但预测结果的方差很大(相同类别的测试样本可能因各自的小子集结果不同而产生不同的判别结果),从而容易发生过拟合 ( Over-Fitting ) (\text{Over-Fitting}) (Over-Fitting)现象。
- 相反,如果选择较大的 K \mathcal K K值,此时的选择样本的方式是宽泛的。如果 K \mathcal K K过大,会导致与测试样本点不相似 的其他样本点涵盖进来,从而对大范围的样本进行投票/均值。这会导致回归任务中,两个特征相差较大的样本点经过 K \mathcal K K值的平均操作,反而相差不大。这意味着预测结果的方差很小。从而容易发生欠拟合 ( Under-Fitting ) (\text{Under-Fitting}) (Under-Fitting)现象。
- 当 K \mathcal K K值大到极限,此时 K \mathcal K K等于样本点总数 N N N。以分类任务为例,每一次判别测试样本点的类别信息时,要将所有样本点放在一起去投票。由于训练集内的样本相对于真实分布是不完整的,而我们此时通过各类别样本数量多少来判别结果,这明显是不合理的。
小插曲:懒惰学习与急切学习
上面介绍了 K \mathcal K K近邻算法的执行过程。我们发现它和其他算法的不同之处在于—— K \mathcal K K近邻算法没有显式的训练过程/没有训练所谓的模型。直接是已知样本空间,将测试样本点放入样本空间中找到对应位置,通过最近的 K \mathcal K K个样本点判别测试样本点信息。
- 我们称这种训练代价为零,待收到测试样本后再进行处理的方式称作懒惰学习 ( Lazy Learning ) (\text{Lazy Learning}) (Lazy Learning);
- 相反,那些在训练阶段就对样本进行学习和处理的算法(如神经网络等),被称作急切学习 ( Eager Learning ) (\text{Eager Learning}) (Eager Learning)。
它们各自的特点也是十分明显的:
- 急切学习虽然在训练过程中耗费了时间进行训练,但在测试/决策过程中花费时间几乎为 0 0 0。此时消耗的内存空间也因训练时模型参数的固定而确定;
- 懒惰学习没有训练过程,但在决策过程消耗时间较长。就以 KNN \text{KNN} KNN自身为例。仅仅计算测试样本点最近的 K \mathcal K K个样本的信息,就需要对训练集内的所有样本点进行 距离计算和排序,决策时间较慢(时间复杂度较大),占用内存空间比较大。
KD \text{KD} KD树描述及示例
在懒惰学习部分,介绍了 KNN \text{KNN} KNN执行过程中的缺陷:训练集和测试样本点均已知的条件下,想要找到某种距离计算方式下最近的 K \mathcal K K个样本点,它的计算代价较高。
KD \text{KD} KD树( K-Dimension Tree,KD-Tree \text{K-Dimension Tree,KD-Tree} K-Dimension Tree,KD-Tree)则给出了一种对样本索引的方式。其底层逻辑就是将整个样本空间有层次地 进行划分,然后通过索引在特定空间寻找合适样本。
KD \text{KD} KD树是一棵平衡二叉树。这里通过示例对 KD \text{KD} KD树以及对应样本空间进行描述:
-
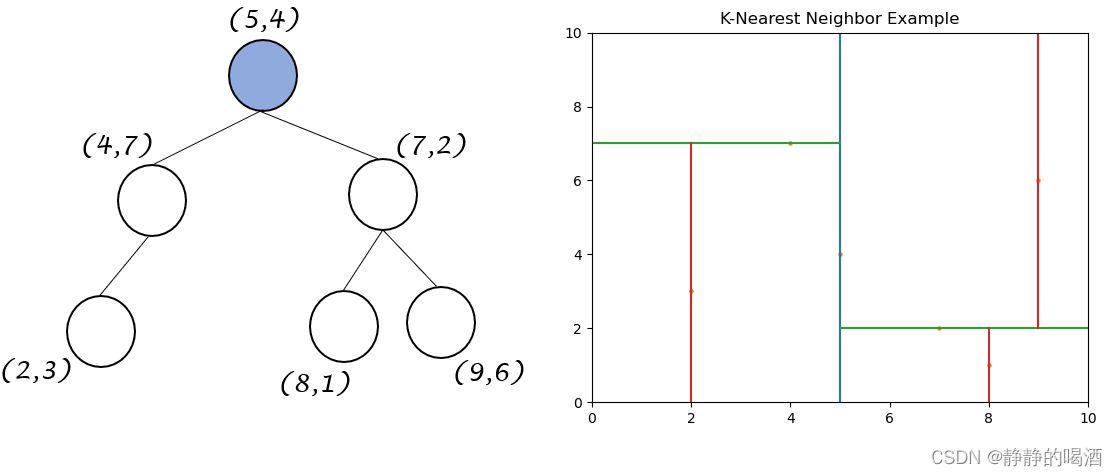
已知某二维样本空间包含 6 6 6个样本点 D = { ( 2 , 3 ) , ( 5 , 4 ) , ( 9 , 6 ) , ( 4 , 7 ) , ( 8 , 1 ) , ( 7 , 2 ) } \mathcal D = \{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\} D={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},其对应图像表示如下:

-
确定划分 ( Split ) (\text{Split}) (Split)域:基于当前样本两个维度的方差分别表示为: x : 5.81 , y : 4.47 x:5.81,y:4.47 x:5.81,y:4.47。 x x x维度的方差大这意味着沿着该维度方向进行数据分割能够获得最好的分辨率。最终选择 x x x维度(横坐标)作为划分域。
-
确定了划分域后,确定初始划分结点 ( Node-Data ) (\text{Node-Data}) (Node-Data):将样本点按照 x x x维度数值从小到大排序,位于中间的样本点被选择为 Node-Data \text{Node-Data} Node-Data。该数据集基于 x x x维度的排序结果表示如下:
[ ( 2 , 3 ) , ( 4 , 7 ) , ( 5 , 4 ) , ( 7 , 2 ) , ( 8 , 1 ) , ( 9 , 6 ) ] [(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)] [(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)]
这里中间样本点包含两个: ( 5 , 4 ) , ( 7 , 2 ) (5,4),(7,2) (5,4),(7,2),选择哪个都可以建树。这里以 ( 7 , 2 ) (7,2) (7,2)为 Node-Data \text{Node-Data} Node-Data示例。
一般情况下取上界。 -
将 ( 7 , 2 ) (7,2) (7,2)作为 KD \text{KD} KD树的根节点,并以 Node-Data \text{Node-Data} Node-Data的 x x x维度为界,对样本空间进行划分:

-
此时将样本空间划分为两个部分。各部分内部的样本点重复执行上述划分过程。再次以样本子集 { ( 2 , 3 ) , ( 4 , 7 ) , ( 5 , 4 ) } \{(2,3),(4,7),(5,4)\} {(2,3),(4,7),(5,4)}为例:
确定划分域: x : 1.56 , y : 2.89 x:1.56,y:2.89 x:1.56,y:2.89
确定划分结点: [ ( 2 , 3 ) , ( 5 , 4 ) , ( 4 , 7 ) ] ⇒ ( 5 , 4 ) [(2,3),(5,4),(4,7)] \Rightarrow (5,4) [(2,3),(5,4),(4,7)]⇒(5,4),并以其 y y y维度为界,对子空间进行划分:

-
以此类推,可得到最终划分结果以及对应 KD \text{KD} KD树以及 KD \text{KD} KD树表示如下:
相同颜色的划分边界对应KD \text{KD} KD树中的相同层。

同理。如果步骤1选择 ( 5 , 4 ) (5,4) (5,4)作为根结点,那么对应结果表示为:
K \mathcal K K近邻 VS \text{ VS } VS 贝叶斯最优分类器
这里观察 K \mathcal K K近邻算法与贝叶斯最优分类器关于错误率 ( Error Rate ) (\text{Error Rate}) (Error Rate)的描述,并比较它们直接按的大小关系。
这里假设距离度量得到的结果是有效的,并且仅以 K = 1 \mathcal K=1 K=1条件下在二分类问题错误率上的简单描述。
- 定义某测试样本
x
^
\hat x
x^,在
K
=
1
\mathcal K=1
K=1条件下的最近邻样本点是
Z
\mathcal Z
Z。这意味着,样本
x
^
\hat x
x^强行与
Z
\mathcal Z
Z的标签
C
\mathcal C
C相同:
从‘软投票’的角度观察,x ^ \hat x x^对于所有具体标签值的概率结果均与Z \mathcal Z Z相同。
P ( C ∣ x ^ ) = P ( C ∣ Z ) C ∈ Y \mathcal P(\mathcal C \mid \hat x) = \mathcal P(\mathcal C \mid \mathcal Z) \quad \mathcal C \in \mathcal Y P(C∣x^)=P(C∣Z)C∈Y - 那么对应的错误率表示为:
错误就意味着测试样本x ^ \hat x x^与样本Z \mathcal Z Z标记不同类别标签的概率。即1 − 1 - 1−它们标记相同标签的概率。
P ( e r r ) = 1 − ∑ C ∈ Y P ( C ∣ x ^ ) ⋅ P ( C ∣ Z ) \mathcal P(err) = 1 - \sum_{\mathcal C \in \mathcal Y} \mathcal P(\mathcal C \mid \hat x) \cdot \mathcal P(\mathcal C \mid \mathcal Z) P(err)=1−C∈Y∑P(C∣x^)⋅P(C∣Z) - 如果使用贝叶斯最优分类器来描述测试样本
x
^
\hat x
x^的最优标签结果
C
∗
\mathcal C^*
C∗,那么
C
∗
\mathcal C^*
C∗可表示为:
C ∗ = arg max C ∈ Y P ( C ∣ x ^ ) ⇔ P ( C ∗ ∣ x ^ ) = max C ∈ Y P ( C ∣ x ^ ) \mathcal C^* = \mathop{\arg\max}\limits_{\mathcal C \in \mathcal Y} \mathcal P(\mathcal C \mid \hat x) \Leftrightarrow \mathcal P(\mathcal C^* \mid \hat x) = \mathop{\max}\limits_{\mathcal C \in \mathcal Y} \mathcal P(\mathcal C \mid \hat x) C∗=C∈YargmaxP(C∣x^)⇔P(C∗∣x^)=C∈YmaxP(C∣x^) - 至此,
P
(
e
r
r
)
\mathcal P(err)
P(err)可表示为如下形式:首先将
P
(
C
∣
x
^
)
=
P
(
C
∣
Z
)
\mathcal P(\mathcal C \mid \hat x) = \mathcal P(\mathcal C \mid \mathcal Z)
P(C∣x^)=P(C∣Z)带入
P
(
e
r
r
)
\mathcal P(err)
P(err)中:
P ( e r r ) = 1 − ∑ C ∈ Y P ( C ∣ x ^ ) ⋅ P ( C ∣ Z ) = 1 − ∑ C ∈ Y [ P ( C ∣ x ^ ) ] 2 \begin{aligned} \mathcal P(err) & = 1 - \sum_{\mathcal C \in \mathcal Y} \mathcal P(\mathcal C \mid \hat x) \cdot \mathcal P(\mathcal C \mid \mathcal Z) \\ & = 1 - \sum_{\mathcal C \in \mathcal Y} \left[\mathcal P(\mathcal C \mid \hat x)\right]^2 \end{aligned} P(err)=1−C∈Y∑P(C∣x^)⋅P(C∣Z)=1−C∈Y∑[P(C∣x^)]2
关于 ∑ C ∈ Y [ P ( C ∣ x ^ ) ] 2 \sum_{\mathcal C \in \mathcal Y} \left[\mathcal P(\mathcal C \mid \hat x)\right]^2 ∑C∈Y[P(C∣x^)]2和 [ P ( C ∗ ∣ x ^ ) ] 2 \left[\mathcal P(\mathcal C^* \mid \hat x)\right]^2 [P(C∗∣x^)]2之间的大小关系。很明显, [ P ( C ∗ ∣ x ^ ) ] 2 \left[\mathcal P(\mathcal C^* \mid \hat x)\right]^2 [P(C∗∣x^)]2是 ∑ C ∈ Y [ P ( C ∣ x ^ ) ] 2 \sum_{\mathcal C \in \mathcal Y} \left[\mathcal P(\mathcal C \mid \hat x)\right]^2 ∑C∈Y[P(C∣x^)]2内的一项,自然 [ P ( C ∗ ∣ x ^ ) ] 2 ≤ ∑ C ∈ Y [ P ( C ∣ x ^ ) ] 2 \left[\mathcal P(\mathcal C^* \mid \hat x)\right]^2\leq\sum_{\mathcal C \in \mathcal Y} \left[\mathcal P(\mathcal C \mid \hat x)\right]^2 [P(C∗∣x^)]2≤∑C∈Y[P(C∣x^)]2。从而有:
P ( e r r ) ≤ 1 − [ P ( C ∗ ∣ x ^ ) ] 2 \mathcal P(err) \leq 1 - [\mathcal P(\mathcal C^* \mid \hat x)]^2 P(err)≤1−[P(C∗∣x^)]2
使用乘法分配律将其展开,其中 1 − P ( C ∗ ∣ x ^ ) 1 - \mathcal P(\mathcal C^* \mid \hat x) 1−P(C∗∣x^)表示贝叶斯最优分类器的错误率。且 P ( C ∗ ∣ x ^ ) ≤ 1 \mathcal P(\mathcal C^* \mid \hat x) \leq 1 P(C∗∣x^)≤1恒成立。因而有:
P ( e r r ) ≤ [ 1 + P ( C ∗ ∣ x ^ ) ] ⋅ [ 1 − P ( C ∗ ∣ x ^ ) ] ≤ 2 × [ 1 − P ( C ∗ ∣ x ^ ) ] \begin{aligned} \mathcal P(err) & \leq [1 + \mathcal P(\mathcal C^* \mid \hat x)] \cdot [1 - \mathcal P(\mathcal C^* \mid \hat x)] \\ & \leq 2 \times [1 - \mathcal P(\mathcal C^* \mid \hat x)] \end{aligned} P(err)≤[1+P(C∗∣x^)]⋅[1−P(C∗∣x^)]≤2×[1−P(C∗∣x^)]
这意味着 KNN \text{KNN} KNN的泛化错误率不超过贝叶斯最优分类器的两倍。
相关参考:
详细的
KNN
\text{KNN}
KNN算法原理步骤
一看就懂的K近邻算法(KNN),K-D树,并实现手写数字识别!
机器学习(周志华著)