学习目标:
如果要学习构造数值积分公式的基本方法与有关概念,可以遵循以下步骤:
1.了解数值积分的基本概念和性质:包括积分的定义、积分的性质、数值积分的定义及其误差等。这可以通过课本或相关的学习资料来了解。
2.掌握构造数值积分公式的基本方法:这包括插值法、拟合法、加权残差法等。
3.掌握构造数值积分公式的常用方法:包括矩形公式、梯形公式、辛普森公式等。
4.掌握数值积分误差的估计方法:这包括理论误差、实际误差的计算方法等。
5.练习题目并做好总结:通过做题目,巩固对数值积分的掌握,并且对容易出错的地方进行总结和反思。
总之,要学习构造数值积分公式的基本方法与有关概念,需要有一定的数学基础和数值计算的基础,需要认真学习并练习。

为什么有数值积分:
数值积分是指利用数值方法对给定的函数在一定区间内进行积分近似计算的方法。其主要应用于以下几个方面:
-
函数表达式较为复杂,难以求出解析积分式,只能通过数值积分来求近似值。
-
函数表达式虽然可以求出解析积分式,但是解析式求解比较困难或计算量很大,使用数值积分来近似计算更为方便和高效。
-
对于某些具体问题,需要对函数在一定区间内进行积分,但是区间很大或者积分精度要求很高,只能采用数值积分方法来求解。
总的来说,数值积分在实际应用中具有很广泛的应用,能够对科学计算、工程设计、金融分析等领域提供有力支持。

5.2.1 构造数值积分公式的基本方法
构造数值积分公式的基本方法包括以下步骤:
-
选取积分区间 [a,b],并将其分割成 n个子区间,长度为 h=(b-a)/n。
-
选择数值积分公式的节点和权重。常见的选择包括梯形公式、Simpson公式和Gauss-Legendre公式等。
-
在每个子区间上应用数值积分公式,计算出每个子区间的积分值。
-
将每个子区间的积分值相加,得到整个区间 [a,b]的数值积分值。
其中,节点和权重的选择是构造数值积分公式的关键。不同的数值积分公式选择不同的节点和权重,因此具有不同的精度和收敛性质。对于某些特殊的函数,如奇异函数或高度振荡函数,选择合适的节点和权重也是非常重要的。此外,积分区间的分割方法也会影响数值积分的精度和收敛性质。
 5.2.2 数值积分公式的余项
5.2.2 数值积分公式的余项
在数值积分中,我们使用数值方法来近似计算一个函数在给定区间上的积分值。构造数值积分公式的基本方法是通过对函数进行插值或逼近,然后用这个插值或逼近多项式的积分值来代替原函数在给定区间上的积分值。然而,由于实际上我们是用一个多项式来近似计算一个函数,所以得到的积分值通常只是一个近似值,而不是精确值。
为了评估数值积分公式的精确性,我们通常需要考虑其余项。余项指的是我们通过数值积分公式计算得到的近似积分值与真实积分值之间的差异。如果我们知道了余项的大小,就可以通过控制余项来提高数值积分的精确度。
余项的大小通常由被积函数在给定区间上的某些导数的最大值来决定。对于基于插值多项式的数值积分公式,通常使用插值多项式的误差公式来估计余项的大小。而对于基于高斯求积的数值积分公式,余项的大小通常由高斯积分公式的余项来决定。
总之,了解数值积分公式的余项可以帮助我们评估其精确性,并在需要时进行优化。

我的理解:
数值积分公式的余项是指数值积分公式与真实积分之间的误差。在实际问题中,我们通常无法求得精确的积分值,只能通过数值积分公式来近似求解。因此,了解数值积分公式的余项可以帮助我们评估数值积分的精度和可靠性,以及优化数值积分方法的选取。
余项可以通过泰勒展开或其他数学方法推导得到,通常表示为一个函数或者一个常数乘以某个幂次的步长。在实际应用中,我们可以通过控制步长和积分函数的光滑度等因素来控制余项的大小,从而提高数值积分的精度和可靠性。

5.2.3 数值积分公式的代数精度
在数值积分中,代数精度是用来衡量数值积分公式近似计算精度的一种指标。一个数值积分公式的代数精度是指该公式对于多项式函数的精确积分与其插值多项式的积分之差最高为多少次幂的误差。
具体来说,假设我们有一个n阶数值积分公式:
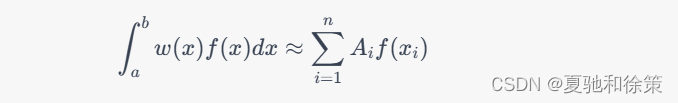
其中,w(x)是权函数,A_i是积分系数,x_i是积分节点。如果对于任意的n \geq 0,该数值积分公式在所有阶不超过n的多项式函数f(x)上都精确成立,即:
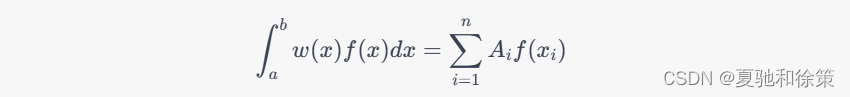
那么这个数值积分公式的代数精度就是n。
代数精度高的数值积分公式对于多项式函数的积分近似误差较小,因此在数值计算中更加精确。
总结:
构造数值积分公式的基本方法和有关概念涉及到以下重点和难点和易错点:
重点:
1.数值积分的基本思想是用一些离散点上的函数值来近似替代积分值。 2.常用的数值积分方法包括:牛顿-科茨公式、梯形公式、辛普森公式等。 3.数值积分公式的代数精度是指数值积分公式和被积函数在一定的代数精度下能够完全重合。 4.数值积分公式的余项表示代数精度未达到完全重合时的误差项。
难点:
1.数值积分公式的推导涉及到积分理论、泰勒公式等数学知识,需要掌握相关的数学基础知识。 2.在实际计算中,由于被积函数的特殊性质或者数值积分方法的限制,有时难以达到理论上的代数精度要求。 3.对于复杂函数的数值积分,需要考虑积分区间的划分、数值积分公式的选择等问题,难度较大。
易错点:
1.理解数值积分公式的代数精度和余项的概念及其区别。 2.在选择数值积分方法和积分区间的划分时,需要考虑被积函数的特性,选择合适的方法和划分,否则可能导致计算误差较大。 3.在计算时,需要注意舍入误差和截断误差的影响,避免误差积累导致计算结果的失真。