目录

1.代数推导

2.几何推导

3.总结

---

1.代数推导

假设我们有一个正方形初始边长为X，这时面积S1=x²

然后正方形的边长增加△x，此时面积S2=（x+△x）²

变化的面积大小是△s=（x+△x）²- x²=2x△x+（△x）²

观察可以发现当△x越小(△x)²会比2x△x率先趋近于0，也就是换句话说，当△x很小时我们可以近似的认为

△s=2x△x

仔细观察上面的式子，这个2X其实就是x的平方的导数，这时候我们是不是就理解了为什么说导数可以描述变化趋势的快慢。

2.几何推导

几何推导其实也是几何意义。

将就以上的函数做出图像，以此图像来理解微分的几何意义:

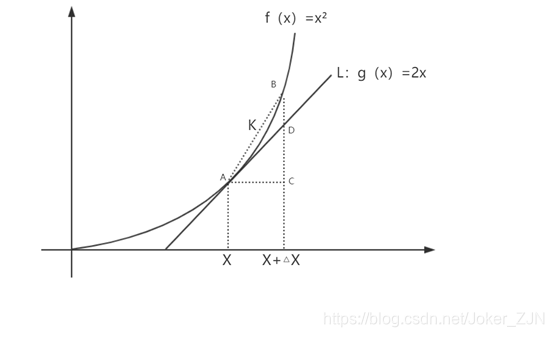
K:AB两点的连线

L：A点的切线

接下来计算△y：

         △y有两种计算方法：

         ①函数代值，末减初：

△y=(x+△x)²-x²=x²+2△x+（△x）²-x²

  =2x△x+(△x)²

         ②通过斜率计算：

                  ∵△y/△x=k

                  ∴△y=k△X

                  之前已经推导过x²的（导数）斜率是2x，

也就是说函数上每一点的斜率是随x变化的。

A处斜率为：2x

B处斜率为：2(x+△x)

观察图中的两条直线K、L：

K线斜率是x与x+△x两点间的斜率。

L线是A点的切线，L线的斜率是A点的斜率。

不管是观察图形也好，根据上面斜率的函数求证也好都可以看出：

                  当△x越小，x+△x越接近x点时：

                  K线和函数图形都无限趋近于L线，三者在A点处重合。

                  意味着什么？

意味着当△x足够小的时候L线可以代替函数图像和K线被用于计算，即A、B两点间的斜率可以近似等于A点的斜率，于是有：

                  △y=2X△X

总结以下上面通过两种方法求出两个△y：

         直接代值求出：

△y=2x△x+(△x)²

通过斜率求出：

△y=2X△X

可以发现直接代值求出的精确值和通过斜率趋近求出来的近似值之间的差距为：

△X²，当变化足够小，△X趋近于0时，△X²自然可以省略。

其实通过图像也可以严格的推导出△X²为0，可以省掉：

BC是直接代值对应的△y，

CD是用无限趋近得到的△y

BD段其实就是△X²

△X足够小，三线无限趋近，BC五险趋近于CD。BD无限趋近于0也就是说△X²无限趋近于0，所以自然可以省掉。

总结：

总结一下以上推导过程的最终结果：

f（X）,当△X->0：

△y=f’(X)△x

用一个符号d来代替△

         dy= f’(X)dx

         d称为微分符号。

（其实这里式子变形还可以证明出导数是微分的商——微商——f’(X)=dy/dx）

3.总结

总结一下微分到底是什么：

用人话来说就是——无限逼近，将一个大的东西切成足够微小的东西，这样一些没被分之前就很小的量就可以忽略不计，计算上关注大体而不拘泥于细节。

用不是人话的人话来说：

非线性函数的局部线性化，曲线的局部直线化。

稍微解释一下这句不是人话的人话：

三线无限逼近就已经可以看到是用切线函数这条直线来代替原本的曲线函数图像来用于计算，将原本非线性化的函数近似线性化。这在工程上很多不好计算的情景提出了解法。