本期介绍样本统计量是怎么算的,并用Python来模拟随机抽样。用一个在鱼塘捞鱼的简单例子来理解样本均值的概念。
如何理解重复试验?
指能够在完全相同条件下进行多次的试验;
比如我们抛10枚硬币,用来计算正面出现的概率,那每抛一次就相当于进行了一次试验,可以抛3次小样本,也可以抛30次大样本。
如何理解样本统计量?
每进行一次抽样,都能获得一个样本均值。也即每次抽样只能计算1次样本均值,有多少次抽样就有多少个样本均值。
比如我们要算鱼塘鱼的长度,在鱼塘随机捞10条鱼,计算鱼的平均长度,放回后又重新捞10条,那就相当于进行了两次试验,并且得到了2组样本均值。这计算得出的样本均值就是样本统计量啦。
接下来用Python模拟从鱼塘里捞鱼测量鱼的长度:
先调用要用到的包:
# 用于数值计算的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 用于绘图的库
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 设置浮点数打印精度
%precision 3
# 在Jupyter Notebook 里显示图形
%matplotlib inline定义一个总体:均值为4,标准差为0.8(方差为0.64)
population = stats.norm(loc = 4, scale = 0.8)代码详解:
scipy库中的norm函数用于创建正态分布概率密度函数;
loc参数指定正态分布的均值为4;
scale参数指定正态分布的标准差为0.8;
接下来用Python模拟一下随机试验和样本均值的计算:
sample_mean_array = np.zeros(10000)
np.random.seed(1)
for i in range(0, 10000):
sample = population.rvs(size = 10)
sample_mean_array[i] = sp.mean(sample)zeros()函数创建了一个长度为10000的一维数组,并将其所有元素都初始化为0,用于存储多次随机抽样后的样本均值;
random是随机函数,seed是随机种子,设置随机种子可以保证每次随机数生成的结果都是相同的;
for循环设置一个0到10000的循环;
population指正态分布概率密度函数对象;rvs方法是random variates方法的缩写,用于生成符合指定分布的随机变量; 也可以这样写:stats.norm.rvs(loc = 4, scale =0.8, size = 10);
mean()求均值,得到每次试验的样本均值,并保存在sample_mean_array里;
最后计算这10000次试验的均值,结果与总体均值很接近:
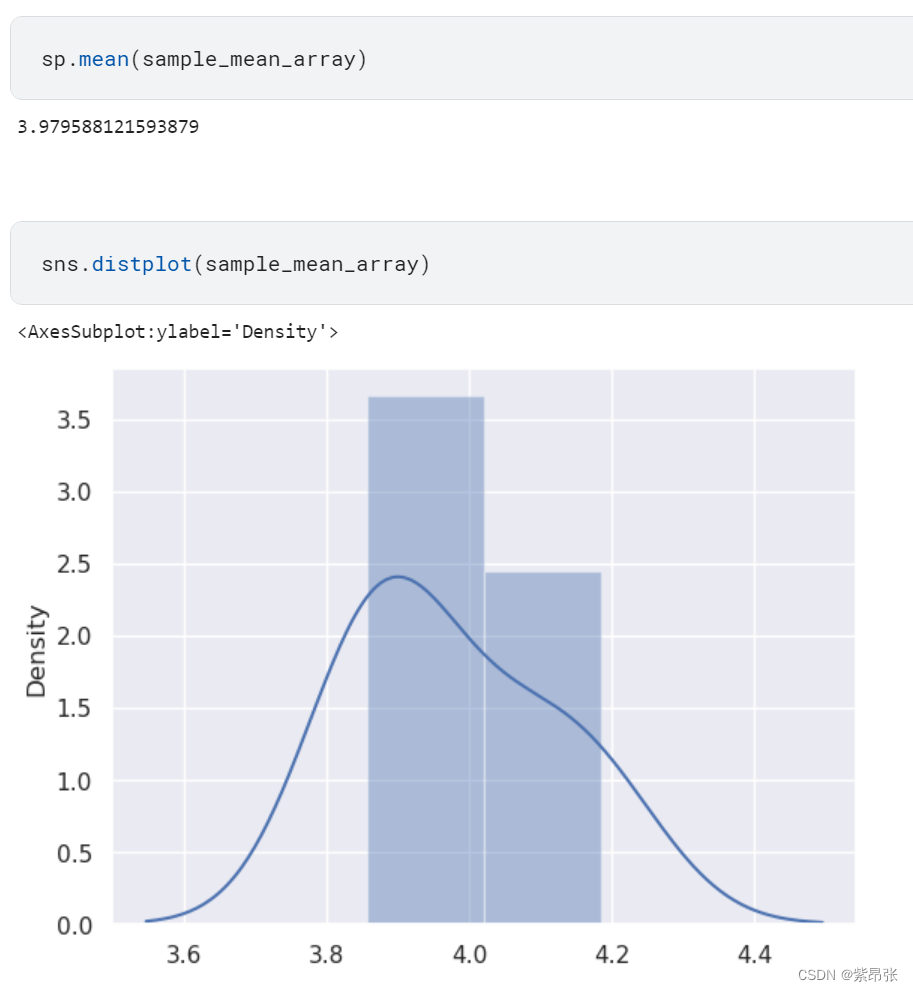
sp.mean(sample_mean_array)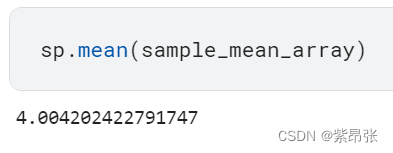
绘制样本均值的直方图,也是近似正态分布:
sns.distplot(sample_mean_array)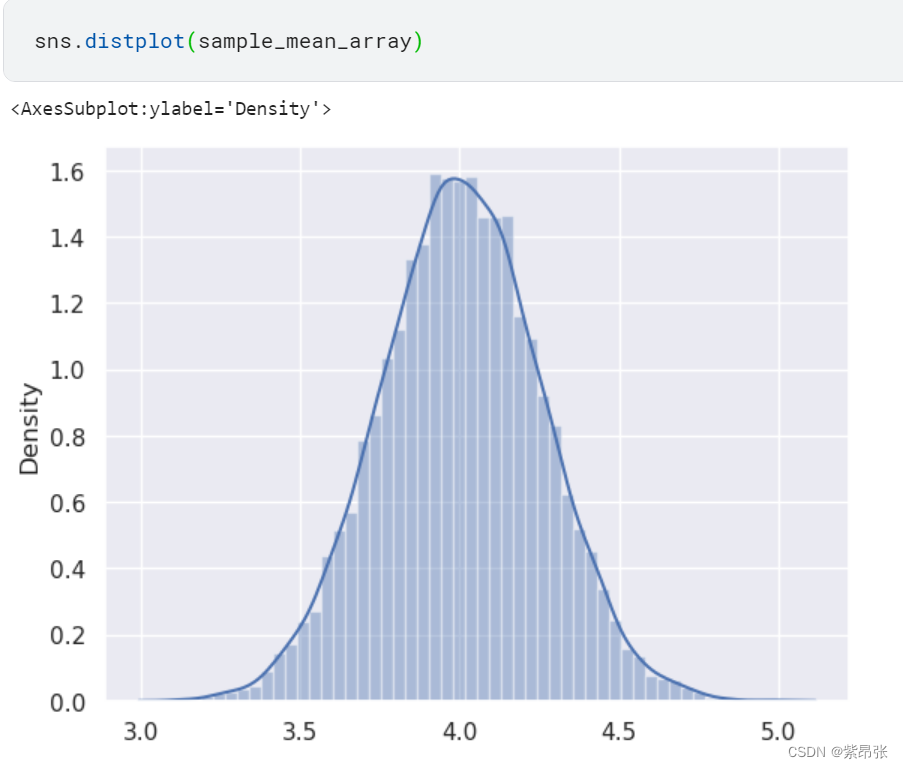
如果只进行5次试验,结果可见样本均值比总体均值的差距就稍微有点大了: