比特行列置乱加密

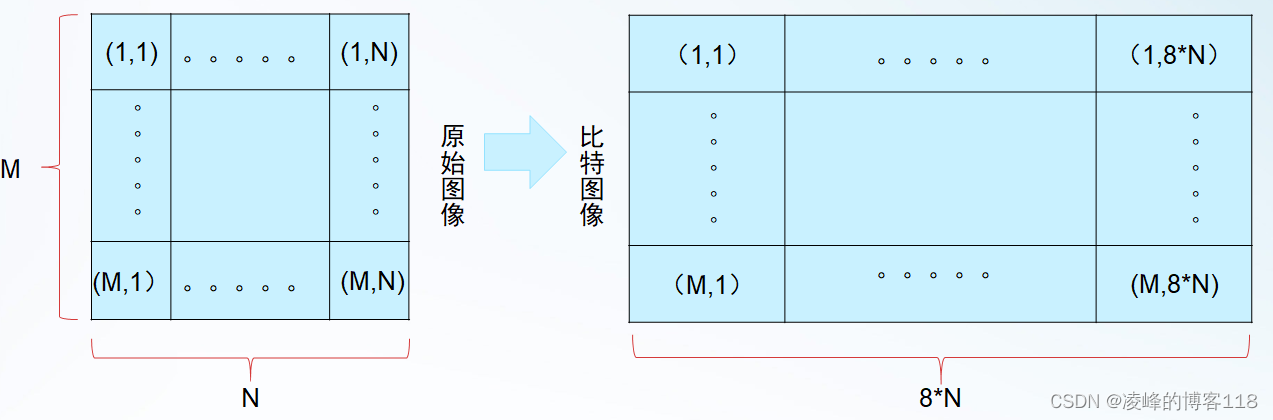
将M×N大小的灰度图像每个像素值转换为8bit二进制，得到M×8N大小的二值图像。
基于加密秘钥，生成随机序列TM和TN分别对二进制图像的行列进行置乱，生成置乱加密后的图像。

Logistic混沌序列加密：

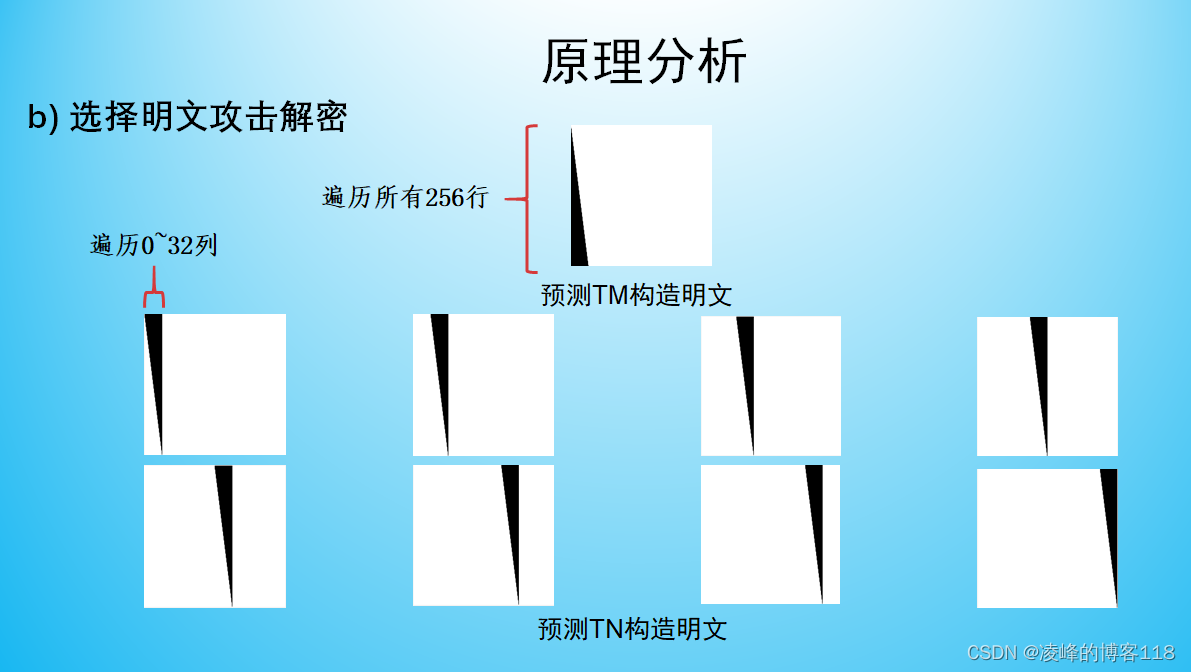
选择明文攻击过程

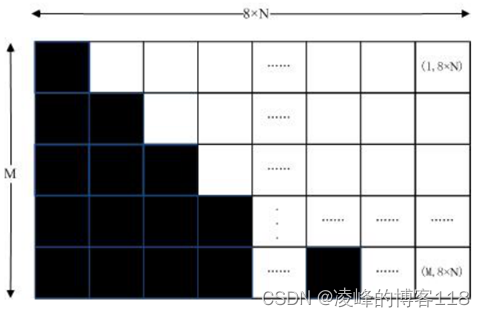
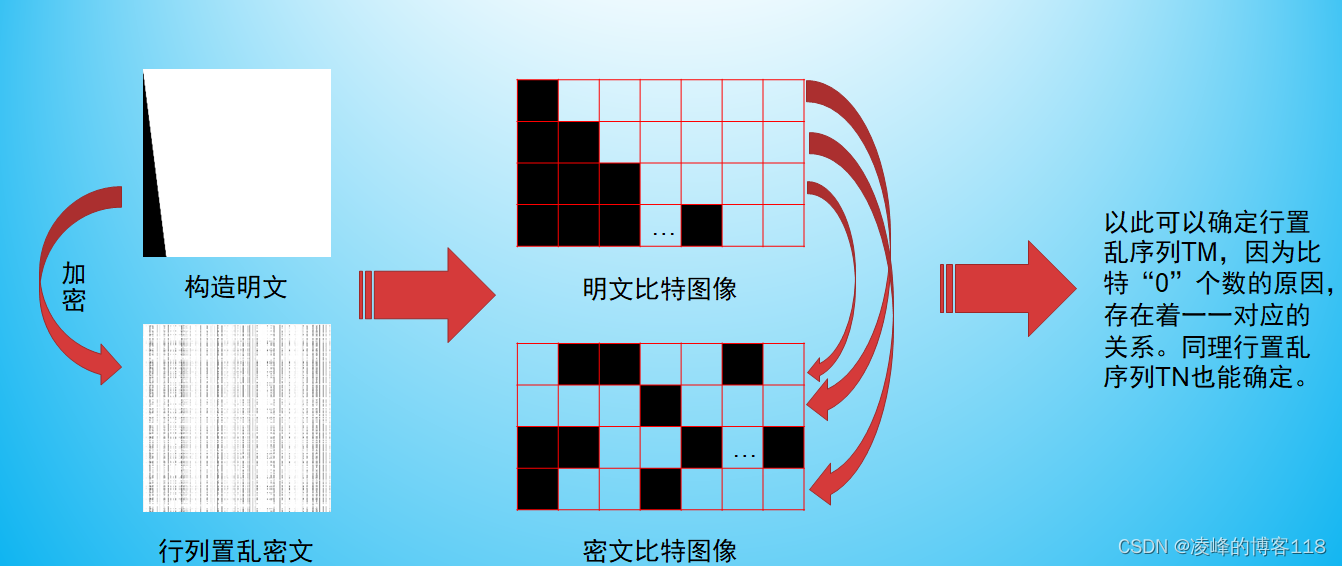
文献【2】与文献【1】主要内容有了攻击方法的不同，文献【2】采用选择明文攻击，用了9张构造的特殊图像进行加密后攻击，利用图像的特殊特性可以有效的预测得到原始密钥。下图是在对行置乱序列TM进行预测所构造的明文的过程，将比特化后的白色图像每一行的某几位比特进行“0”赋值，例如第一行赋一个比特为“0”，第二行赋两个比特为“0”，以此类推。原则是明了每行“0”的个数，并且遍历每行。

1.构造明文

下图是选择明文攻击构造的9张明文：

对构造的明文进行行列置乱加密并估计置乱秘钥

下图为将构造的明文行列置乱加密后得到的密文。利用构造的明文和对应的密文估计置乱秘钥。

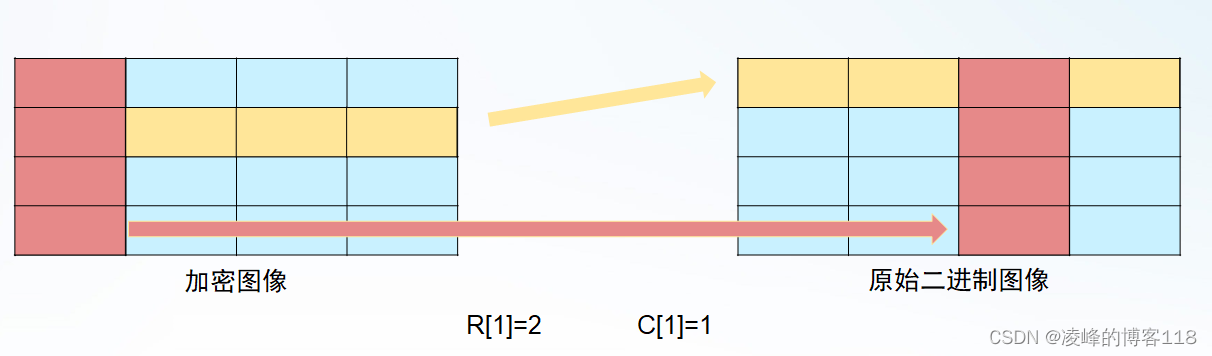
步骤1：比较原始比特图像和加密图像每一行“1”的个数，把只有唯一“1”个数的行下标记录在集合R中。
步骤2：如同步骤1，比较原始比特图像和加密图像每列“1”的个数，并把唯一“1”个数列下标记录在集合C中。

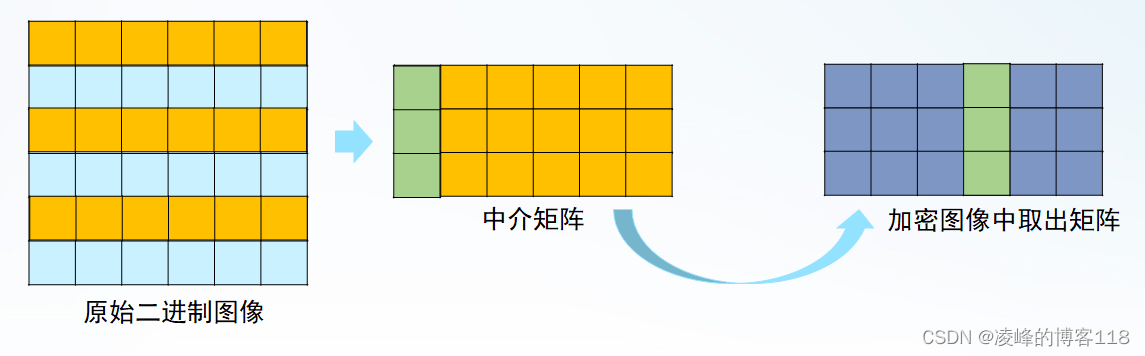
步骤3：取出原始比特矩阵中有唯一“1”个数的行，构成一个中介矩阵，把该矩阵和从加密矩阵中取出所对应R集序号的矩阵进行比较，把加密矩阵完全相同的列数存入集合C。
步骤4：同3，取出原始比特矩阵中唯一“1”个数的列，构成一个中介矩阵，把该矩阵和从加密矩阵中取出所对应C集序号的矩阵进行比较，把加密矩阵完全相同的行数存入集合R。

步骤5：由于上述1234步每次取都是取唯一相同的行或列，只操作一轮矩阵中肯定存在其余无法确定的行和列，因为存在有若干行列“1”的个数会相同。 比如：1、2步有相同“1”的个数的行列；3、4步对于R\C有相同的行列。 所以第5步需要重复3步和第4步，直到集合R、C不再增加，即可得到加密置乱矩阵。

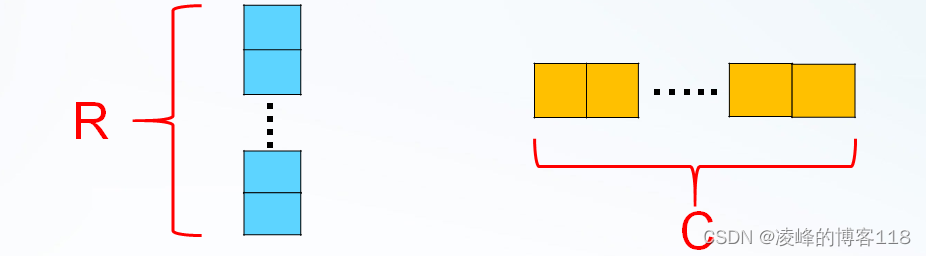
利用该算法，在对加密图像进行已知明文攻击时，所需要的明文密文对不需太多，并且效果较好

实验结果

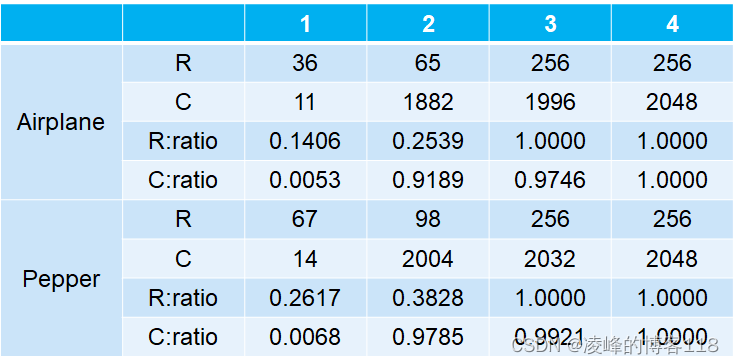
下表表示了文献【1】分别用airplane、pepper图对baboob进行攻击每一步后R、C得到的正确行列长度，并且计算了在此时其与最大行列的比率，也即表示预测正确率。结论：对R进行预测时，往往在第3步时就能得到所有正确置乱序号。对C进行预测时，由于列数多，第一步正确率较少，但在第二步就能得到大部分正确序号。

文献【1】、【2】中介绍的行列置乱加密图像和随机置乱加密图像比较，有明显的图像特征，因此有较大的安全隐患。

结论

对于行列置乱，无论在最初TM,TN迭代多少次，本质上都只是矩阵的变换：

其安全性并不会随着迭代次数增多而增强…因此通过将行列置乱通过【3】可知，无论是仅仅只对像素进行该置乱，还是将图像比特化后进行该置乱，该加密方案并不是一个较安全的方案。

参考文献：

【1】Li C , Lin D , Lü, Jinhu. Cryptanalyzing an Image-Scrambling Encryption Algorithm of Pixel Bits[J]. IEEE Multimedia, 2016, 24(3):64-71.
【2】Zhao L , Adhikari A , Xiao D , et al. Cryptanalysis on an Image Scrambling Encryption Scheme Based on Pixel Bit[C]// Digital Watermarking - 9th International Workshop, IWDW 2010, Seoul, Korea, October 1-3, 2010, Revised Selected Papers. Springer-Verlag, 2010.
【3】 Li, Shujun , et al. “A general quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks.” Signal Processing: 23.3(2008):212-223.