一、说明
数据可视化需要显示种种数据,matplotlib负责曲线类画图,然而类似于图论的操作用什么方法。这里用networkx程序包完成。本文专门介绍这种程序包的用法。
二、生成图(Creating a graph)
2.1 创建一个没有节点和边的空图。
import networkx as nx
G = nx.Graph()注释
根据定义,图是节点(顶点)以及已识别的节点对(称为边、链接等)的集合。在 NetworkX 中,节点可以是任何可哈希对象,例如文本字符串、图像、XML 对象、另一个图形、自定义节点对象等。
Python 的 None 对象不应用作节点,因为它确定是否已在许多函数中分配可选函数参数。
2.2 在空图追加节点
图 G 可以通过多种方式增长。 NetworkX 包括许多图形生成器函数和设施,用于以多种格式读取和写入图形。开始之前,我们先看看简单的操作。
- 您可以一次添加一个节点,
G.add_node(1)示例1: 追加节点
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
G.add_node(1)
G.add_node(2)
G.add_node(3)
nx.draw(G, node_color='green')
plt.show()
- 添加节点列表
G.add_nodes_from([2, 3])示例2: 追加节点
# import required module
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
G.add_nodes_from([0,1,2, 3,4])
nx.draw(G, node_color='green')
plt.show()
- 或添加任何 nbunch 节点。 nbunch 是节点的任何可迭代容器,它本身不是图中的节点。 (例如列表、集合、图形、文件等。)
H = nx.path_graph(10)
G.add_nodes_from(H)示例3:
# import required module
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
# G.add_nodes_from([0,1,2, 3,4])
H = nx.path_graph(10)
G.add_nodes_from(H)
nx.draw(G, node_color='green')
plt.show()
请注意,G 现在包含 H 的节点作为 G 的节点。相比之下,您可以使用图 H 作为 G 中的节点。
>>> G.add_node(H)
图 G 现在包含 H 作为节点。这种灵活性非常强大,因为它允许图形的图形、文件的图形、函数的图形等等。值得考虑如何构建应用程序以使节点成为有用的实体。当然,您始终可以在 G 中使用唯一标识符,并且如果您愿意,可以使用一个单独的字典将标识符键入节点信息。
2.3 追加边(Edges)
- G 也可以通过一次添加一条边来增长,
>>> G.add_edge(1, 2)
>>> e = (2, 3)
>>> G.add_edge(*e) # unpack edge tuple*通过添加边列表。
G.add_edges_from([(1, 2), (1, 3)])
示例:
# import required module
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
# G.add_nodes_from([0,1,2, 3,4])
H = nx.path_graph(10)
G.add_nodes_from(H)
G.add_edges_from([(1, 2), (1, 3)])
nx.draw(G, node_color='green')
plt.show()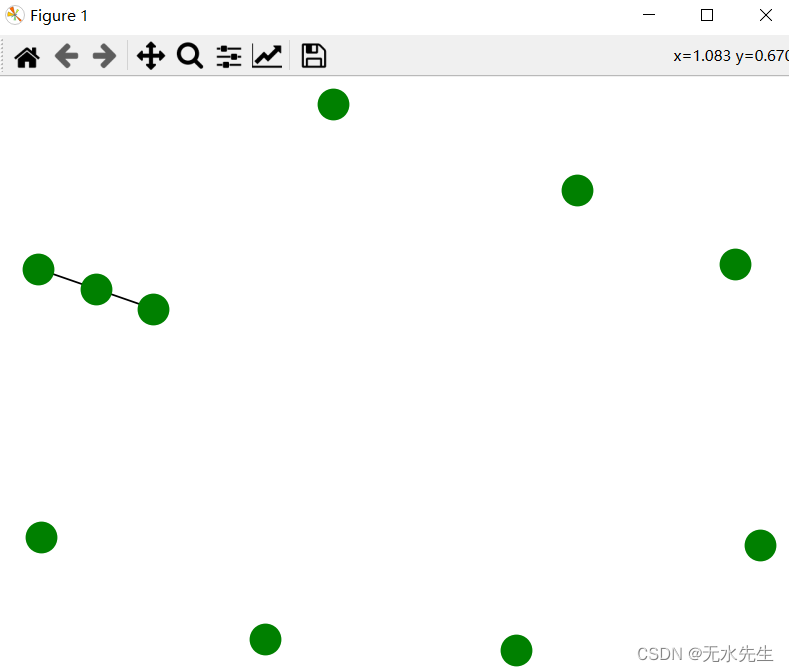
或通过添加任何 ebunch 边。 ebunch 是边元组的任何可迭代容器。边元组可以是节点的 2 元组或具有 2 个节点的 3 元组,后跟边属性字典,例如,(2, 3, {'weight': 3.1415})。边缘属性将在下面进一步讨论
>>> G.add_edges_from(H.edges())
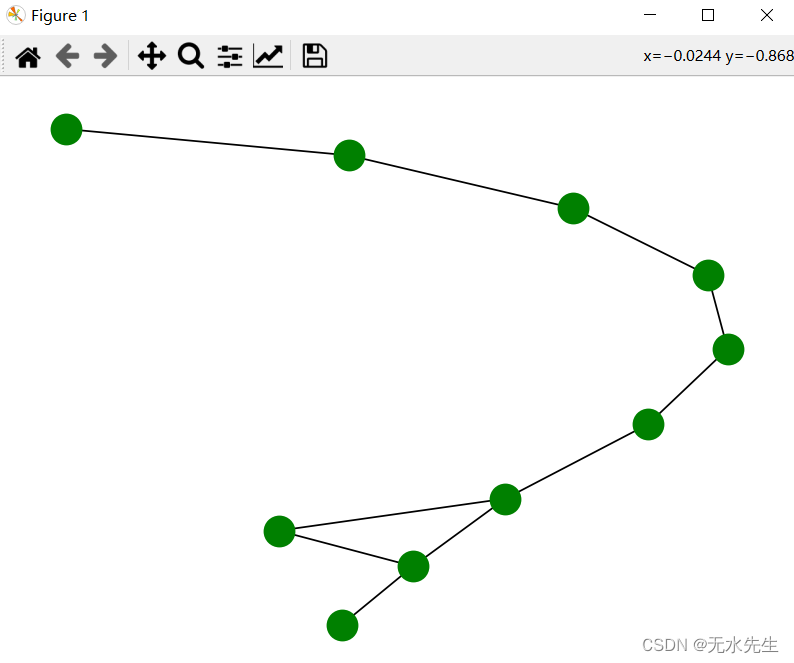
2.4 删除节点
人们可以用类似的方式拆除图表;使用 Graph.remove_node()、Graph.remove_nodes_from()、Graph.remove_edge() 和 Graph.remove_edges_from(),例如
G.remove_node(H)
添加现有节点或边缘时没有任何抱怨。例如,删除所有节点和边后
>>> G.clear()
我们添加新的节点/边,NetworkX 悄悄地忽略任何已经存在的。
>>> G.add_edges_from([(1, 2), (1, 3)])
>>> G.add_node(1)
>>> G.add_edge(1, 2)
>>> G.add_node("spam") # adds node "spam"
>>> G.add_nodes_from("spam") # adds 4 nodes: 's', 'p', 'a', 'm'
2.5 查询
在此阶段,图 G 由 8 个节点和 2 条边组成,如下所示:
>>> G.number_of_nodes() 8 >>> G.number_of_edges() 2
我们可以检查节点和边。这些方法返回节点、边、邻居等的迭代器。这通常可以提高内存效率,但这确实意味着我们需要指定将对象放入的容器类型。这里我们使用列表、集合、字典、元组和其他容器在其他情况下可能更好。
>>> list(G.nodes()) ['a', 1, 2, 3, 'spam', 'm', 'p', 's'] >>> list(G.edges()) [(1, 2), (1, 3)] >>> list(G.neighbors(1)) [2, 3]
删除节点或边的语法与添加类似:
>>> G.remove_nodes_from("spam")
>>> list(G.nodes())
[1, 2, 3, 'spam']
>>> G.remove_edge(1, 3)
通过实例化其中一个图形类来创建图形结构时,您可以指定多种格式的数据。
>>> H=nx.DiGraph(G) # create a DiGraph using the connections from G
>>> list(H.edges())
[(1, 2), (2, 1)]
>>> edgelist=[(0, 1), (1, 2), (2, 3)]
>>> H=nx.Graph(edgelist)
三、使用图内节点和边(nodes and edges)
您可能会注意到节点和边未指定为 NetworkX 对象。这使您可以自由地使用有意义的项目作为节点和边缘。最常见的选择是数字或字符串,但节点可以是任何可哈希对象(None 除外),并且边可以使用 G.add_edge(n1, n2, object=x) 与任何对象 x 相关联。
例如,n1 和 n2 可能是来自 RCSB 蛋白质数据库的蛋白质对象,x 可能指的是一份 XML 出版物记录,详细描述了它们相互作用的实验观察结果。
我们发现这种能力非常有用,但除非熟悉 Python,否则滥用它可能会导致意想不到的意外。如有疑问,请考虑使用 convert_node_labels_to_integers() 来获得更传统的带有整数标签的图。
3.1 访问边(edges)
除了 Graph.nodes()、Graph.edges() 和 Graph.neighbors() 方法之外,还可以使用下标表示法快速直接访问图形数据结构。
警告:不要更改返回的字典——它是图形数据结构的一部分,直接操作可能会使图形处于不一致的状态。
>>> G[1] # Warning: do not change the resulting dict
{2: {}}
>>> G[1][2]
{}
如果边已经存在,您可以使用下标符号安全地设置边的属性。
>>> G.add_edge(1, 3) >>> G[1][3]['color'] = "blue"
使用邻接迭代器可以快速检查所有边。请注意,对于无向图,这实际上会查看每条边两次。
>>> FG = nx.Graph()
>>> FG.add_weighted_edges_from([(1, 2, 0.125), (1, 3, 0.75), (2, 4, 1.2), (3, 4, 0.375)])
>>> for n, nbrs in FG.adjacency():
... for nbr, eattr in nbrs.items():
... data = eattr['weight']
... if data < 0.5: print('(%d, %d, %.3f)' % (n, nbr, data))
(1, 2, 0.125)
(2, 1, 0.125)
(3, 4, 0.375)
(4, 3, 0.375)
使用 edges 方法可以方便地访问所有边。
>>> for (u, v, d) in FG.edges(data='weight'):
... if d < 0.5: print('(%d, %d, %.3f)' % (u, v, d))
(1, 2, 0.125)
(3, 4, 0.375)
3.2 给图节点边 graphs, nodes, and edges加属性
权重、标签、颜色或您喜欢的任何 Python 对象等属性都可以附加到图形、节点或边上。
每个图、节点和边都可以在关联的属性字典中保存键/值属性对(键必须是可散列的)。默认情况下,这些是空的,但可以使用 add_edge、add_node 或直接操作名为 G.graph、G.node 和 G.edge 的属性字典来添加或更改图 G 的属性。
3.2.1 给图加属性(Graph attributes)
创建新图时分配图属性
>>> G = nx.Graph(day="Friday")
>>> G.graph
{'day': 'Friday'}
或者您可以稍后修改属性
>>> G.graph['day'] = "Monday"
>>> G.graph
{'day': 'Monday'}
3.2.2 节点属性(Node attributes)
使用 add_node()、add_nodes_from() 或 G.node 添加节点属性
>>> G.add_node(1, time='5pm')
>>> G.add_nodes_from([3], time='2pm')
>>> G.node[1]
{'time': '5pm'}
>>> G.node[1]['room'] = 714
>>> list(G.nodes(data=True))
[(1, {'room': 714, 'time': '5pm'}), (3, {'time': '2pm'})]
请注意,将节点添加到 G.node 不会将其添加到图中,请使用 G.add_node() 添加新节点。
3.2.3 节点属性Edge Attributes
使用 add_edge()、add_edges_from()、下标符号或 G.edge 添加边缘属性。
>>> G.add_edge(1, 2, weight=4.7 )
>>> G.add_edges_from([(3, 4), (4, 5)], color='red')
>>> G.add_edges_from([(1, 2, {'color': 'blue'}), (2, 3, {'weight': 8})])
>>> G[1][2]['weight'] = 4.7
>>> G.edge[1][2]['weight'] = 4
特殊属性 weight 应该是数字,并保存需要加权边的算法使用的值。
警告: 不要为 G.edge[u] 或 G.edge[u][v] 分配任何东西,因为它会破坏图形数据结构。如上所示更改边缘字典。
四、多种有向图
4.1 有向图Directed graphs
无向图和有向图唯一区别是:在生成图的时候可以选择Graph和DiGraph。
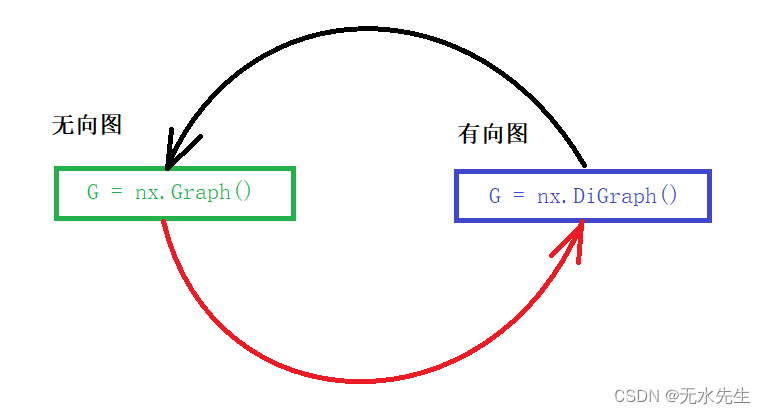
DiGraph 类提供了特定于有向边的其他方法,例如,
- DiGraph.out_edges()
- DiGraph.in_degree()
- DiGraph.predecessors()
- DiGraph.successors()
为了让算法轻松地与这两个类一起工作,有向neighbors() 和 degree() 的版本分别等同于 successors() 以及 in_degree() 和 out_degree() 的总和,尽管有时感觉不一致。
>>> DG = nx.DiGraph() >>> DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)]) >>> DG.out_degree(1, weight='weight') 0.5 >>> DG.degree(1, weight='weight') 1.25 >>> DG.successors(1) [2] >>> DG.neighbors(1) [2]
一些算法仅适用于有向图,而其他算法则没有为有向图很好地定义。事实上,将有向图和无向图混为一谈的趋势是危险的。如果您想将有向图视为无向图以进行某些测量,您应该使用 Graph.to_undirected() 或
H = nx.Graph(G) # convert G to undirected graph
4.2 多向图(Multigraphs)
允许有向图有双向边,就是多向图。
NetworkX 为图提供类,允许任意一对节点之间存在多条边。 MultiGraph 和 MultiDiGraph 类允许您添加相同的边两次,可能使用不同的边数据。这对于某些应用程序来说可能很强大,但许多算法在此类图形上的定义并不明确。在结果定义明确的情况下,例如 MultiGraph.degree() 我们提供该函数。否则,您应该以明确定义测量的方式转换为标准图形。
>>> MG = nx.MultiGraph()
>>> MG.add_weighted_edges_from([(1, 2, 0.5), (1, 2, 0.75), (2, 3, 0.5)])
>>> dict(MG.degree(weight='weight'))
{1: 1.25, 2: 1.75, 3: 0.5}
>>> GG = nx.Graph()
>>> for n, nbrs in MG.adjacency_iter():
... for nbr, edict in nbrs.items():
... minvalue = min([d['weight'] for d in edict.values()])
... GG.add_edge(n, nbr, weight = minvalue)
...
>>> nx.shortest_path(GG, 1, 3)
[1, 2, 3]
五、图生成和图操作(generators and graph operations)
除了逐个节点或逐条边构建图外,它们还可以通过以下方式生成
-
应用经典的图形操作,例如:
subgraph(G, nbunch) - induce subgraph of G on nodes in nbunch union(G1,G2) - graph union disjoint_union(G1,G2) - graph union assuming all nodes are different cartesian_product(G1,G2) - return Cartesian product graph compose(G1,G2) - combine graphs identifying nodes common to both complement(G) - graph complement create_empty_copy(G) - return an empty copy of the same graph class convert_to_undirected(G) - return an undirected representation of G convert_to_directed(G) - return a directed representation of G
-
使用对经典小图之一的调用,例如,
>>> peterseni = nx.petersen_graph() >>> tutte = nx.tutte_graph() >>> maze = nx.sedgewick_maze_graph() >>> tet = nx.tetrahedral_graph()
3. 对经典图使用(建设性的)生成器,例如.,
>>> K_5 = nx.complete_graph(5) >>> K_3_5 = nx.complete_bipartite_graph(3, 5) >>> barbell = nx.barbell_graph(10, 10) >>> lollipop = nx.lollipop_graph(10, 20)
4. 使用随机图形生成器,例如,
>>> er = nx.erdos_renyi_graph(100, 0.15) >>> ws = nx.watts_strogatz_graph(30, 3, 0.1) >>> ba = nx.barabasi_albert_graph(100, 5) >>> red = nx.random_lobster(100, 0.9, 0.9)
5. 使用常见的图形格式读取存储在文件中的图形,例如边列表、邻接列表、GML、GraphML、pickle、LEDA 等。
>>> nx.write_gml(red, "path.to.file")
>>> mygraph = nx.read_gml("path.to.file")
参考1: Reading and writing graphs
参考2: Graph generators
六、图论函数分析Analyzing graphs
G 的结构可以使用各种图论函数进行分析,例如:
>> G = nx.Graph()
>>> G.add_edges_from([(1, 2), (1, 3)])
>>> G.add_node("spam") # adds node "spam"
>>> list(nx.connected_components(G))
[{1, 2, 3}, {'spam'}]
>>> sorted(d for n, d in G.degree())
[0, 1, 1, 2]
>>> nx.clustering(G)
{1: 0.0, 2: 0.0, 3: 0.0, 'spam': 0.0}
返回节点属性的函数返回节点上的迭代器,值 2 元组。如果您愿意,这些可以很容易地存储在字典结构中。
>>> dict(nx.degree(G))
{1: 2, 2: 1, 3: 1, 'spam': 0}
对于特定节点的值,您可以提供单个节点或 nbunch 节点作为参数。如果指定单个节点,则返回单个值。如果指定了 nbunch,则该函数将返回一个字典。
>>> nx.degree(G, 1)
2
>>> G.degree(1)
2
>>> dict(G.degree([1, 2]))
{1: 2, 2: 1}
>>> sorted(d for n, d in G.degree([1, 2]))
[1, 2]
>>> sorted(d for n, d in G.degree())
[0, 1, 1, 2]s
算法 Algorithms
资料: Algorithms
七 画图函数Drawing graphs
NetworkX 主要不是图形绘制包,而是包括使用 Matplotlib 的基本绘图以及使用开源 Graphviz 软件包的界面。这些是 networkx.drawing 模块的一部分,如果可能将被导入。有关详细信息,请参阅绘图。
首先导入Matplotlib的plot接口(pylab也行)
>>> import matplotlib.pyplot as plt
您可能会发现使用“ipython -pylab”交互式测试代码很有用,它结合了 ipython 和 matplotlib 的强大功能,并提供了一种方便的交互模式。 要测试 networkx.drawing 的导入是否成功,请使用以下方法之一绘制 G
>>> nx.draw(G) >>> nx.draw_random(G) >>> nx.draw_circular(G) >>> nx.draw_spectral(G)
绘制到交互式显示器时。请注意,您可能需要发布一个 Matplotlib
>>> plt.show()
如果您不在交互模式下使用 matplotlib,则命令:(请参阅 Matplotlib 常见问题解答)
要将图纸保存到文件,请使用,例如
>>> nx.draw(G)
>>> plt.savefig("path.png")
写入本地目录中的文件“path.png”。如果 Graphviz 和 PyGraphviz 或 pydot 在您的系统上可用,您还可以使用 nx_agraph.graphviz_layout(G) 或 nx_pydot.graphviz_layout(G) 来获取节点位置,或以点格式编写图形以进行进一步处理。
>>> pos = nx.nx_agraph.graphviz_layout(G)
>>> nx.draw(G, pos=pos)
>>> nx.write_dot(G,'file.dot')
参考graphs: Drawing
import networkx
import matplotlib.pyplot as plt
# create object
G = networkx.lollipop_graph(5, 3)
# illustrate graph
networkx.draw(G, node_color='green')
plt.show()结果:
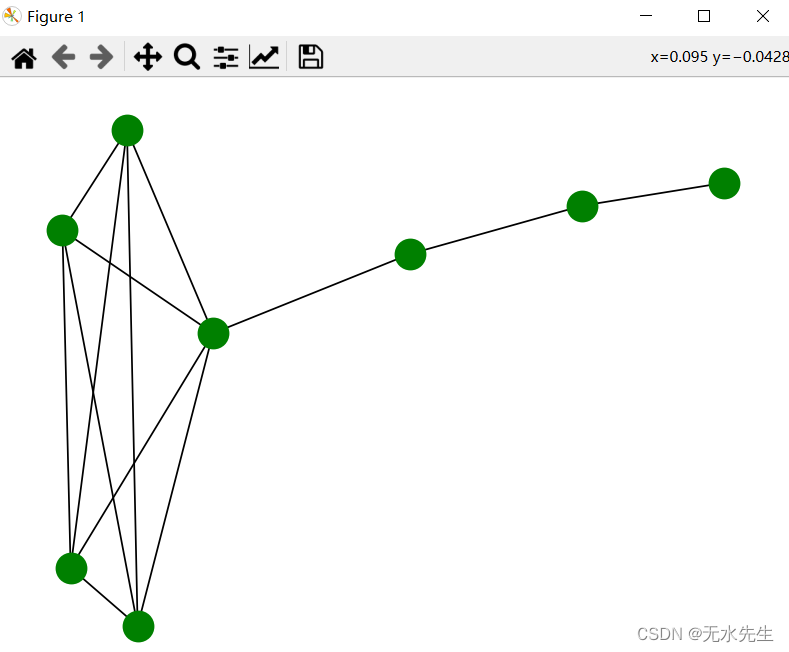
- lollipop_graph是棒糖图的函数
- G = networkx.lollipop_graph(5, 3) 该语句生成一个图,
- 全连接的是5个节点,3个节点是单联图。节点总数是8.
- 显示的时候节点位置是随机的。
Graph | NetworkX 入门教程 - 知乎 (zhihu.com)