题目来源：https://leetcode.cn/problems/rectangle-area/

---

矩形面积

题目介绍

给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其 左下 顶点和 右上 顶点坐标表示：

• 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。
• 第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。

示例1：

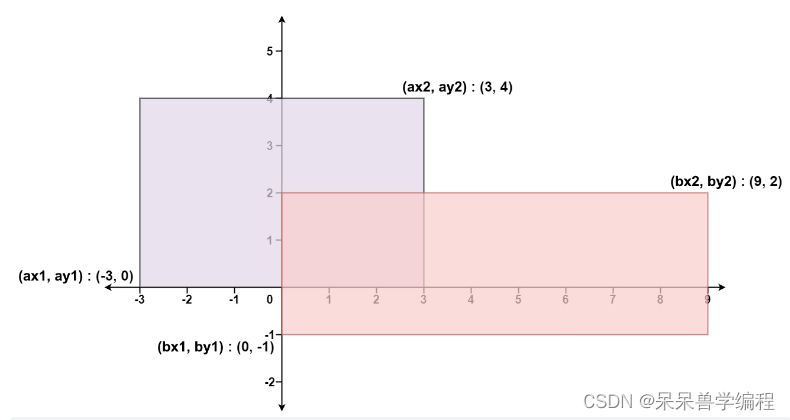
输入: ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出: 45
解释: 最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例1：

输入: ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出: 16

思路：
这是一道偏数学几何的编程题，题目给定两个矩形，要求返回覆盖总面积，所以需要考虑以下几种情况：

1. 两个矩形相交，总覆盖面积=矩形1+矩形2-重叠面积
   
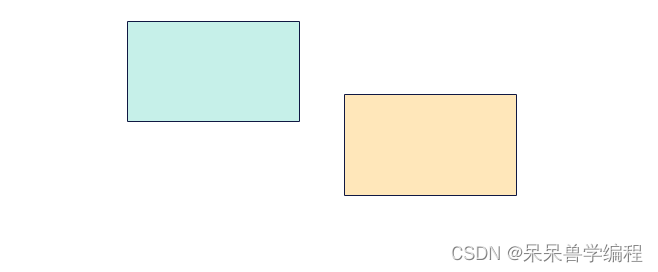
2. 两个矩形相交，总覆盖面积=矩形1+矩形2
   
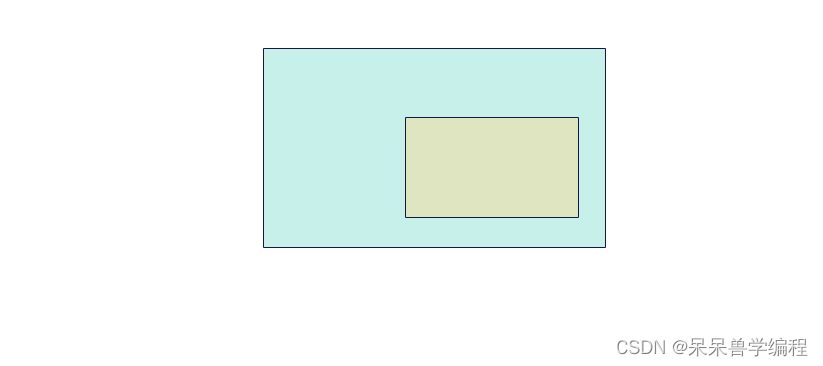
3. 大矩形包含小矩形，总覆盖面积=max(矩形1, 矩形2)
   

可以发现，有三种情况，有三个公式，所以说每次都需要判断三种情况然后进行计算。这样似乎有点麻烦，其实仔细观察不难发现这三个公司其实可以合并，第二种情况重叠面积为0，所以可以和第一种情况合并，第三种情况重叠面积就是小矩形，所以得出总覆盖面积=大矩形+小矩形-小矩形，还是可以和第一种情况合并，最终得出公式为总覆盖面积=矩形1+矩形2-重叠面积
接下来我们需要把核心放在求重叠面积上。对于第二种情况，我们可以先判断两个矩形是否重叠，这要如何判断呢？不重叠有以下四种情况
1.

2.

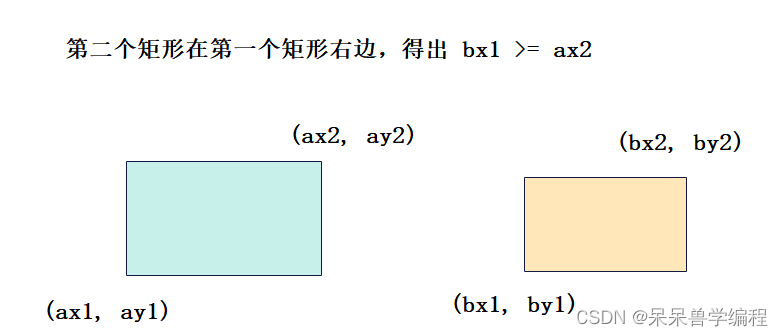
3.

4.

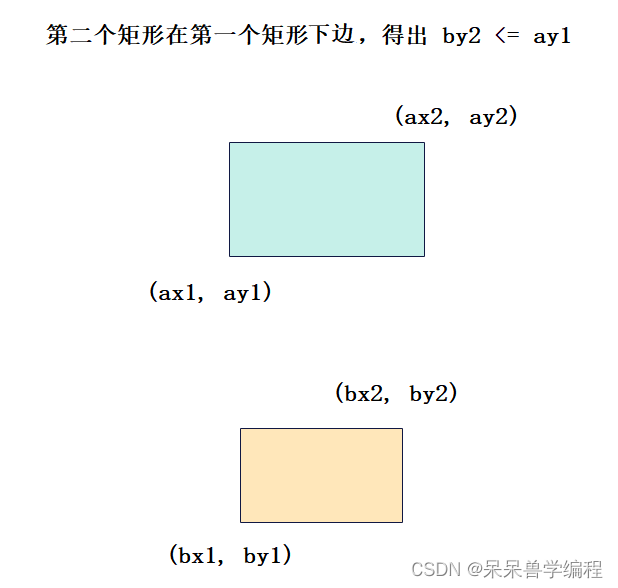
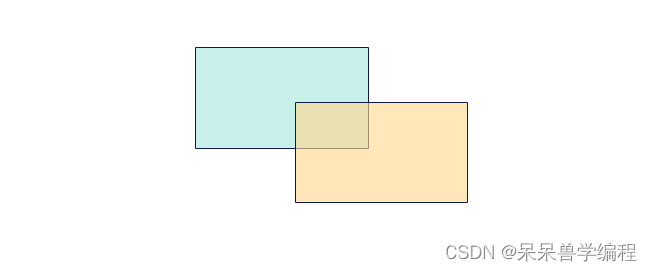
根据上面四个判断就能判断两个矩形是否重叠，如果不重叠，就需要计算重叠矩形面积了，先观察下图：

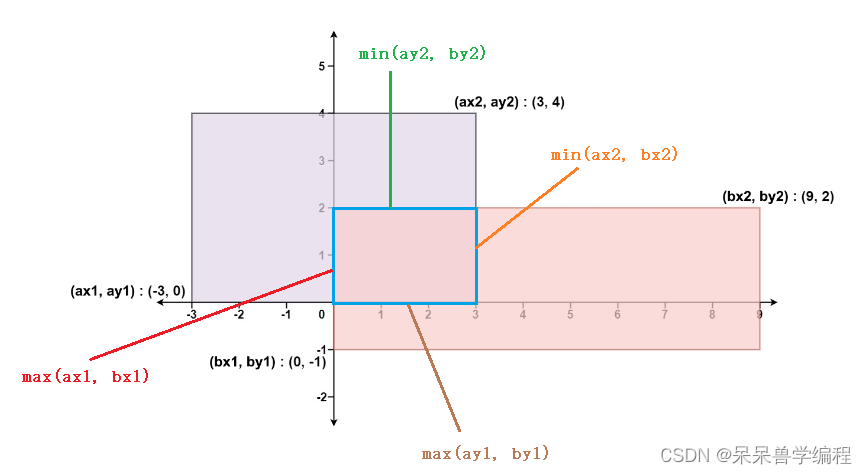
通过上图方式可以推导出重叠矩形的左下顶点和右上顶点，这要就可以计算出矩形面积（这个很简单，不用细说了）
根据上面一些推导再结合覆盖面积计算公式即可求出最终答案
代码实现：

class Solution {
public:
    int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int area1 = (ay2-ay1)*(ax2-ax1), area2 = (by2-by1)*(bx2-bx1);
        // 判断是否无重叠
        if (bx1 >= ax2 || bx2 <= ax1 || by1 >= ay2 || by2 <= ay1) {
            return area1 + area2;
        }
        int overlappingarea = (min(ax2, bx2)- max(ax1, bx1))*(min(ay2, by2)-max(ay1, by1));
        return area1-overlappingarea+area2;
    }
};