图片总结


内排序时间复杂度总结
- 内部排序:数据元素全部放在内存中的排序。
- . 在内排序当中比较快的有希尔排序,堆排序,快速排序,归并排序,这四个排序的时间复杂度都是O(n*logn)。其中希尔排序的时间复杂度更加准确的来说是O(n的1.3次方),对于希尔排序来说,它的时间复杂度计算非常之困难,所以直接记结论;对于堆排序来说,他的时间复杂度计算是通过错位相减法而算出来的;对于归并排序来说,它的时间复杂度倒是比快速排序稳定多了,还真就是雷打不动的O(logN)
- 然后直接插入排序,选择排序,冒泡排序时间复杂度都是O(N^2)
- 在四个比较快的排序当中,快速排序总体来说是最优的,虽然快速排序的时间复杂度受到单趟排序之后key最终落在的位置是否偏向于中间,乃至于快速排序在极端情况之下可以慢到O(N^2),但是好在有抢救方法,比如说三数取中。在最终测试完之后快速排序还是占优。
- 在这三个比较慢的排序当中,之前也有提到过,对于直接插入排序而言,不存在最好与最坏情况,都是雷打不动的O(N^ 2)。
- 对于冒泡排序而言,它最好的情况是O(N),对于直接插入排序而言,它最好的情况也是O(N)。那么这两个又怎么区分伯仲呢?总体而言是直接插入排序比冒泡排序更好,首先,如果这个待排序的数组是顺序有序的话,那么此时两者匹敌一样;如果说是接近有序的话,对于直接插入排序而言,也只需要在个别插入的过程后进行稍微微调一下;但对于冒泡排序的话,假设在某趟过后,整个数组已经是有序的情况之下,他又需要再去遍历一趟去确定已是有序,因此比直接插入排序要慢一点;两者最大的差距体现在部分有序的情况之下,与直接插入排序而言,当一个新元素需要融入到已经有序的数组当中的时候,在某些情况之下可以直接尾部插入而不用融入过程,可以省掉大量的步骤,对于冒泡排序而言,他对于部分有序并不敏感,因为他每一趟跑一次,只确定下来一个数放到最末尾,尽管你是部分有序,基本上还是接近了O(N^2)
外排序(文件排序)
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
- 对于外部排序而言,唯一的解药就是归并思想,用归并排序,与此同时,不要用递归版本,不然的话你懂的,把子文件数据在无限细分下去不是要分死了吗?因此需要用非递归的归并排序。具体的细节看我之前写的博客文件排序。
- 再回顾一下大概的过程:你说我现在在磁盘里面有1000个的数据,假设我内存里面最多能放得下100个数据。那我首先先从磁盘里面读100个数据到内存里面,然后在内存里面用快速排序,先把这100个数据给他排好,把这个读出来的,并且排好了的100个数据再放回新文件当中,然后再从磁盘里面剩下的900个数据当中再去读100个到内存里面来,然后再在内存里面用快速排序给他排好,然后再给他放到一个文件当中,然后现在已经有两个文件里面都是有序的数字,这时候用文件与文件的归并(跟内存已经没有关系了,内存里面是放不下的),然后继续不断向后再去读,再去归并…
排序的空间复杂度总结
- 对于直接插入排序,希尔排序,选择排序,冒泡排序,他们都是在原先的数组上进行直接改动,因此他们的空间复杂度都是O(1),不需要额外去创建一个新的辅助空间。
- 对于快速排序而言,我们知道由于它是一个递归,递归的话是必须要在原先函数的函数栈帧的低地址的地方再去不断的创建函数栈帧,再去不断的创建函数栈帧。递归有它的一个深度,这也是说为什么当递归层次太深的时候会发生栈溢出。如果是理想化的状态的话,我们知道整个快速排序递归的深度是O(logN),然后不排除极端恶心情况,此时递归的深度能够到O(N),因此他的空间复杂度介于O(logN)-O(N)。注意在每一层快速排序递归而创建的函数栈帧当中,在函数栈帧里面的各种变量啊什么的,他们的空间占用都可以算成O(1),也就是说单单就一个函数栈帧里面,其实也没有啥,主要是他在递归,在不断地向下拓展函数栈帧,这就有空间复杂度的增加了
- 对于归并排序而言,他也是在进行递归_MergeSort,它的递归的深度的话是标标准准的logN,但是对于递归而言,在外层非递归函数MergeSort,事先开辟了一个n个空间的额外辅助空间,N肯定是比logN大,因此总的空间复杂度就是O(N)
排序稳定性总结
- 在排序当中的稳定性,它并不是指这个性能稳不稳定。
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
- 比如说来打个简单的比方,在一个数组当中有两个5,在原先的乱序数组当中,可能两个5是隔开的,但也有一前一后之分。但是当排完序之后这两个5肯定是挨在一起了的,如果说这两个5的相对位置仍然保持不变,那么就叫这个排序是稳定的,否则就是不稳定。稳定性就是指相同数据的相对位置在排序之后是否会发生改变;如果不能保证相对位置不变,那么就是不稳定,否则就是稳定的。
- 直接插入排序是稳定的,因为直接插入排序相当于是一个新的数tmp不断的从右边想要融入到已经有序的这么一个数组当中,然后在融入的过程当中,如果说右边的数tmp小于已经有序数组的end所指向的数,那么这时候需要把end所指向的数向后移动一位,然后如果与end指向的数相等的话就直接融入进来,因此两个相等的数也根本就没有任何机会去进行前后交换
- 希尔排序是不稳定的,你去想想在一开始的预排序当中,两个相同的数据可能会被分到不同的组,然后进行预排序,然后一开始这个gap又那么大,很容易某个数据就飘到后面去了,控制不住了
- 选择排序也是不稳定的,给你举个反例就可以:

- 堆排序也超级不稳定,给你画个图,举个反例:
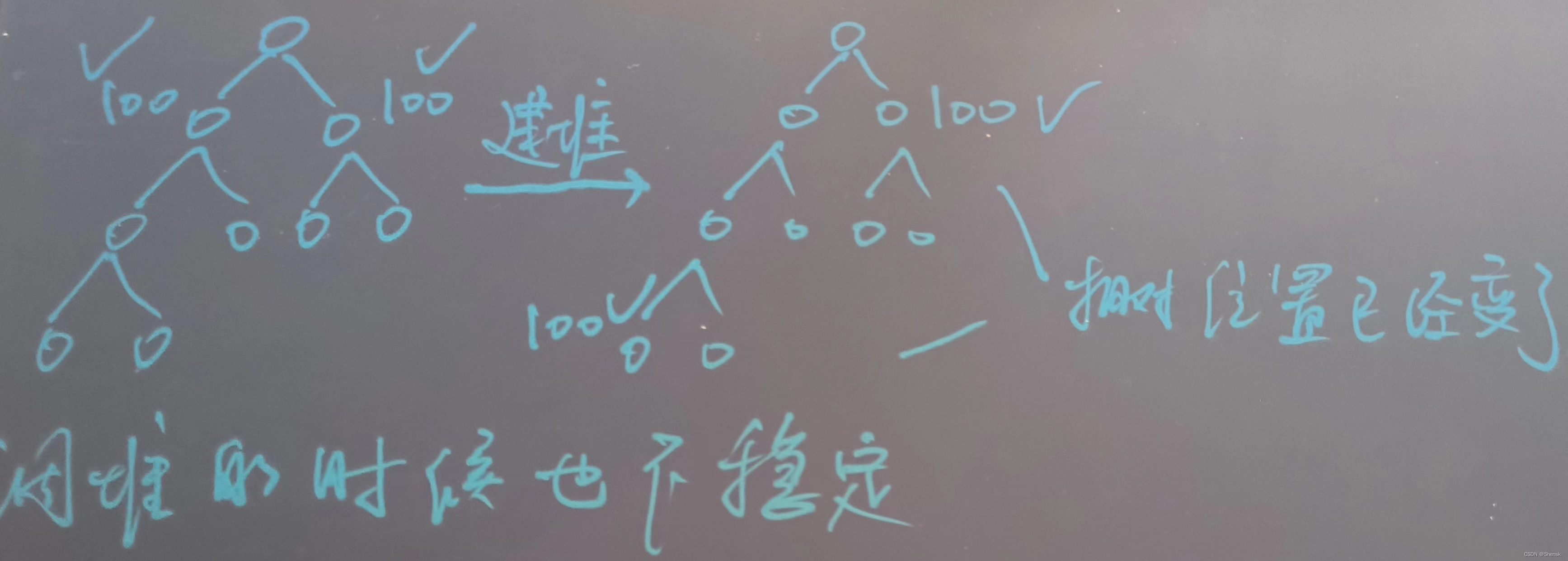
- 冒泡排序肯定是稳定的,冒泡排序就是一趟一趟一趟的去走,然后对于每一趟是两个相邻的数,两个相邻的数这么比下去,如果说我需要升序排列的话,当两个相邻的数当中,左边的数大于右边的数的话,两个数就要发生交换,然后如果说对于数组当中两个具有相同的值的数的话,根本就没有任何机会去进行前后交换,所以说是稳定的
- 快速排序也不稳定,给你画个图举个反例:
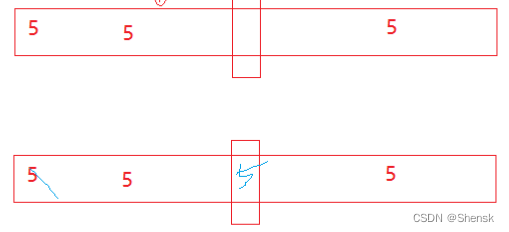
- 归并排序是稳定的,当然要把那个等号加上
while(begin1<=end1 && begin2<=end2)
{ //这边这个等号是关键
if (arr[begin1]<=arr[begin2])
{
tmp[k++]=arr[begin1++];
}
.........
}