一、说明
点的定位属于几何查找,是计算几何中的一个重要的问题。其包括点在三角形内外,多边形内外判断,平面剖分中的位置等。
二、点和几何区域的关系
2.1 点和线的位置关系
- 两个平行向量的叉乘等于0。
- 如果两个向量的叉乘等于0,且有一个公共点,那么它们共线。
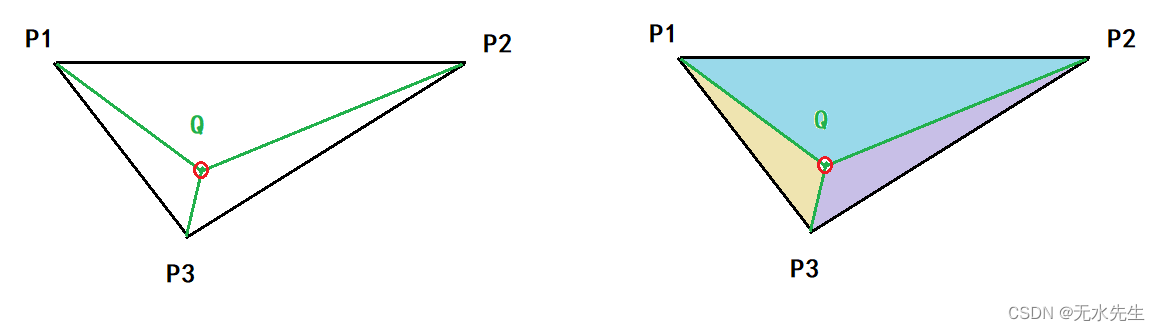
设点Q在线段 (P1,P2) 上。则:
1. (Q-P1)×(P2-P1)=0 ;( 保证Q 在线段 (P1,P2) 上)
此叉乘也是三角形的面积。
如图所示:

Q在线段P1P2上,🔺P1QP2 的面积为0;当Q1在P1P2线段外后,三角形🔺P1Q1P2的面积非零。
Code:
class Point:
def __init__(self,cx,cy):
self.x = cx
self.y = cy
def OnLine( P1, P2, Q):
diff = abs( (Q.x-P1.x)*(P2.y-P1.y)-(P2.x-P1.x)*(Q.y-P1.y) )
if(diff <0.0001 ):
return 1
return 0
p1 = Point(2,5)
p2 = Point(7,8)
Q = Point(4,6.2)
print( OnLine( p1,p2,Q ))
2.2 点和三角形的位置关系
点在平面内与三角形三个顶点中任意两点构成三个三角形。可以通过计算这三个三角形的面积和与原三角形面积来比较判断点是否在三角形内。
如果Q在三角形P1-P2-P2内,那么面积:
S(🔺P1-P2-P3) = S(🔺P1-P2-Q )+ S(🔺P1-Q-P3) +S( 🔺Q-P2-P3)
因此:
diff = | S(🔺P1-P2-P3)- S(🔺P1-P2-Q )+ S(🔺P1-Q-P3) +S( 🔺Q-P2-P3)|<0.001
就表明Q在三角形P1-P2-P2内
class Trial:
def __init__(self,c1,c2,c3):
self.p1 = c1
self.p2 = c2
self.p3 = c3
def TriArea(self):
diff = abs((self.p3.x - self.p1.x) * (self.p2.y - self.p1.y) - (self.p3.y - self.p1.y) * (self.p2.x- self.p1.x) )
return diff
def IsInTri(self,Q):
S = self.TriArea()
S1 = abs(( Q.x - self.p1.x) * (self.p2.y - self.p1.y) - (Q.y - self.p1.y) * (self.p2.x- self.p1.x) )
S2 = abs(( Q.x - self.p1.x) * (self.p3.y - self.p1.y) - (Q.y - self.p1.y) * (self.p3.x- self.p1.x) )
S3 = abs(( Q.x - self.p2.x) * (self.p3.y - self.p2.y) - (Q.y - self.p2.y) * (self.p3.x- self.p2.x) )
diff = abs( S - S1 -S2 -S3 )
if (diff<0.001):
return 1
return 0
p1 = Point(2,5)
p2 = Point(7,8)
p3 = Point(3,3)
tr = Trial(p1,p2,p3)
Q = [ Point(7,9 ),Point(7,8 ),Point(6,7),Point(3,1),Point(3,4) ]
Pd = [ tr.IsInTri(i) for i in Q ]
print( Pd)
结果:
[0, 1, 1, 0, 1]
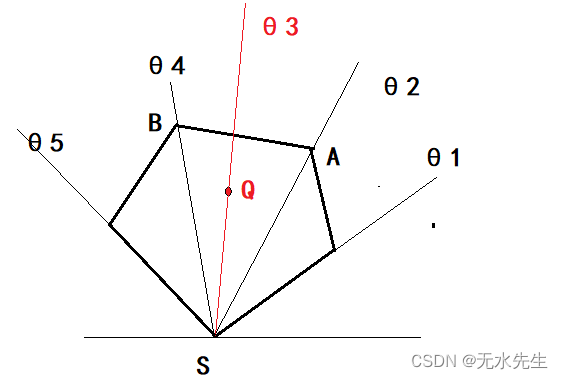
2.3 点和多边形的位置关系
对于多边形可以这样处理,
1)首先,找到一个顶点S,(比如最下坐标的点)。
2)从S到所有顶点作向量。
3)将向量们的方向角按逆时针排序。
4)找Q方向的相邻顶点AB。
5) 如果判别Q是否在三角形SAB的内部。(在内部,Q就一定在多边形内部)