第一章 数据结构(温习数据结构的内容)
1.1 树基本结构介绍
树具有的特点:
每一个节点有零个或者多个子节点
没有父节点的节点称之为根节点,一个树最多有一个根节点。
每一个非根节点有且只有一个父节点
| 名词 | 含义 |
|---|---|
| 节点 | 指树中的一个元素 |
| 节点的度 | 节点拥有的子树的个数,二叉树的度不大于2 |
| 叶子节点 | 度为0的节点,也称之为终端结点 |
| 高度 | 叶子结点的高度为1,叶子结点的父节点高度为2,以此类推,根节点的高度最高 |
| 层 | 根节点在第一层,以此类推 |
| 父节点 | 若一个节点含有子节点,则这个节点称之为其子节点的父节点 |
| 子节点 | 子节点是父节点的下一层节点 |
| 兄弟节点 | 拥有共同父节点的节点互称为兄弟节点 |
1.2 二叉树
如果树中的每个节点的子节点的个数不超过2,那么该树就是一个二叉树。
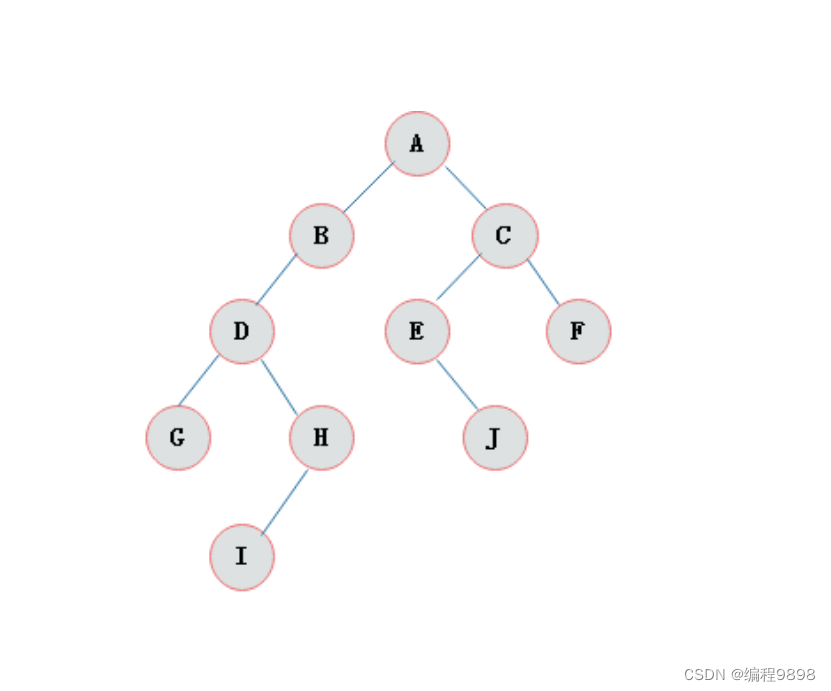
1.3二叉查找树/二叉排序树
二叉查找树的特点:
-
左子树上所有的节点的值均小于等于他的根节点的值
-
右子树上所有的节点值均大于或者等于他的根节点的值
-
每一个子节点最多有两个子树
案例演示(20,18,23,22,17,24,19)数据的存储过程;
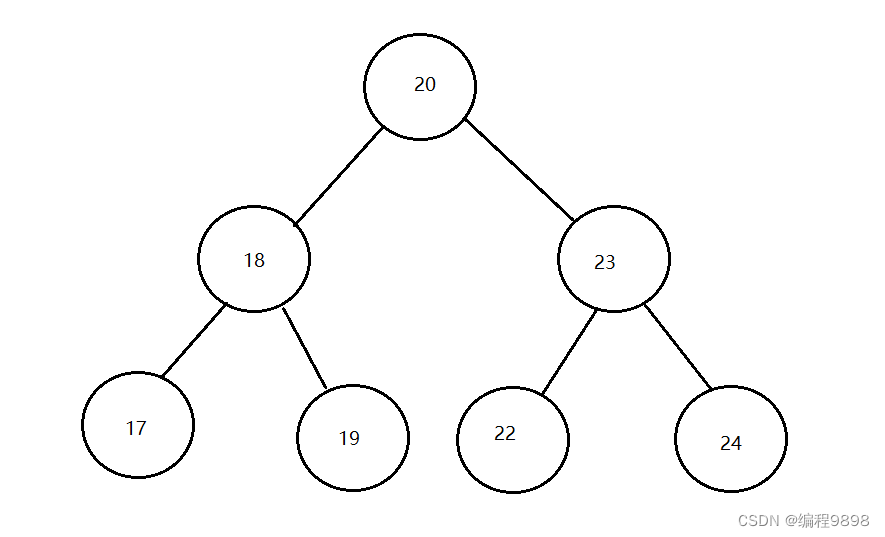
增删改查的性能都很高!!!
遍历获取元素的时候可以按照"左中右"的顺序进行遍历;
注意:二叉查找树存在的问题:会出现"瘸子"的现象,影响查询效率。
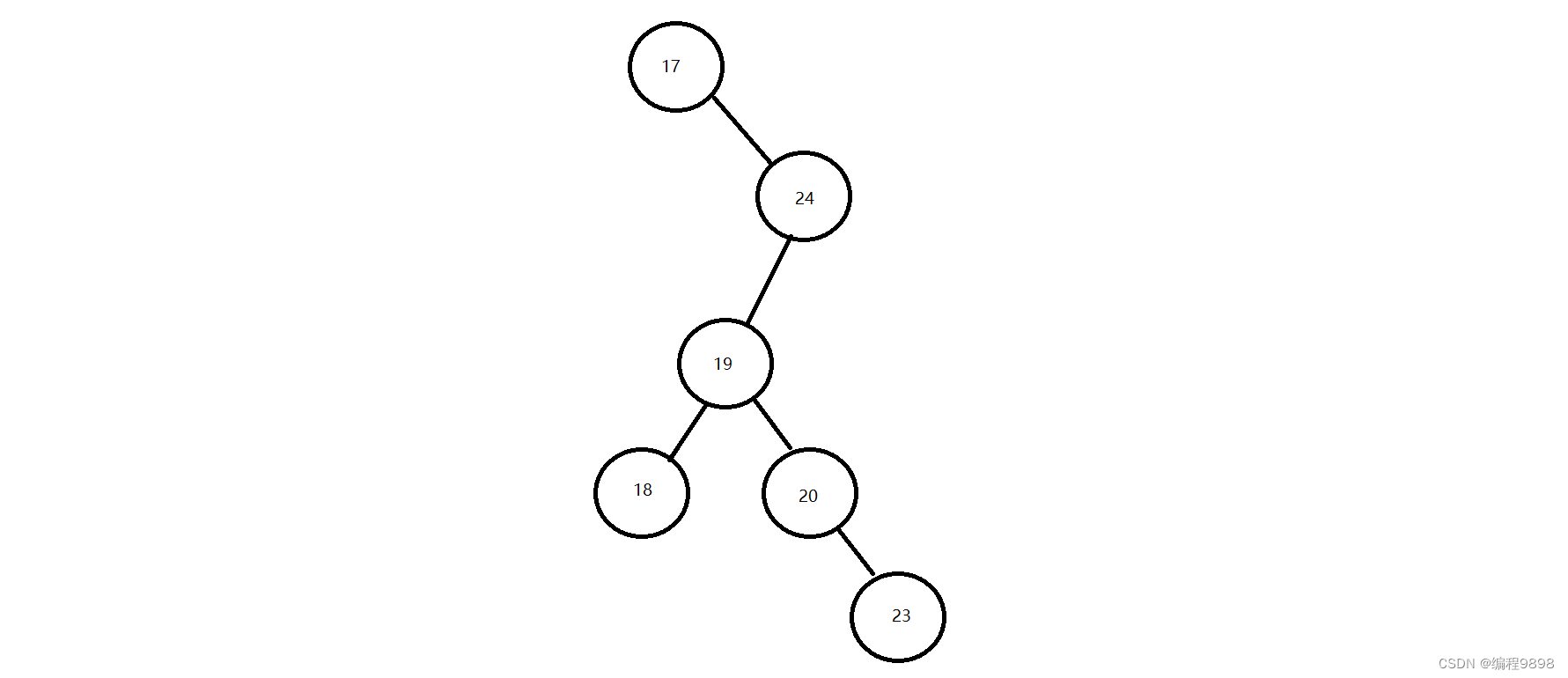
1.4平衡二叉树
(基于查找二叉树,但是让树不要太高,尽量元素均衡)
概述
为了避免出现"瘸子"的现象,减少树的高度,提高我们的搜素效率,又存在一种树的结构:"平衡二叉树"
规则:它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
如下图所示:
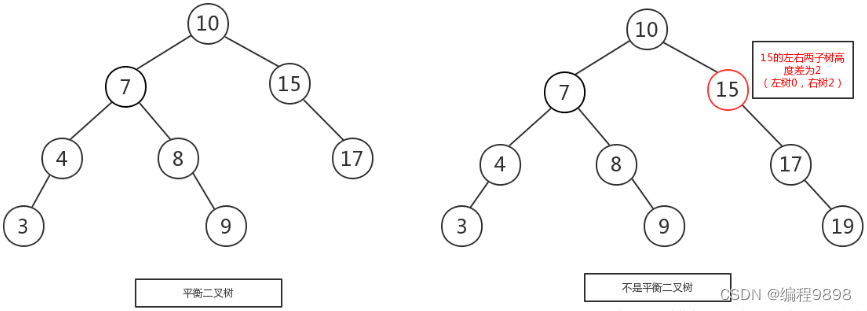
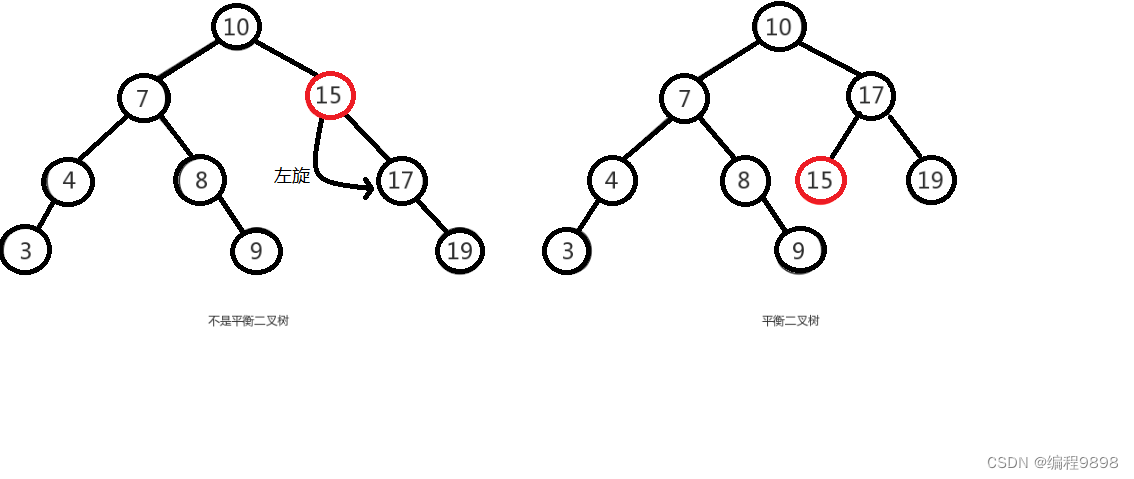
如下图所示,左图是一棵平衡二叉树,根节点10,左右两子树的高度差是1,而右图,虽然根节点左右两子树高度差是0,但是右子树15的左右子树高度差为2,不符合定义,
所以右图不是一棵平衡二叉树。
旋转
在构建一棵平衡二叉树的过程中,当有新的节点要插入时,检查是否因插入后而破坏了树的平衡,如果是,则需要做旋转去改变树的结构。
左旋:
左旋就是将节点的右支往左拉,右子节点变成父节点,并把晋升之后多余的左子节点出让给降级节点的右子节点;
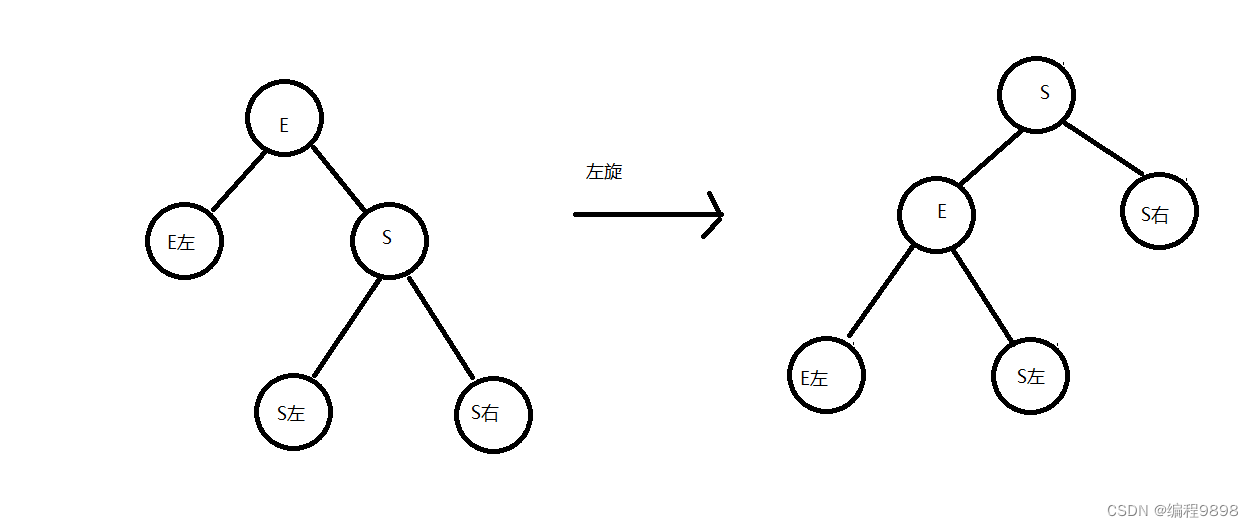
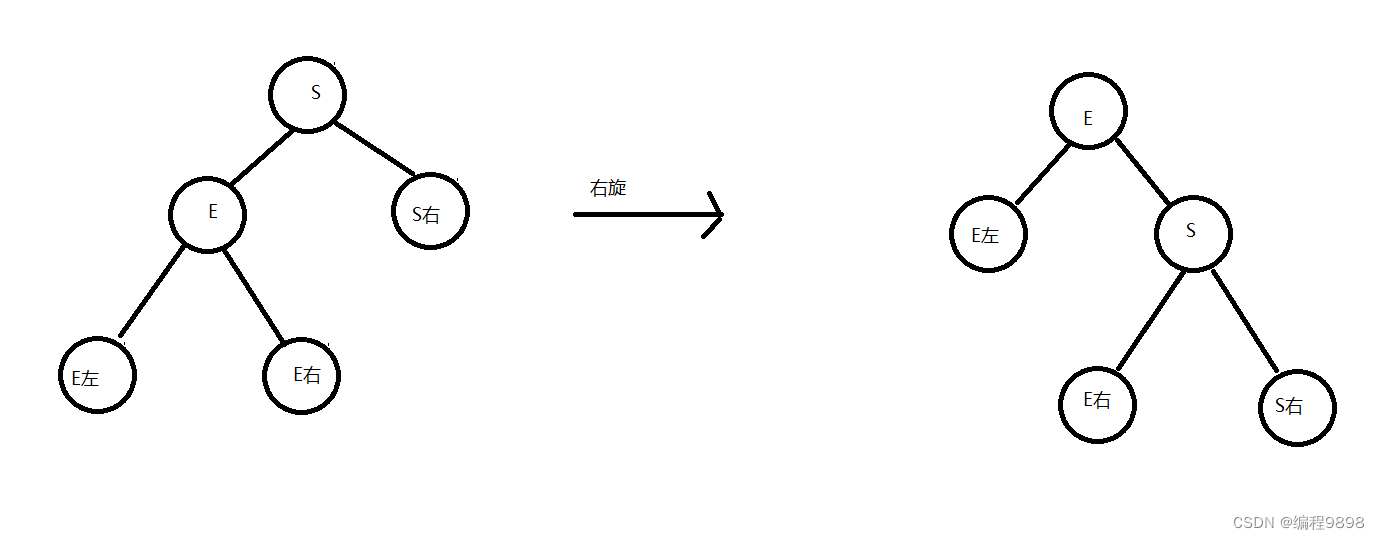
右旋:
将节点的左支往右拉,左子节点变成了父节点,并把晋升之后多余的右子节点出让给降级节点的左子节点
举个例子,像上图是否平衡二叉树的图里面,左图在没插入前"19"节点前,该树还是平衡二叉树,但是在插入"19"后,导致了"15"的左右子树失去了"平衡",
所以此时可以将"15"节点进行左旋,让"15"自身把节点出让给"17"作为"17"的左树,使得"17"节点左右子树平衡,而"15"节点没有子树,左右也平衡了。如下图,
由于在构建平衡二叉树的时候,当有新节点插入时,都会判断插入后时候平衡,这说明了插入新节点前,都是平衡的,也即高度差绝对值不会超过1。当新节点插入后,
有可能会有导致树不平衡,这时候就需要进行调整,而可能出现的情况就有4种,分别称作左左,左右,右左,右右。
左左
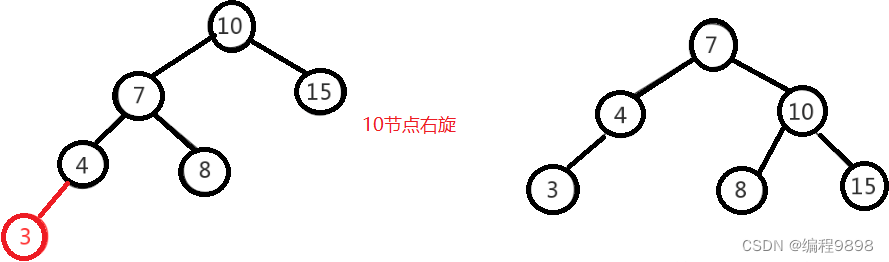
左左即为在原来平衡的二叉树上,在节点的左子树的左子树下,有新节点插入,导致节点的左右子树的高度差为2,如下即为"10"节点的左子树"7",的左子树"4",插入了节点"5"或"3"导致失衡。
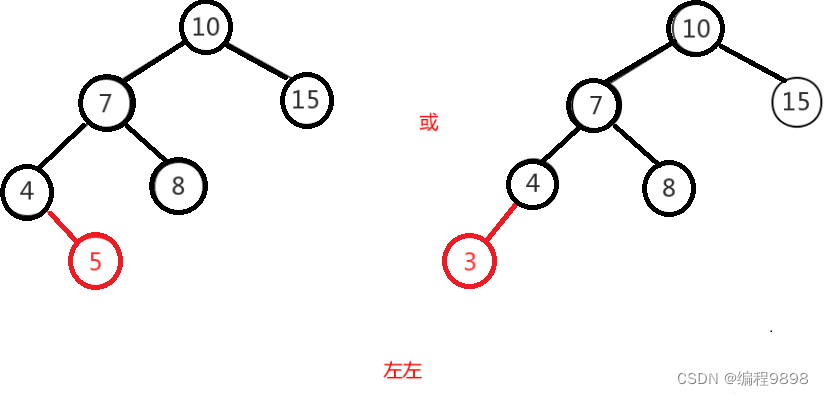
左左调整其实比较简单,只需要对节点进行右旋即可,如下图,对节点"10"进行右旋,
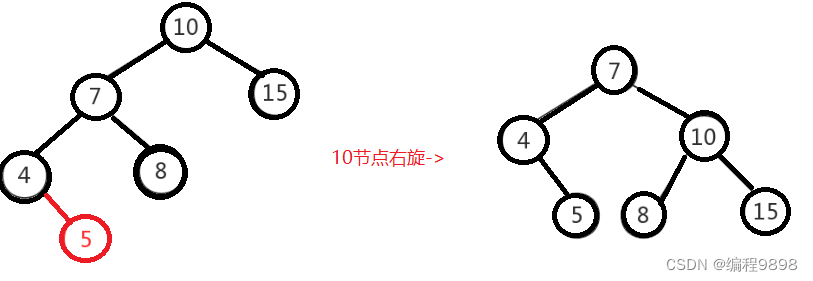
再旋转:
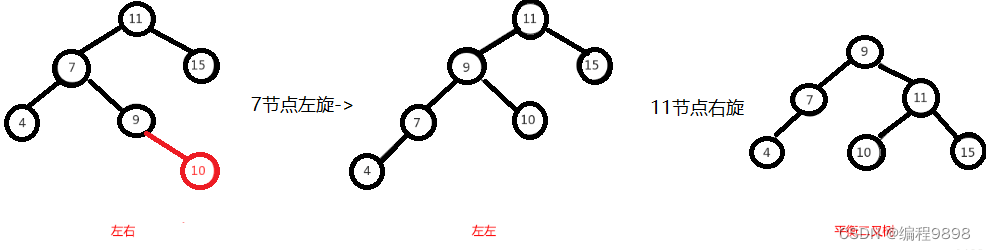
左右
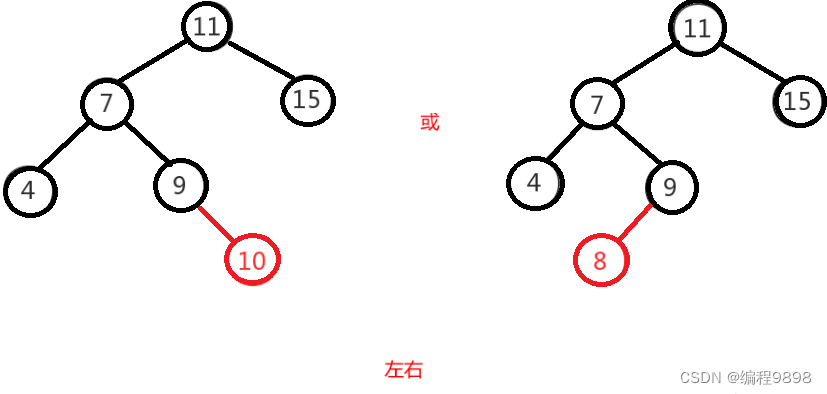
左右即为在原来平衡的二叉树上,在节点的左子树的右子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为"11"节点的左子树"7",的右子树"9",
插入了节点"10"或"8"导致失衡。
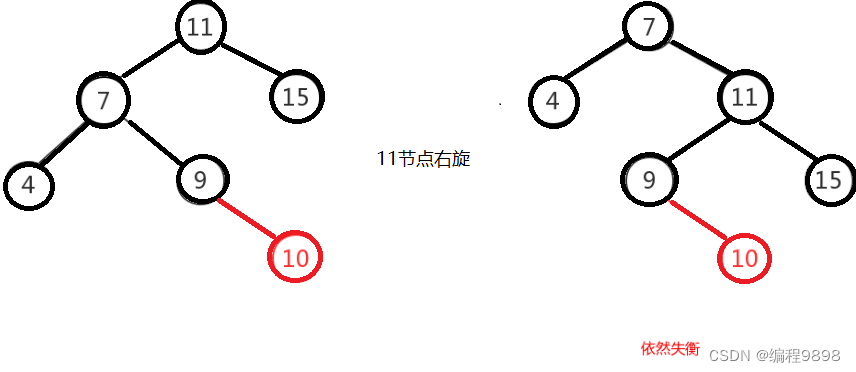
左右的调整就不能像左左一样,进行一次旋转就完成调整。我们不妨先试着让左右像左左一样对"11"节点进行右旋,结果图如下,右图的二叉树依然不平衡,而右图就是接下来要
讲的右左,即左右跟右左互为镜像,左左跟右右也互为镜像。
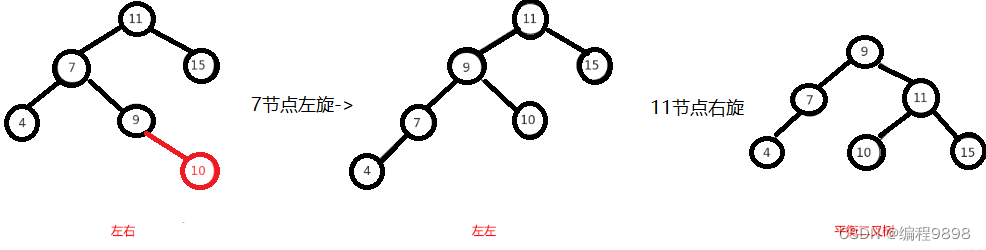
左右这种情况,进行一次旋转是不能满足我们的条件的,正确的调整方式是,将左右进行第一次旋转,将左右先调整成左左,然后再对左左进行调整,从而使得二叉树平衡。
即先对上图的节点"7"进行左旋,使得二叉树变成了左左,之后再对"11"节点进行右旋,此时二叉树就调整完成,如下图:
右左
右左即为在原来平衡的二叉树上,在节点的右子树的左子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为"11"节点的右子树"15",的左子树"13",
插入了节点"12"或"14"导致失衡。
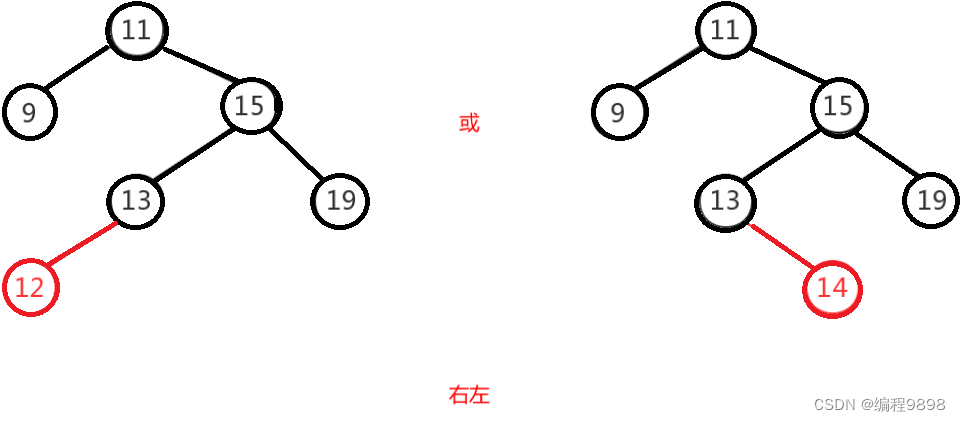
前面也说了,右左跟左右其实互为镜像,所以调整过程就反过来,先对节点"15"进行右旋,使得二叉树变成右右,之后再对"11"节点进行左旋,此时二叉树就调整完成,如下图:
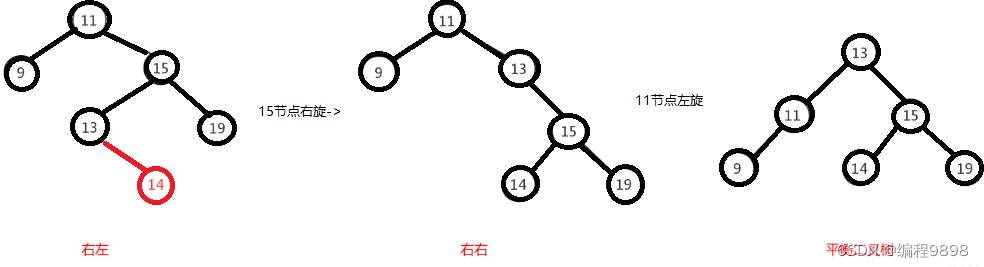
右右
右右即为在原来平衡的二叉树上,在节点的右子树的右子树下,有新节点插入,导致节点的左右子树的高度差为2,如下即为"11"节点的右子树"13",的左子树"15",插入了节点
"14"或"19"导致失衡。
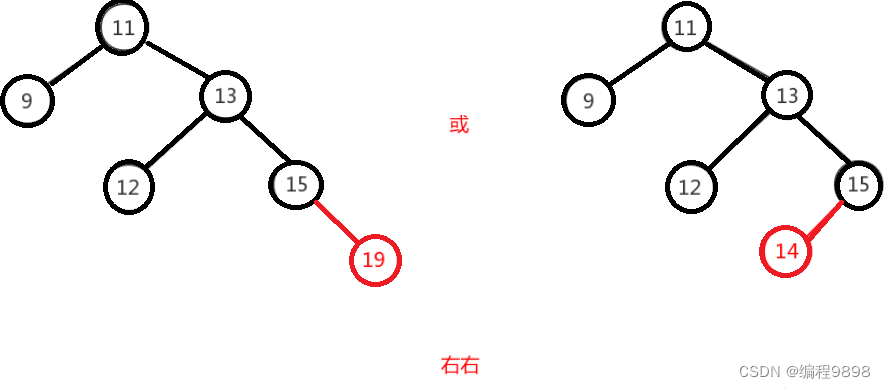
右右只需对节点进行一次左旋即可调整平衡,如下图,对"11"节点进行左旋。
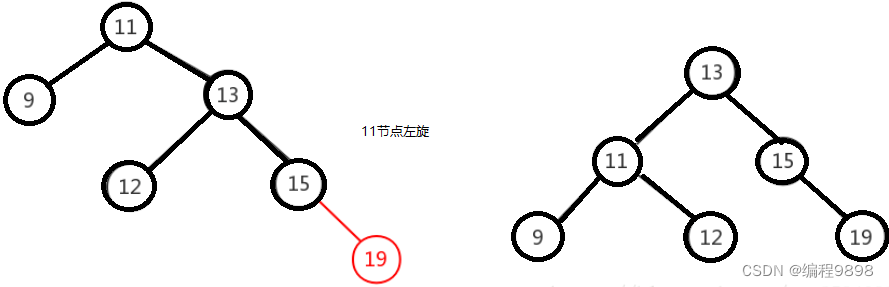
1.5红黑树
概述
红黑树是一种自平衡的二叉查找树,是计算机科学中用到的一种数据结构,它是在1972年由Rudolf Bayer发明的,当时被称之为平衡二叉B树,后来,在1978年被
Leoj.Guibas和Robert Sedgewick修改为如今的"红黑树"。它是一种特殊的二叉查找树,红黑树的每一个节点上都有存储位表示节点的颜色,可以是红或者黑;
红黑树不是高度平衡的,它的平衡是通过"红黑树的特性"进行实现的;
红黑树的特性:
每一个节点或是红色的,或者是黑色的。
根节点必须是黑色
每个叶节点(Nil)是黑色的;(如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点)
如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)
对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点;
总结就是:左根右,根叶黑,不红红,黑路同
如下图所示就是一个
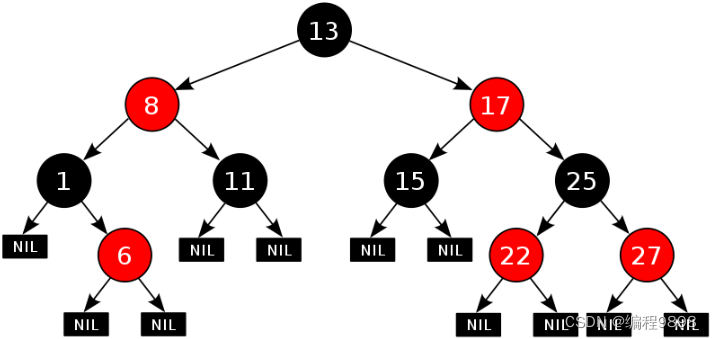
在进行元素插入的时候,和之前一样; 每一次插入完毕以后,使用黑色规则进行校验,如果不满足红黑规则,就需要通过变色,左旋和右旋来调整树,使其满足红黑规则;