曾陪经理一起面试，问过一个问题：

CUBIC 的公式：
$W(x)=C(x-K{)}^3+W_{max}$

其中 x 是什么意思？

本意是想候选人回答 “x 是绝对时间”，然后我会接着问 “这个 x 如何采样？”

候选人巧妙绕开了问题，说了句无关紧要的话，解释了一下传输优化的概念…

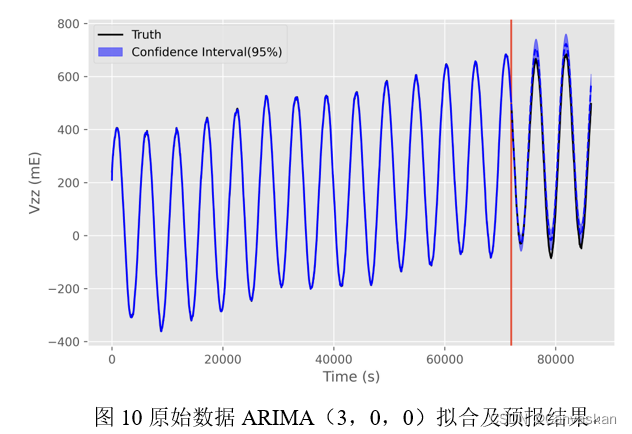
昨天与同事讨论问题，又想起这个，来解释一下。参见下图，这是 CUBIC 在一个 AIMD 周期的 cwnd/time 图：

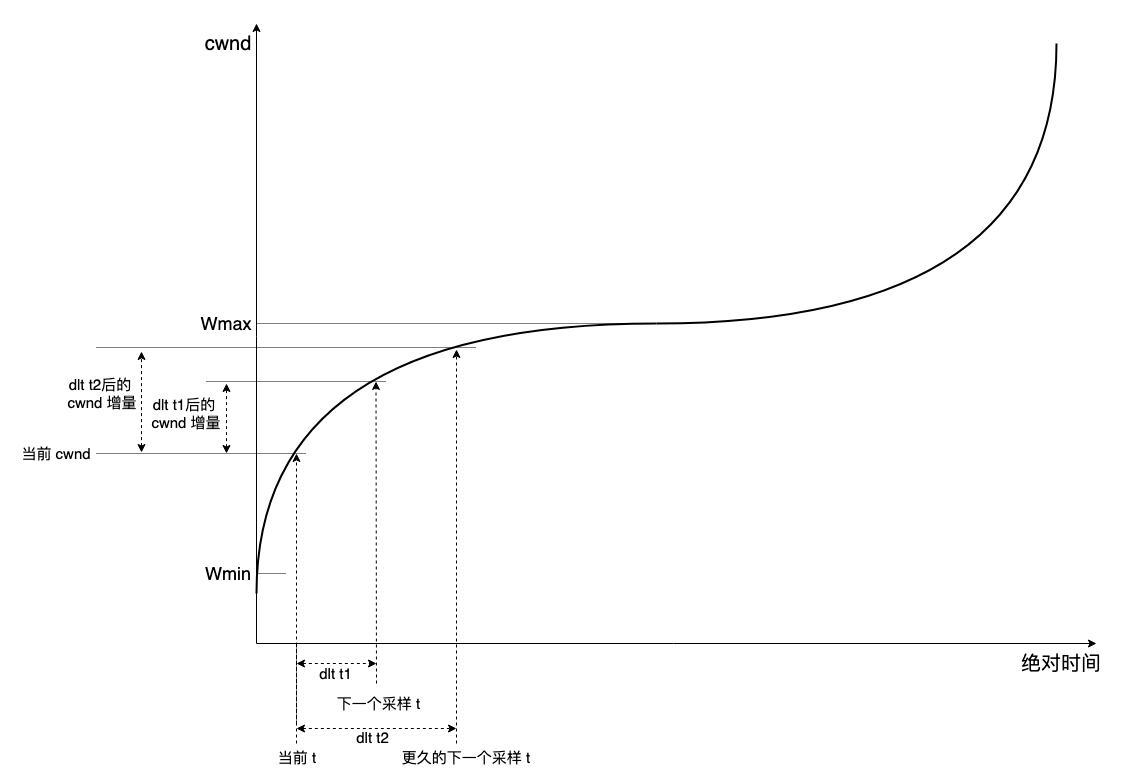
横轴表示 “绝对时间”，因此 CUBIC 的特点之一是 “RTT 无关”，只要给定一个距离 AIMD 周期开始的 delta time，就能算出相对于周期开始时 Wmin 的增量。

第一个问题，x 即 “距离当前周期开始的绝对时间”。现在看第二个问题，x 如何采样。

TCP 由 ACK 时钟驱动，每收到一个 ACK，均要计算 cwnd 作为发送配额，针对第二个问题简单的回答就是 “ACK 到达时采样计算”，此样本将用来计算 “直到下一次采样点为止 cwnd 的增量”，目的是保证在下一次采样点(一般意义上即下一个 ACK 到达)之前，有充足的 cwnd 配额可供持续发送数据。

更深一步的问题就来了，delta time 的值如何取呢？这是一个预测未来的问题，即 “下一个 ACK 最短以及最长何时到达？”

为回答该问题，先看另一个问题，delta time 太长或太短分别会怎样？

ACK 到达，采样打点就是为了绘制这条曲线，采样打点越密集，曲线越光滑，反之则会变成马赛克楼梯状。结论很明确：考虑到 ACK 持续到达，delta time 越小，cwnd 增量越小，发送越平滑，delta time 越大，cwnd 增量越大，发送行为越突发。

拥塞大多与突发有关，好的拥塞控制要旨即控制突发，最佳策略就是 “delta 设置为 ACK 持续到达的间隔”，例如，如果 ACK 以 5us(or 更小) 为间隔到达，则 delta time = 5us，下一个 5us 的 cwnd 增量即这段时间的发送配额，这是个极短时间段内的极小增量，保持和 ACK 时钟 pacing 一致，本质上就是 pacing，避免了突发。

不光如此，cwnd 增量过大还可能导致乐观预测未来，预支过多带宽而丢包，最好的方法还是一步一个小脚印。无论从突发角度还是从乐观预支角度，都倾向于使用一个极小的 delta time。

但现实没有这么理想，TCP 自带两种突发：

• 每次发送一个 mss 大小的段而不是 1 字节；
• ACK 会 delay 至一个 RTT 而积累，ACK 也可能被聚合突发到达。

因此 delta time 不能任意小，否则当这么短的时间段过去后，下一个 ACK 尚未到达，造成 cwnd 配额用尽而进入空窗期无法再继续发送。反过来，delta time 肯定也不能太大。

Linux TCP 选择的是 minrtt，可能真有点小，但这么久的时间收不到一个 ACK 也属罕见。

如果想使用极小的 delta time 绘制极光滑的 CUBIC 曲线就要抛弃 ACK 时钟，自己设置定时器(如 Linux hrtimer)驱动曲线的绘制，比如每 1us or 5us 滴答一下，计算 cwnd 增量作为接下来的时钟周期内的发送配额。

关于文初的问题，就说到这里，按我的惯例，下面就着这个问题继续引申。

CUBIC 除了 RTT 无关外，还有第二个特征，即 cwnd 谨慎逼近 Wmax 后快速 probe。这两个特征都来自对 BIC 的反复。

CUBIC 第二个特征继承自 BIC 的二分搜索，但 BIC 与 RTT 相关，利好短 RTT，CUBIC 解决了这问题，RTT 无关也就成了 CUBIC 的特征。这就是 CUBIC 与 BIC 的渊源，至于 BIC，它本就是对 TCP Reno AIMD 行为的优化。

问题来了，CUBIC 只是实现第二个特征的一种方式，而非唯一方式，我看 CUBIC 实现时，甚纠结，Linux kernel 描绘三次曲线非常费劲，于是我想到另一个方法：双斜率直线，叫 TCP DoubleLine：

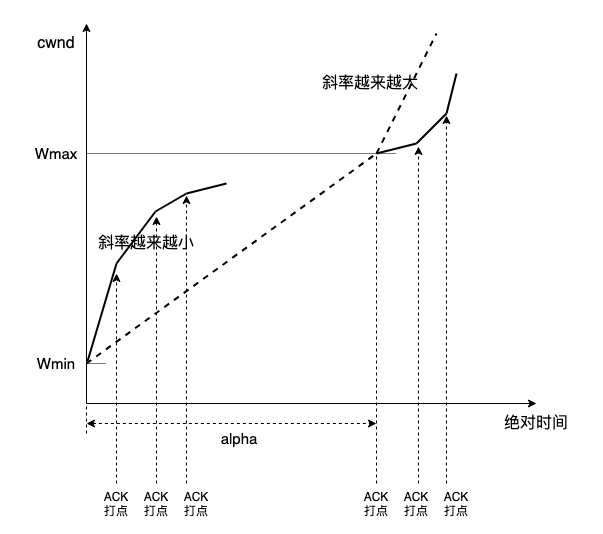
学 CUBIC 的样子，“找出” 一族曲线并不难，和 CUBIC 三次曲线一样，剩下的交给调参：

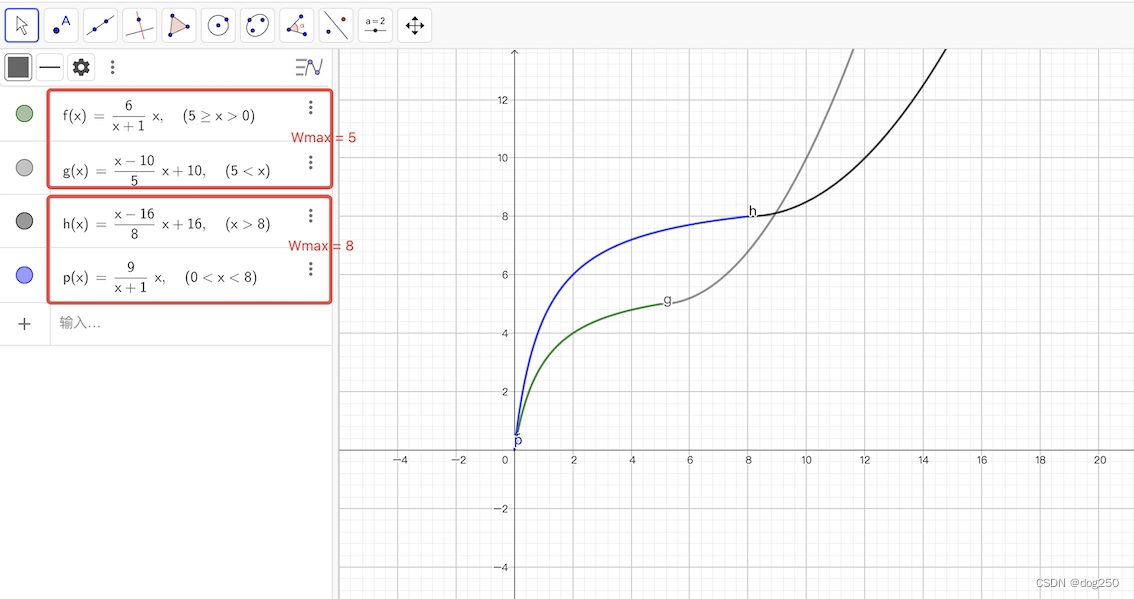
其本质含义和 CUBIC 没什么不同，RTT 无关，且 “谨慎逼近 Wmax 后加速 probe”，但显然线性计算或二次曲线比 CUBIC 计算变得更简单。

更普遍地，可以不操作斜率，直接部署两条真直线，可看作 Standard TCP 的 RTT 无关版：

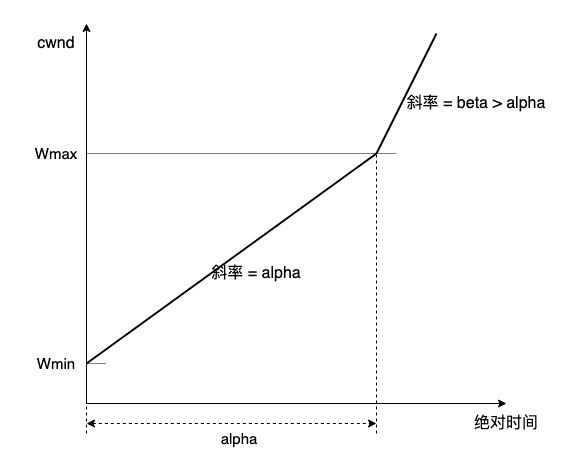
甚至可以再去掉一个约束，连双斜率也不要，仅保留一条直线：y = alpha * x，其中 0 < x < Wmax/alpha：
https://github.com/marywangran/tcp_line

这种可能更适合 Wi-Fi 等毫无规律的场景，无规律就不能有任何假设，谨慎逼近 Wmax 后加速 probe，只能适得其反，还是纯 AIMD 最简单，无益也无害。模仿骰子猜数字，永远随机猜胜率最高。

说起 TCP 端到端拥塞控制，CUBIC 已在顶端，信息有限的约束下，没任何算法能识别随机丢包和拥塞丢包，更别提精确识别了。很多人推崇 BBR，认为 BBR 高带宽在于抵抗随机丢包，但 BBR 要付出其它代价，简单说就是赌博。

BBR 依靠的只是 “观望一会儿再看一下” 这种硬扛的方法应对丢包(BBR2 采用了更锉的方案，引入一个丢包率，大于这个比率才反应)，如果真是随机丢包就赌赢了，万一是真拥塞就意味着输掉赌注，大丢包大重传。和 CUBIC 一样，BBR 也靠猜，不同的是，CUBIC 无差别响应丢包，而 BBR 靠信念赌博，对待丢包这件事上，BBR 往左，CUBIC 往右而已。

为什么 BBR 吞吐比 CUBIC 高？以上这段话可以解释。同时，正如 BBR 作者之一本人所说：

BBR is not trying to maintain a higher throughput than CUBIC in these kinds of scenarios with steady-state bulk flows. BBR is trying to be robust to the kinds of random packet loss that happen in the real world when there are flows dynamically entering/leaving a bottleneck.

在公平视角，BBR 并没有抢占更多 CUBIC 流的带宽，它只是恰好填充了由于 CUBIC 流对丢包对无差别反应而主动丢失的带宽，即便利用本来已经被 CUBIC 流 “浪费” 掉的带宽，纯想捡漏，BBR 也要以高重传率押注。
综合来看，虽然 CUBIC 吞吐不及 BBR，但相比 BBR，CUBIC 更加平衡，也就更加优秀：

CUBIC 作为使用最普遍的 cca 不是没有原因的，综合效能来看，CUBIC 已经到了非常高的位置，因此在很多系统中它都是缺省算法，无论从效率还是公平性来看都非常不错。但大家普遍推崇 BBR，因为在更多人眼里，所谓的 “意义” 就是吞吐高，而 BBR 恰好满足这一特征。但正如文末的图示所示，比这个更重要的是全局公平。

浙江温州皮鞋湿，下雨进水不会胖。