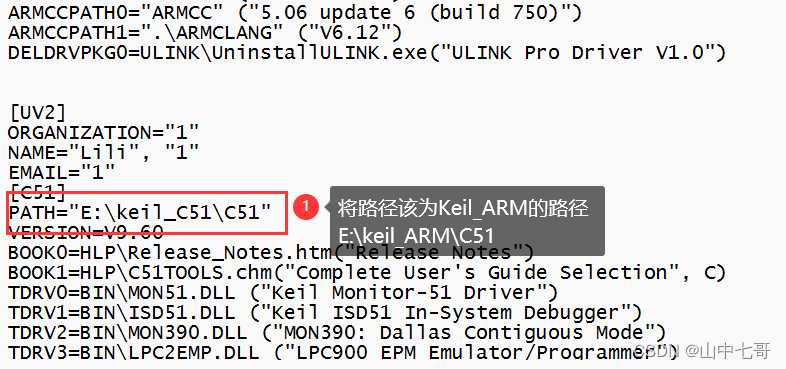
搜索路径状态记录

1076. 迷宫问题 - AcWing题库

//以最简单的迷宫问题为例，如何记录走迷宫的路径，其实只需要记录一下状态即可
//也就是记录一下这个点是从哪个点来的，最后从终点开始输出即可（此时输出的是逆序）
#include<iostream>
#include<cstdio>
#include<queue>

using namespace std;

typedef pair<int,int> PII;

const int N = 1010;
const int dx[]={0,0,1,-1}, dy[]={1,-1,0,0};

int n;
int maze[N][N];
PII path[N][N]; //记录每个点的来源

void bfs()
{
    queue<PII> q;
    q.push({0,0});
    
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        int x = t.first, y = t.second;
        
        for(int i = 0 ; i < 4; i ++)
        {
            int nx = x + dx[i], ny = y + dy[i];
            
            if(nx >= 0 && nx < n && ny >= 0 && ny < n && !maze[nx][ny])
            {
                maze[nx][ny] = 1;
                q.push({nx,ny});
                path[nx][ny] = t;
            }
        }
    }
}
/*****************************************************************/
void dfs(int x ,int y)  //递归的输出答案路径
{
    if(x == 0 && y == 0)
    {
        printf("0 0\n");
        return;
    }
    
    dfs(path[x][y].first, path[x][y].second);
    printf("%d %d\n", x, y);
}
/*****************************************************************/

int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i ++)
        for(int j = 0; j < n ; j ++)
            scanf("%d", &maze[i][j]);
    bfs();
    dfs(n-1, n-1);
    return 0;
}

多源BFS问题

173. 矩阵距离 - AcWing题库

//由于BFS的特效，我们处理多源的问题的时候，仅仅只需要把所有的起点（Flood-fiil的点）
//加入队列中即可，用这些点去更新其他点到这些点的距离，当某个点第一次被访问
//就说明是与它距离最近的点访问到了它，此时就是最短距离
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>

using namespace std;

typedef pair<int,int> PII;

const int N = 1010;

int n,m;
int dist[N][N];
char g[N][N];
queue<PII> q;

void bfs()
{
    int dx[]={0,1,0,-1}, dy[]={1,0,-1,0};
    
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        for(int i = 0; i < 4;  i ++)
        {
            int x = t.first + dx[i], y = t.second + dy[i];
            
            if(x < 0 || y < 0 || x >= n ||  y >= m) continue;
            if(dist[x][y] != -1) continue;
            
            dist[x][y] = dist[t.first][t.second] + 1;
            q.push({x,y});
        }
    }
}
int main()
{
    memset(dist, -1, sizeof dist);
    
    scanf("%d%d", &n, &m);
    
    for(int i = 0 ; i < n ; i ++)
    {
        scanf("%s", g[i]);
        for(int j = 0 ; j < m ; j++)
            if(g[i][j] == '1')
            {
                q.push({i,j});
                dist[i][j] = 0;
            }
    }
    bfs();
    for(int i = 0 ; i < n; i ++)
    {
        for(int j = 0 ; j < m ; j ++)
            printf("%d ", dist[i][j]);
        puts("");
    }
    return 0;
}

双向广搜优化

177. 噩梦 - AcWing题库

190. 字串变换 - AcWing题库

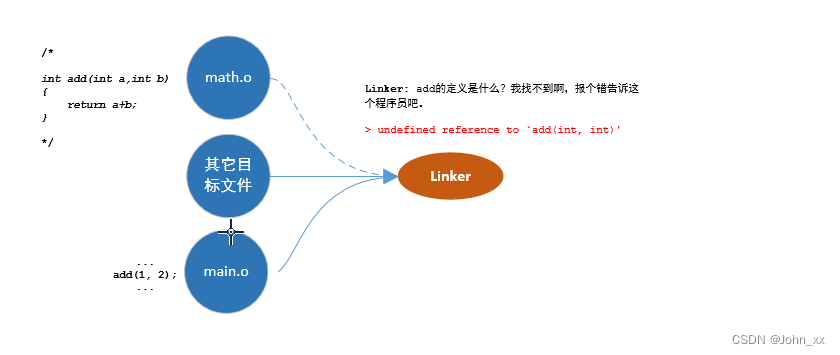
//双向广搜是一个优化效果很好的算法，往往我们从一个点开始搜索状态，其数量是很庞大的，下面用
//图像来表示该算法的优化效果
//双向广搜常用来优化类似于字串变换这种把一个图，一个字符串当作一个状态来表示的题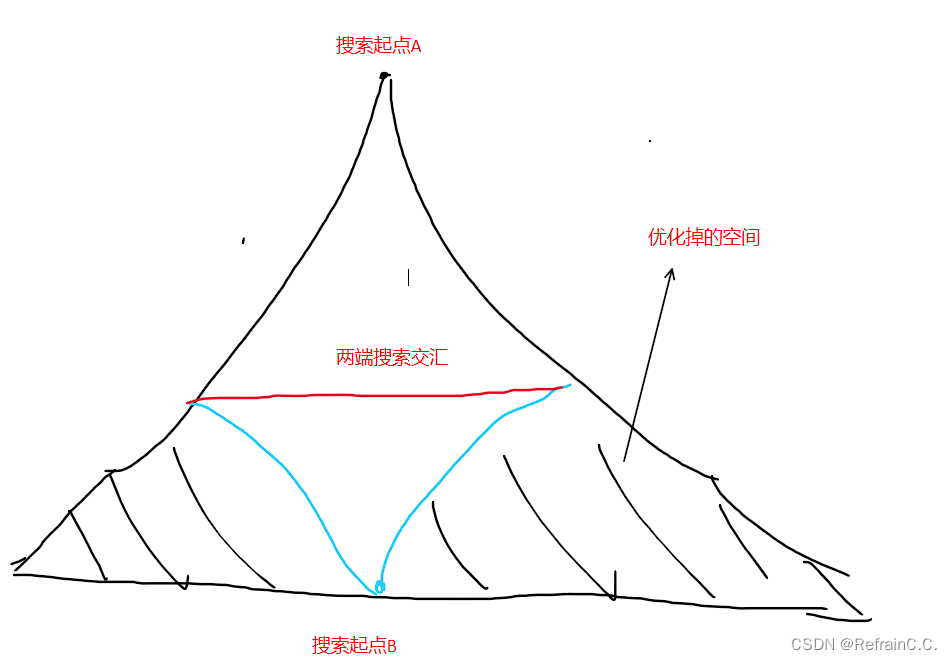

 

不同边权的BFS问题之01边权

175. 电路维修 - AcWing题库

3675. 逃离迷宫 - AcWing题库

//在处理不同边权的问题时，我们为了保证BFS队列中的单调性和两段性
//ps：不知道什么是单调性和两段性的可以去翻看算法竞赛进阶指南
//我们把通过代价较小的边到达的点加入到队头，把代价耗费较大的加入到队尾
//每个点可以多次入队，但是类似于dijkstra算法，每个点出队的时候就一定是最优解
//所以记录下每个点出队的状态即可

不同边权的BFS问题之优先队列优化 

176. 装满的油箱 - AcWing题库

//其实就是堆优化版的dijkstra
//当每条边的权重都不相同的时候，我们为了保证每次从队列中取出的元素是代价耗费最小的状态
//我们利用优先队列的性质，即按权重处理大小，每次取出队头元素就保证了权重最小的状态
//同样的，我们允许每个状态（点）多次入队，但是一旦出队就是最优解，记录一下即可

BFS优化之Astar算法 

179. 八数码 - AcWing题库

178. 第K短路 - AcWing题库

//为了提高搜索效率，我们在用“从起始状态到当前状态耗费代价大小”为依据去每次选择最小
//的状态出队更新的基础上，再额外增加一个出队的依据
//“当前状态到目标状态的估计耗费”
//这样我们以“总代价”=“从起点出发已经耗费的代价”+“预计到终点需要耗费的代价”为标准
//每次选择“总代价”最小的状态出队扩展
//故以此特性我们需要在普通BFS的基础上作出两点改进
//*1，改用优先队列，大小排序的标准为“总代价”
//*2，设计“估价函数”f(state)，用于估计出当前状态到目标状态所需耗费的代价

//对于第二点的f（state），我们要求估计值≤实际值
//实际题目中，f（state）的设计是很套路，模板化的，本身需要用到Astart的题就很少

 搜索状态记录之二进制存储 

166. 数独 - AcWing题库

//以经典例题数独为例，讲解用二进制存储状态的方法

//前置知识

//与，或，非，异或，左移，右移这几个二进制数位运算
//本题中，我们需要记录每一行每一列每一个子九宫格中可以用以及用了哪些数字

//用数字的二进制位去存储状态
//每行,每列,每个九宫格,一共9个状态,就只要一个9位的二进制数
//9个位置的数字,1表示可以用,0表示不能用
//那么对于每一个空位上可以用的数字，我们只需要将用于记录这一行这一列这一个九宫格的二进制数
//做一遍&运算，即可求得交集，再循环使用lowbit运算即可枚举该空位的可用数字


const int N = 9；
int row[N], col[N], cell[3][3];//记录行列与九宫格的状态
int ones[1 << N];

/***************为了加速，我们提前打好表************************************/
for(int i = 0 ;i < N ; i ++) maps[1 << i] = i;
//lowbit运算返回的是数值，而我们需要的是二进制数位中的1的位置
//maps[1(1)] = 0;maps[2(10)] = 1;maps[8(1000)] = 3

/*****************lowbit运算 lowbit（20（10100)=4（100）*******************/
inline int lowbit(int x)
{
    return x & -x;
}
/*****************求不同状态的交集，使用&运算即可***************************/
inline int get(int x, int y)
{
    return row[x] & col[y] & cell[x/3][y/3];
}
/*****************初始化状态，即二进制数位全部改为1*************************/
void init()
{
//初始化(1 << N) - 1的解释:
//1 << N = 512,再减1等于511,我们用二进制的运算看比较清楚:1000000000 - 1 = 111111111
    for(int i = 0; i < N; i ++) row[i] = col[i] = (1 << N) - 1;
    for(int i = 0; i < 3;  i ++)
        for(int j = 0; j < 3; j ++)
            cell[i][j] = (1 << N) - 1;
}


//具体使用

//1,修改第x行y列的空位状态
//假设在该位置上放置了数字t（1~9）
t -= 1;//我们需要映射到0~8
row[x] -= 1 << t;  //减去1<<t相当于在二进制数位上把第t个位置上的1改成0
col[y] -= 1 << t;
cell[x/3][y/3] -= 1 << t;

//2,枚举第x行y列的空位的可用数字
for(int i = get(x,y); i ; i -= lowbit(i))
{
    int t = maps[lowbit(i)]; //t就是可用的数字（0~8->1~9）
}