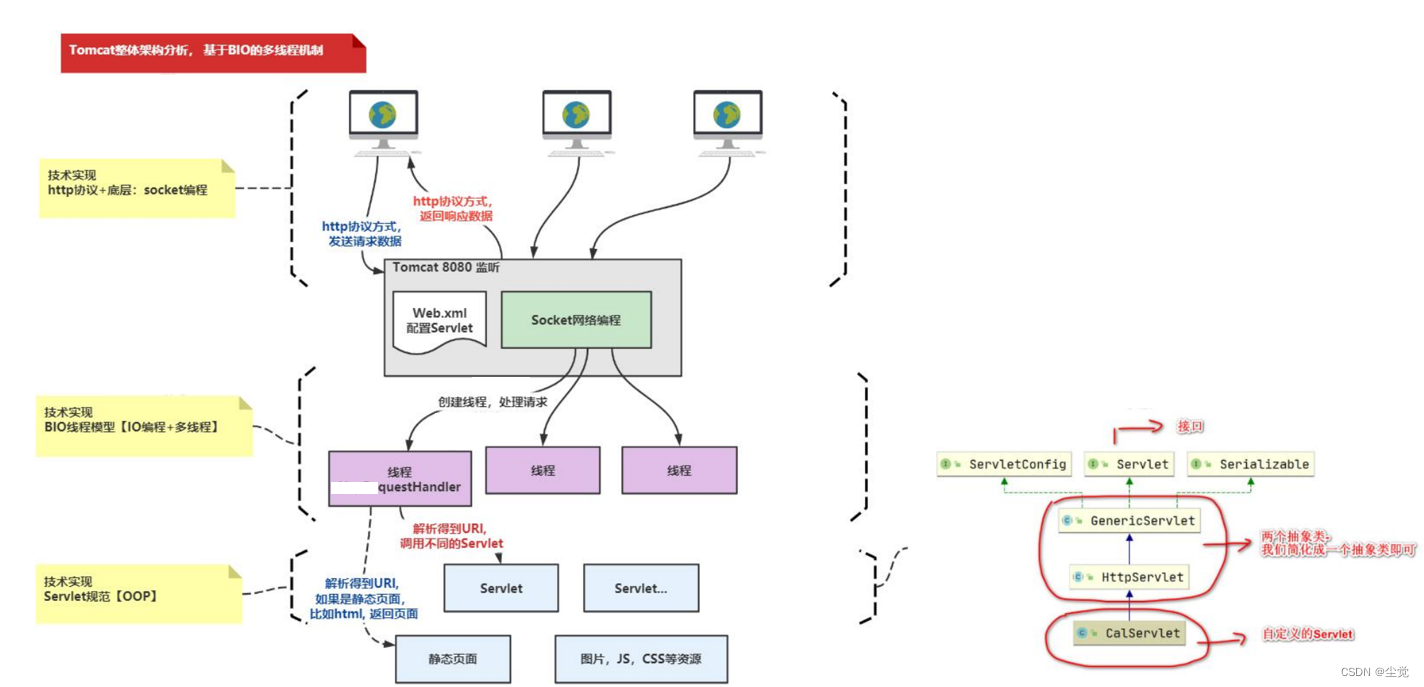
Problem - C - Codeforces

阿纳迪有一副多米诺骨牌。每张多米诺骨牌都有两个部分，每个部分都包含一些小点。对于每一个a和b，如1≤a≤b≤6，1≤a≤b≤6，正好有一块多米诺骨牌的一半是a点，另一半是b点。这组多米诺骨牌正好包含21张。下面是他的集合的精确图示：

另外，阿纳迪有一个没有自循环和多条边的无定向图。他想选择一些多米诺骨牌，把它们放在这个图形的边上。他最多可以使用每种类型的多米诺骨牌。每条边最多可以放一张多米诺骨牌。没有必要在图形的每条边上都放一张骨牌。

当把多米诺骨牌放在一条边上时，他也会选择其方向。换句话说，任何放置的多米诺骨牌的一半必须指向边缘的一个端点，另一半必须指向另一个端点。有一个问题：如果有多个半数的多米诺骨牌指向同一个顶点，每一个半数必须包含相同数量的点。

阿纳迪最多可以在他的图的边上放多少张多米诺骨牌？

输入
第一行包含两个整数n和m（1≤n≤7，1≤n≤7，0≤m≤n⋅(n-1)/2）--图中顶点和边的数目。

接下来的m行各包含两个整数。第i行的整数是ai和bi（1≤a，b≤n，1≤a，b≤n，a≠b，a≠b），表示有一条边连接着顶点ai和bi。

该图可能是断开的。然而，我们可以保证该图不包含任何自循环，并且任何一对顶点之间最多只有一条边。

输出
输出一个整数，表示Anadi可以在图的边上放置多米诺骨牌的最大数量。

例子
输入

4 4
1 2
2 3
3 4
4 1
输出

4
输入

7 0
输出

0
输入

3 1
1 3
输出

1
输入

7 21
1 2
1 3
1 4
1 5
1 6
1 7
2 3
2 4
2 5
2 6
2 7
3 4
3 5
3 6
3 7
4 5
4 6
4 7
5 6
5 7
6 7

产量

16
备注
这是第一个测试样本中的阿纳迪图的说明：

这里是将多米诺骨牌放在其每条边上的方法之一：

请注意，每个顶点所面对的多米诺骨牌的半数都有相同的点数。例如，所有面向顶点11的半边都有三个点。

题解:
如果点数小于7,边数一定全都可以放,任意两点只有一条边,每个点数不同,骨牌数一定可以满足

如果点数等于7,考虑最优,肯定会有两个点相同的,我们就枚举这两个点x,y,看他们,是否与另一个点z都有边,如果有,只能有一条边

 

#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
int mod = 1e9 + 7;
int d[10][10];
void solve()
{
	int n,m;
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		int a,b;
		cin >> a >> b;
		d[a][b] = 1;
		d[b][a] = 1;
	}
	if(n < 7)
	{
		cout << m;
		return ;
	}
	int ans = 1e9;
	for(int i = 1;i <= 7;i++)
	{
		for(int j = i + 1;j <= 7;j++)
		{
			int cnt = 0;
			for(int k = 1;k <= 7;k++)
			{
				if(d[i][k]&&d[k][j])
				cnt++;
			}
			ans = min(ans,cnt);
		}
	} 
	cout << m - ans;
}


signed main()
{
//	ios::sync_with_stdio(0);
//	cin.tie(0);cout.tie(0);
	int t = 1;
//	cin >> t;
	while(t--)
	{
		solve(); 
	}
}