概念

奇异值分解（singular value decomposition）是线性代数中一种重要的矩阵分解。奇异值分解在某些方面与对称矩阵或厄密矩阵基于特征向量的对角化类似。然而这两种矩阵分解尽管有其相关性，但还是有明显的不同。对称矩阵特征向量分解的基础是谱分析，而奇异值分解则是谱分析理论在任意矩阵上的推广。

假设 $M$ 是一个 $m\times n$ 的矩阵，其中的元素全部属于域 $K$，也就是实数域或复数域。如此则存在一个分解使得$$M=U\Sigma V^{\ast },$$其中 $U$ 是 $m\times m$ 阶酉矩阵；$\Sigma$ 是 $m\times m$ 阶非负实数对角矩阵；而 $V^{\ast }$，即 $V$ 的共轭矩阵，实数也可以写为 $V^T$，是 $n\times n$ 阶酉矩阵。这样的分解就称作 $M$ 的奇异值分解。$\Sigma$ 对角线上的元素 ${\Sigma }_{i,j}$ 即为 $M$ 的奇异值。

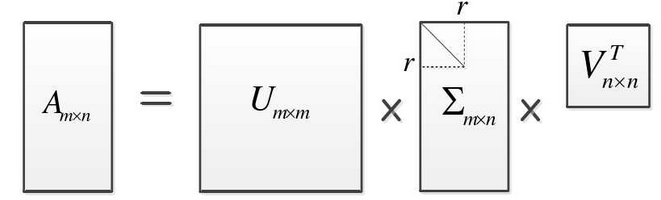
其直接解释为：
-$V$ 的行组成一套对 $M$ 的正交“输入”或“分析”的基向量。这些向量是 $M^{\ast }M$ 的特征向量；
-$U$ 的行组成一套对 $M$ 的正交"输出"的基向量。这些向量是 $M{M}^{\ast }$ 的特征向量；
-$\Sigma$ 对角线上的元素是奇异值，可以看作是输入与输出间进行的标量的“膨胀控制”。这些是 $M{M}^{\ast }$ 及 $M^{\ast }M$ 的特征值的非负平方根，并与 $U$ 和 $V$ 的行向量相对应。

奇异值和奇异向量，以及他们与奇异值分解的关系：

一个非负实数 $\sigma$ 是 $M$ 的一个奇异值仅当存在$K^m$ 的单位向量 $u$ 和 $K^n$ 的单位向量 $v$ 如下：$$Mv=\sigma uand{M}^{\ast }u=\sigma v.$$其中向量 $u$ 和 $v$ 分别为 $\sigma$ 的左奇异向量和右奇异向量。

对于任意的奇异值分解$$M=U\Sigma V^{\ast },$$矩阵 $\Sigma$ 的对角线上的元素等于M的奇异值. $U$ 和 $V$ 的列分别是奇异值中的左、右奇异向量。因此，上述定理表明：

• 一个 $m\times n$ 的矩阵至多有 $p=\min (m,n)$ 个不同的奇异值；
• 总能在 $K^m$ 中找到由 $M$的左奇异向量组成的一组正交基 $U$；
• 总能在 $K^n$ 找到由 $M$ 的右奇异向量组成的一组正交基 $V$。

如果对于一个奇异值，可以找到两组线性无关的左（右）奇异向量，则该奇异值称为简并的（或退化的）。

非退化的奇异值在最多相差一个相位因子 $\exp (i\varphi )$（若讨论限定在实数域内，则最多相差一个正负号）的意义下具有唯一的左、右奇异向量。因此，如果 $M$ 的所有奇异值都是非退化且非零，则除去一个可以同时乘在 $U$ , $V$ 上的任意的相位因子外， $M$ 的奇异值分解唯一。

根据定义，退化的奇异值具有不唯一的奇异向量。因为，如果 $u_1$ 和 $u_2$ 为奇异值 $\sigma$ 的两个左奇异向量，则它们的任意归一化线性组合也是奇异值 $\sigma$一个左奇异向量，右奇异向量也具有类似的性质。因此，如果 $M$ 具有退化的奇异值，则它的奇异值分解是不唯一的。

与特征值分解的联系：

奇异值分解能够用于任意 $m\times n$ 矩阵，而特征分解只能适用于特定类型的方阵，故奇异值分解的适用范围更广。不过，这两个分解之间是有关联的。给定一个 $M$ 的奇异值分解，根据上面的论述，两者的关系式如下：
$M^{\ast }M=V{\Sigma }^{\ast }{U}^{\ast }U\Sigma V^{\ast }=V({\Sigma }^{\ast }\Sigma )V^{\ast }$,
$M{M}^{\ast }=U\Sigma V^{\ast }V{\Sigma }^{\ast }{U}^{\ast }=U(\Sigma {\Sigma }^{\ast })U^{\ast }$,
关系式的右边描述了关系式左边的特征值分解。于是：

$V$ 的列向量（右奇异向量）是 $M^{\ast }M$ 的特征向量。
$U$ 的列向量（左奇异向量）是 $M{M}^{\ast }$ 的特征向量。
$\Sigma$ 的非零对角元（非零奇异值）是 $M^{\ast }M$ 或者 $M{M}^{\ast }$ 的非零特征值的平方根。

特殊情况下，当 $M$ 是一个正规矩阵（因而必须是方阵）根据谱定理，$M$ 可以被一组特征向量酉对角化，所以它可以表为：$$M=UD{U}^{\ast }$$其中 $U$ 为一个酉矩阵，$D$ 为一个对角阵。如果 $M$ 是半正定的，$M=UD{U}^{\ast }$ 的分解也是一个奇异值分解。
然而，一般矩阵的特征分解跟奇异值分解不同。特征分解如下：$$M=UD{U}^{-1}$$其中 $U$ 是不需要是酉的，$D$ 也不需要是半正定的。而奇异值分解如下： 　$$M=U\Sigma V^{\ast }$$其中 $\Sigma$ 是对角半正定矩阵，$U$ 和 $V$ 是酉矩阵，两者除了通过矩阵 $M$ 没有必然的联系。

几何意义

因为 $U$ 和 $V$ 都是酉的，我们知道 $U$ 的列向量 $u_1,...,u_m$ 组成了 $K^m$ 空间的一组标准正交基。同样，$V$ 的列向量 $v_1,...,v_n$ 也组成了 $K^n$空间的一组标准正交基（根据向量空间的标准点积法则）。

矩阵 $M$ 代表从 $K^n$ 到 $K^m$ 的一个线性映射 $\mathcal{T}$： $x\to Mx$。通过这些标准正交基，这个变换可以用很简单的方式进行描述： $\mathcal{T}(v_i)={\sigma }_i{u}_i,i=1,\dots ,\min (m,n)$，其中 ${\sigma }_i$ 是 $\Sigma$ 中的第 $i$ 个对角元。当 $i>\min (m,n)$ 时， $\mathcal{T}(v_i)=0$ 。

这样，SVD 分解的几何意义就可以做如下的归纳：对于每一个线性映射 $\mathcal{T}:K^n\to K^m$， $\mathcal{T}$ 的奇异值分解在原空间与像空间中分别找到一组标准正交基，使得 $\mathcal{T}$ 把 $K^n$ 的第 $i$ 个基向量映射为 $K^m$ 的第 $i$ 个基向量的非负倍数，并将 $K^n$ 中余下的基向量映射为零向量。换句话说，线性变换 $\mathcal{T}$ 在这两组选定的基上的矩阵表示为所有对角元均为非负数的对角矩阵。

应用

求广义逆阵（伪逆）
奇异值分解可以被用来计算矩阵的广义逆阵（伪逆）。若矩阵 $M$ 的奇异值分解为 $M=U\Sigma V^{\ast }$，那么M的伪逆为$$M^{+}=V{\Sigma }^{+}{U}^{\ast },$$其中 ${\Sigma }^{+}$ 是 $\Sigma$ 的伪逆，是将 $\Sigma$ 主对角线上每个非零元素都求倒数之后再转置得到的。求伪逆通常可以用来求解最小二乘法问题。

列空间、零空间和秩
奇异值分解的另一个应用是给出矩阵的列空间、零空间和秩的表示。对角矩阵 $\Sigma$ 的非零对角元素的个数对应于矩阵 $M$ 的秩。与零奇异值对应的右奇异向量生成矩阵 $M$ 的零空间，与非零奇异值对应的左奇异向量则生成矩阵 $M$ 的列空间。在线性代数数值计算中奇异值分解一般用于确定矩阵的有效秩，这是因为，由于舍入误差，秩亏矩阵的零奇异值可能会表现为很接近零的非零值。

矩阵近似值
奇异值分解在统计中的主要应用为主成分分析（PCA）。数据集的特征值（在SVD中用奇异值表征）按照重要性排列，降维的过程就是舍弃不重要的特征向量的过程，而剩下的特征向量张成空间为降维后的空间.

SVD 信号处理

SVD 信号处理过程主要分为三个步骤：矩阵建模与分解、分量选取、信号恢复。

矩阵建模与分解

由于奇异值分解的对象是矩阵，因此将 SVD 应用于信号处理时，如何将一维时间序列信号构造成二维空间矩阵形式至关重要。矩阵构造的方式有多种，如 Toeplitz 矩阵、Hankel 矩阵（重构吸引子轨迹矩阵的特例）、连续截断矩阵等。

Hankel 矩阵构造方式下的奇异值分解方法：
假设有一长度为 $L$ 的原始理想信号 $x=[x(1),x(2),...,x(L)]$，对此信号叠加噪声 $w=[w(1),w(2),...,w(L)]$ ，得到含噪信号 $y=[y(1),y(2),...,y(L)]$ ，它们之间的关系如下：$$\mathbf{y}=\mathbf{x}+\mathbf{w}$$根据含噪信号 $\mathbf{y}$ 构造的 Hankel 矩阵 $\mathbf{Y}$ 如下：$$Y=\left[\begin{array}{cccc}y(1)& y(2)& ...& y(n)\\ y(2)& y(3)& ...& y(n+1)\\ ⋮& ⋮& ⋮& ⋮\\ y(m)& y(m+1)& \dots & y(L)\end{array}\right]=X+W$$其中 $X$ 和 $W$ 分别为理想信号 $x$ 和噪声信号 $w$ 所构成的 Hankel 矩阵，且 $L=m+n-1,m\le n$ 且当 $m$ 与 $n$ 越接近时，对信号的处理效果越好。因此，当 $L$ 为偶数时，取 $m=L/2,n=L/2+1$，当 $L$ 为奇数时，则取 $m=(L+1)/2,n=(L+1)/2$。

设矩阵 $Y$ 行数为 $m$，列数为 $n$，且有 $m\le n$ ，对矩阵 $Y$ 进行 SVD 分解，有$$Y=US{V}^T=[u_1{u}_2\dots u_m][S_{m}O]\left[\begin{array}{c}{v}_1^T\\ v_2^T\\ ⋮\\ v_n^T\end{array}\right]$$其中 $S_m=diag({\sigma }_1,{\sigma }_2,...,{\sigma }_m),O\in R^{m\times (n-m)}$表示零矩阵。因此上式也可以写为：$$Y=[u_1{u}_2\dots u_m]\left[\begin{array}{cccc}{\sigma }_1& & & \\ & {\sigma }_2& & \\ & & \ddots & \\ & & & {\sigma }_m\end{array}\right]\left[\begin{array}{c}{v}_1^T\\ v_2^T\\ ⋮\\ v_n^T\end{array}\right]$$将 $Y$ 写成分量组合形式如下：$$Y=\sum _{i=1}^m{u}_i{\sigma }_i{v}_i^T.$$

可以通过定义一个函数来将信号转换成 Hankel 矩阵，函数如下：

function A=hankel(X,varargin)
	N=length(X);
	if (nargin==1)
		A=zeros(fix(N/2),N-fix(N/2)+1);
		for j=1:N-fix(N/2)+1
			A(:,j)=X(j:j+fix(N/2)-1);
		end
	else
		m=varargin{1};
		A=zeros(m,N-m+1);
		for j=1:N-m+1
			A(:,j)=X(j:j+m-1);
		end
	end

分量选取

分量矩阵选取的好坏直接关系到消噪效果和特征提取结果是否准确，选取的分量矩阵太少会使得信号失真严重，选取过多则会残留较多的噪声。如果能够选取合适的分量矩阵使得从分量矩阵中恢复后的信号信噪比越大越好，但实际情况中不可能将噪声完全消除，或多或少还残留有噪声带来的误差，只能尽量提高信噪比。
由理想信号 $x$ 构造的 Hankel 矩阵 $X$ 相邻两行只有一个数据不同，整个矩阵是一个病态矩阵，病态矩阵的特点就是前 $l$ 个奇异值较大，能量主要分布在前几个分量矩阵，而之后的奇异值则趋于零，$l$ 就是矩阵阵 $X$ 的秩。

由噪声 $w$ 构造的 Hankel 矩阵 $W$ 相邻两行虽然也只有一个数据不同，但它们之间却不相关，因此矩阵是一个满秩矩阵。噪声 $w$ 的自相关函数满足：$$R_{ww}(\tau )=\{\begin{array}{ll}{d}^2& \text{if }\tau =0\\ 0& \text{if }\tau \ne 0\end{array}.$$其中 $d$ 为噪声序列 $w$ 的标准差。当理想噪声严格满足上式时，所构造的 Hankel 矩阵的奇异值大小相等，且一般要比理想信号矩阵的奇异值小。

由含噪信号声 $y$ 构造的 Hankel 矩阵 $Y$ 的奇异值 ${\sigma }_i(Y)$ 与矩阵 $X$ 的奇异值 ${\sigma }_i(X)$ 和矩阵 W 的奇异值 ${\sigma }_i(W)$ 满足如下关系：$${\sigma }_i(x)\le {\sigma }_i(Y)\le {\sigma }_i(X)+{\sigma }_i(W)$$表明对含噪信号 $y$ 构造的 Hankel 矩阵 $Y$，其奇异值分布规律类似于矩阵 $X$ 的奇异值分布规律，其前 $r$ 个奇异值要远大于后面的 $m-r$ 个奇异值，由此可通过选取前 $r$ 个奇异值进行重构。

假设矩阵 $Y$ 的奇异值构成的序列为 $s=({\sigma }_1,{\sigma }_2,...{\sigma }_m)$ ，定义 $$b_i={\sigma }_i-{\sigma }_{i+1},i=1,2,...,m-1.$$则由构成的序列 $b=(b_1,b_2,...,b_{m-1})$ 为奇异值差分谱序列。根据差分谱序列最大点的序号，可以确定 $r$ 的值，由此可选取前 $r$ 个分量矩阵进行重构，即$$\hat{Y}=\sum _{i=1}^r{Y}_i=\sum _{i=1}^r{\sigma }_i{u}_i{v}_i^T$$写成矩阵形式有$$\hat{Y}=U_r{S}_r{V}_r^T$$其中 $U_r=[u_1{u}_2\dots u_r]\in R^{m\times r}$ 为左奇异矩阵 $U$ 的前 $r$ 列，$S_r=diag({\sigma }_1,{\sigma }_2,...{\sigma }_r)\in R^{r\times r}$ 为矩阵 $S$ 的前 $r$ 行和前 $r$ 列组成的分块矩阵，$V_r=[v_1{v}_2\dots v_r]\in R^{n\times r}$ 为右奇异矩阵 $V$ 的前 $r$ 列。同样可通过一个函数来自适应选取分量矩阵，函数如下：

function A=resvd(D) %输入原始信号的 Hankel 矩阵，输出重构矩阵
	[m,n]=size(D);
	[U,S,V]=svd(D);
	s=diag(S);b=zeros(min(m,n),1);
	for k=1:min(m,n)-1
		b(k)=s(k)-s(k+1);
	end
	[~,l] = max(b(:));
	A = zeros(size(D));%初始化
	for i =1:l
		A=A+S(i,i)*U(:,i)*V(:,i)';
	end

信号恢复

选取前 $r$ 个分量矩阵进行重构后得到的矩阵 $\hat{Y}$ 实际上是对含噪信号形成的矩阵 $Y$ 进行降秩处理得到的低秩矩阵。对理想信号 $x$ 的近似估计就可以从低秩矩阵 $\hat{Y}$ 中得到，这是因为低秩矩阵 $\hat{Y}$ 中包含了理想信号的绝大部分能量信号，根据矩阵构造方式利用简便法和平均法从分量矩阵中得到分量信号，选取适当的分量信号并累加以实现理想信号的近似估计。

由矩阵 $Y$ 进行 SVD 分解得到分量矩阵 $Y_i$ 并不具有 Hankel 矩阵的形式，因此对单独的某一分量矩阵进行信号恢复并无实际意义，也无法从中恢复出理想信号。然而由前 $l$ 个各分量矩阵重构得到的矩阵 $\hat{Y}$ 是理想信号矩阵 $X$ 的近似估计，因此可以从 $\hat{Y}$ 中得到对理想信号 $x$ 的近似估计。设 $\hat{Y}$ 与 $X$ 之间的误差为 $E$，则有$$\hat{Y}=X+E$$一般来说，$E$ 不具有 Hankel 矩阵结构形式。将上式中的矩阵 $\hat{Y},X,E$ 尾相连排列得到向量 $\tilde{y},\tilde{x},\tilde{e}$ ，有$$\tilde{y}=\tilde{x}+\tilde{e}$$可知 $\tilde{y},\tilde{x},\tilde{e}$ 均为长度 $m\times n$ 的向量，由于 $\tilde{e}$ 很小，因此有 $$\tilde{y}=\tilde{x}$$向量 $\tilde{x}$ 可由理想信号向量 $x$ 通过矩阵变换得到，即$$\tilde{x}=xM$$通过矩阵的逆变换可以从 $\tilde{x}$ 中恢复出理想信号 $x$ ，即$$x=\tilde{x}{M}^{+}$$其中 $M^{+}=(M^{T}M{)}^{-1}{M}^T\in R^{mn\times L}$ 称为 $M$ 的伪逆。$\tilde{y}=\tilde{x}$ 两边同时右乘矩阵 $M^{+}$ 并结合式 $x=\tilde{x}{M}^{+}$ 可得到理想信号 $x$ 的近似估计信号 $\hat{y}$,即$$\hat{y}=\tilde{y}{M}^{+}\approx x$$到此完成了从重构矩阵恢复出近似理想信号的过程。同样可通过一个函数从重构矩阵中恢复出信号，函数如下：

function y=rec(A) %从二维矩阵中恢复出一维信号
	[m,n]=size(A);L=m+n-1;M=zeros(L,m*n);
	for i=1:m
		for j=1:n
		M(i+j-1,(i-1)*n+j)=1;
		end
	end
	a=reshape(A',1,m*n);
	M1=M'/(M*M'); %也可用 MATLAB 自带函数求伪逆，M1=pinv(M)
	y=a*M1;

由于矩阵 $M$ 是一个稀疏矩阵，在计算伪逆矩阵 $M^{+}$ 时会大大增加处理时间，而采用平均法可有效缩短时间，因此在实际处理时，采用平均法来恢复信号，平均法的函数代码如下：

function y=arec(A)
	[m,n]=size(A); L=m+n-1; y=zeros(1,L);
	if m<n
		A=A'; [m,n]=size(A);
	end
	for j=1:n-1
		y(j)=0;
		for k=1:j
			y(j)=y(j)+A(k,j-k+1);
		end
		y(j)=y(j)/j;
	end
	for j=n:m
		y(j)=0;
		for k=1:n
			y(j)=y(j)+A(j-k+1,k);
		end
		y(j)=y(j)/n;
	end
	for j=m+1:m+n-1
		y(j)=0;
		for k=1:m+n-j
			y(j)=y(j)+A(j-n+k,n-k+1);
		end
	y(j)=y(j)/(m+n-j);
	end

参考

1. 维基百科：奇异值分解
2. 聂振国. 基于奇异值分解的信号处理关键技术研究[D].华南理工大学,2016.
3. 博客：奇异值分解
4. 博客：一文让你通俗理解奇异值分解