239.滑动窗口最大值
题目
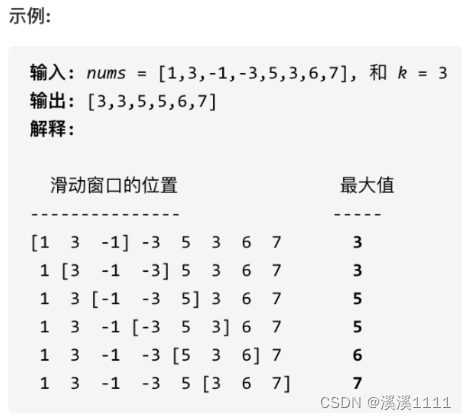
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
提示:
- 1 <= nums.length <= 10^5
- -10^4 <= nums[i] <= 10^4
- 1 <= k <= nums.length
方法
队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。
这个维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。
1.定义一个从队头到队尾递减的队列
2.输入k个元素,如果不满足递减原则则不加入队列中
3.每移动一个单位,如果滑动窗口移除的元素在队列中,则移除,不在队列中就不管了,然后加入元素看是否满足队列的条件,如果满足,则加入,否则不加入,队头元素即为所求(不弹出)
【有机会做一下单调栈】
代码
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var maxSlidingWindow = function(nums, k) {
class monoQueue {
queue;
constructor() {
this.queue = [];
}
enqueue(val) {
let back = this.queue[this.queue.length - 1];
while (this.queue.length && back < val) {
this.queue.pop();
// while循环时一定不要忘记更新值
back = this.queue[this.queue.length - 1]
}
this.queue.push(val);
}
dequeue(val) {
// this.front() 是定义数据结构的方法
// this.queue.pop() 是queue数组本身自带的方法
if (this.front() == val) {
this.queue.shift();
}
}
front() {
return this.queue[0];
}
}
let helpQueue = new monoQueue();
let resArr = [];
for (let i = 0;i < k;i++) {
helpQueue.enqueue(nums[i]);
}
resArr.push(helpQueue.front());
for (let i = k;i < nums.length;i++) {
helpQueue.enqueue(nums[i]);
helpQueue.dequeue(nums[i - k]);
resArr.push(helpQueue.front());
}
return resArr;
};
347.前k个高频元素
题目
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
- 输入: nums = [1,1,1,2,2,3], k = 2
- 输出: [1,2]
示例 2:
- 输入: nums = [1], k = 1
- 输出: [1]
提示:
- 你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
- 你的算法的时间复杂度必须优于 O ( n log n ) O(n \log n) O(nlogn) , n 是数组的大小。
- 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
- 你可以按任意顺序返回答案。
方法
思路很简单,大体分为三步
- 要统计元素出现频率(Map)
- 对频率排序(对频率进行排序,这里我们可以使用一种 容器适配器就是优先级队列)
- 找出前K个高频元素
优先级队列是一个披着队列外衣的堆,因为优先级队列对外接口只是从对头取元素,从队尾添加元素,再无其他取元素的方式,看起来就是一个队列
堆是一棵完全二叉树,树中每个结点的值都不小于(或不大于)其左右孩子的值。如果父亲结点大于等于左右孩子就是大顶堆,小于等于左右孩子就是小顶堆
使用大顶堆就要把所有元素都进行排序,那能不能只排序k个元素呢?
所以我们要用小顶堆,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素。
JS语言中没有堆这种数据结构,我们需要自己定义
排序算法(大顶堆还是小顶堆)
从队尾插入一个元素
删除堆顶元素
在本科时学了很多堆的理论,但之前用Java刷题时并没有涉及,现在给你一个实现那些理论的机会
Java直接给你定义好了
代码
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
class Heap {
constructor(compareFn) {
this.compareFn = compareFn;
this.queue = [];
}
push(val) {
this.queue.push(val);
let index = this.queue.length - 1;
let parent = Math.floor((index - 1) / 2);
while (parent >= 0 && this.compare(parent,index) > 0) {
[this.queue[index],this.queue[parent]] = [this.queue[parent],this.queue[index]];
//更新下标
index = parent;
parent = Math.floor((index - 1) / 2);
}
}
pop() {
const out = this.queue[0];
this.queue[0] = this.queue.pop();
// 下沉
let index = 0;
let left = 1;
// 选择左右两个子节点中小的那个(针对小顶堆而言)
let searchChild = this.compare(left,left + 1) > 0 ? left + 1 : left;
while (searchChild != undefined && this.compare(index,searchChild) > 0) {
[this.queue[index],this.queue[searchChild]] = [this.queue[searchChild],this.queue[index]];
//更新下标
index = searchChild;
left = 2 * index + 1;
searchChild = this.compare(left,left + 1) > 0 ? left + 1 : left;
}
return out;
}
size() {
return this.queue.length;
}
compare(index1,index2) {
if (this.queue[index1] == undefined) return 1;
if (this.queue[index2] == undefined) return -1;
return this.compareFn(this.queue[index1],this.queue[index2]);
}
}
var topKFrequent = function(nums, k) {
let heap = new Heap((a,b) => a[1] - b[1]);
let map = new Map();
for (let i = 0;i < nums.length;i++) {
map.set(nums[i],(map.get(nums[i]) || 0) + 1);
}
for (const entry of map.entries()) {
heap.push(entry);
if (heap.size() > k) {
heap.pop();
}
}
let resArr = [];
for (let i = k - 1;i >= 0;i--) {
resArr[i] = heap.pop()[0];
}
return resArr;
};