题目描述:
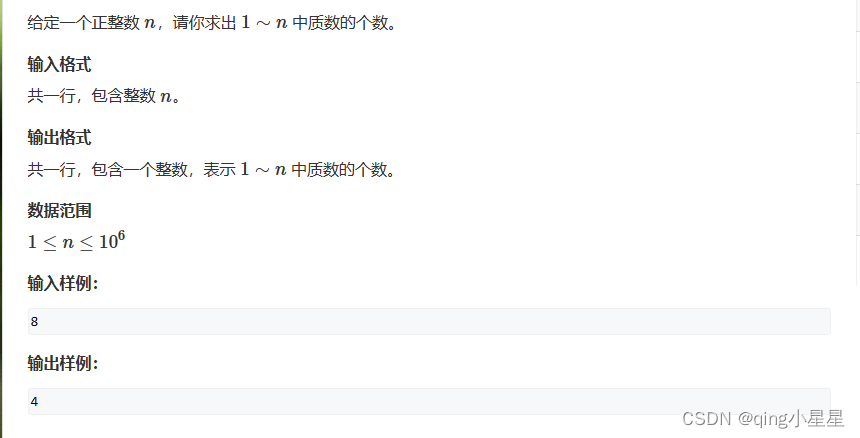
题目分析:
这道题可以用,朴素筛,埃氏筛,欧拉筛来写。
普通筛: 时间复杂度:O(n logn)
时间复杂度太高,会超时的!!(9/10)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int cnt;
const int N = 1e6+10;
int st[N], prime[N];
void get_primes()
{
for(int num = 2; num <= n; num++) //当前枚举到第i个数
{
int flag = 0;
for(int j = 2; j <= num/j; j++)
{
if(num % j == 0)
{
flag = 1;
break;
}
}
if(flag == 0)
cnt++;
}
}
int main(void)
{
cin>> n;
get_primes();
cout<< cnt << endl;
return 0;
}
埃氏筛: 时间复杂度:O(n lognlogn)
欧拉筛的原理:
从2开始打表,若2为质数,则2的倍数必然不是质数,因此便让表中的4 6 8 10…全部删除,最后剩下的就是素数。其运行速度要远高于普通筛。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int cnt;
const int N = 1e6+10;
int st[N], prime[N];
void get_primes()
{
for(int i = 2; i <= n; i++)
{
if( st[i] ) //如果i已经被筛掉了
continue;
prime[cnt++] = i;
for(int j = i+i; j <= n; j += i)
st[j] = true; //筛掉j
}
}
int main()
{
cin>> n;
get_primes();
cout<< cnt;
return 0;
}
欧拉筛: 时间复杂度:O(n)
i存的是最大质因数(非自己)
prime[j]存的是最小质因数
欧拉筛的原理:
在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。
利用:最小质因数*最大质因数(非自己) = 这个合数
若 i % primes[ j ] == 0 ,则说明 primes[ j ] 是 i 的最小质因子,那么primes[ j ] 也一定是primes[ j ] * i 的最小质因子。
若i % primes[ j ] != 0 ,由于我们是从小到大枚举的所有的质数,并且我们没有枚举到 i 的任何一个质因子,则此时primes[ j ] 一定小于 i 的所有质因子,但是primes[ j ] 也一定是primes[ j ] * i 的最小质因子。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int cnt;
const int N = 1e6+10;
int st[N], prime[N];
void get_primes()
{
for(int i = 2; i <= n; i++)
{
if( !st[i] ) prime[cnt++] = i;
for(int j = 0; prime[j] <= n/i; j++)
{
st[prime[j] * i] = true;
if(i % prime[j] == 0) //当i%primes[j]==0时,最小质因子就是primes[j]
break;
}
}
}
int main()
{
cin>> n;
get_primes();
cout<< cnt;
return 0;
}
对于 i%prime[j] == 0 就break的解释 :当 i是prime[j]的倍数时,i = kprime[j],如果继续运算 j+1,i * prime[j+1] = prime[j] * k prime[j+1],这里prime[j]是最小的素因子,当i = k * prime[j+1]时会重复,所以才跳出循环。
举个例子 :i = 8 ,j = 1,prime[j] = 2,如果不跳出循环,prime[j+1] = 3,8 * 3 = 2 * 4 * 3 = 2 * 12,在i = 12时会计算。因为欧拉筛法的原理便是通过最小素因子来消除。
祝我们都能天天快乐AC~