799. 最长连续不重复子序列 - AcWing题库

通常情况双指针就是需要将O(N^2^)，利用某些单调性质实现O(N)

通用代码模板

for(int i = 0 , j = 0; i < n ; i ++){
	while(j < i && check(i , j ) ) j ++;

	// 需要处理的逻辑
}

check判断是否构成

算法推导

题目中要求我们求

• 最长的
• 连续的
• 不重复子序列

问题一：为什么能想到使用双指针算法？

双指针算法适用于多种场景，其中之一就是在一个序列中寻找一个连续的空间

在本题中，我们可以使用指针i遍历整个序列，使用另一个指针j维护以i为右端点——最长的不重复的子序列。

既然知道这题我们需要使用 双指针算法 寻找一个连续子序列，所以我们就可以带入模板

确定判断条件

带入模板后，我们需要确定在什么样的情况下，j++——也就是想清楚，check函数的逻辑

我们重新审题，发现题目一共有三个条件：最长、连续、不重复。

使用双指针算法一定能让其连续，最长也可以通过设置比较res 和 （i到j的距离）得到最大值

所以这里的check函数的逻辑就是得到一个 不重复 的子序列！

问题二：如何判断该值是否在数组中出现过一次，是否重复？

这里我们想到的就是使用hash表进行判断，也就是在直接以输入的值作为key，每次遇到一次，对应的下标就+1

翻译成代码就是

s[ a[i] ] ++;

所以后续若我们需要判断是否重复过，只需要判断对应的a[i] 值是否大于1

我们来对输入样例数据1 2 2 3 5 来模拟一遍。

开始时，指针i和指针j同时指向第一个元素

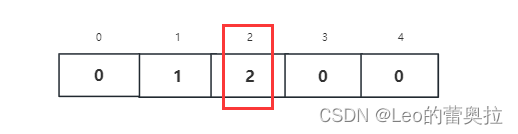
对应数组S的变化情况

判断当前s[a[i] ] = 1，不大于1

指针i指向下一个

对应数组S的变化情况

判断当前s[a[i] ] = 1，不大于1

i继续向后走

对应数组S的变化情况

判断当前s[a[i] ] = 2，大于1

所以此时需要将j++，对应记录的数组S就需要–了，因为子序列缩减了

因为数组S表示对应a[i]出现的次数

引申一下，就可以得到子序列的长度（因为子序列在遇到重复元素时是需要缩减的！）

指针J指向下标为1的位置，对应a[i] = 1的值减小

j继续向后走，对应值继续缩减

此时对应的数组S的值就不再>1，退出循环

此后就一直执行该判断，最后得到的结果如下

所以最后得到的最长子序列长度就是3了，对应计算就呼之欲出了res = max(res , i - j + 1)

表示当前res 和 i和j之间的距离的最大值

问题三：为什么这里要用循环进行判断，而不是直接使用if，然后将j = i ，不是更好吗？

第一点：我们是使用的是双指针算法，算法模板中就是while循环

第二点：我们需要一个一个的消除值，因为我们的区间在不断缩减。如果我们直接将j = i，其中a[i]值前面的S数组的值就不会被清空，在后续遇到时，可能非法触发！！！

例如这个例子

这里找到的最长子序列是

但是实际序列是

因为这里3和9都没有被清空，所以再一次遇到对应的s [ a[i] ]的值就会大于1，修改j的值

第三点：一般情况我们也是采用循环而不是判断，因为可能出现不同的情况，特别是对于这种前面的状态会影响后面的状态

解答代码

#include<iostream>

using namespace std;

const int N = 1e5+10;

int n , a[N] , s[N];

int main(){
    cin >> n;
  
    for(int i = 0 ; i < n ; i ++){
        cin >> a[i];
    }
  
    int res = 0;
  
    for(int i = 0 , j = 0 ; i < n ; i ++){
        s[a[i]] ++;
      
        while(s[a[i]] > 1){
            s[a[j]]--;
            j ++;
        }
      
        res = max(res , i - j + 1);
      
    }
    cout << res;
  
  
    return 0;
}