四舍五入大家都知道,但你知道银行家舍入法么?你知道JS里的toFixed实现用的是哪种吗?
前两天我写了篇《0.1 + 0.2 不等于 0.3?原来是因为这个》,大概就是说,0.1 + 0.2不等于0.3是因为浮点数精度问题。
结果在评论区看到一位热心网友的质疑:

我第一反应是,不会真讲错了吧?银行家舍位法又是什么?

本着对大家负责任的态度,我还是严谨的好好查了下相关知识,并迅速提取到本质区别,然后回复了这位网友:

我都被我的严谨和效率感动到了。

今天我就来给大家讲讲,什么是所谓的“银行家舍入法”。
银行家舍入法,其实是一种戏谑的叫法,专业名词是奇进偶舍[1],一种数值修约规则。
数值修约,是指在进行具体的数字运算前,按照一定的规则确定一致的位数,然后舍去某些数字后面多余的尾数的过程。
比如我们最常用的四舍五入[2]就是其中一种数值修约规则,其它常见的还有上取整(ceil),下取整(floor)等等。
那“奇进偶舍”的具体算法是什么样的呢?
其实用一句话就可以概括:四舍六入五成双。详细算法如下:
-
保留位数的后一位如果小于5,则舍去。
-
保留位数的后一位如果大于5,则进上去。
-
保留位数的后一位如果是5
-
且5后面仍有数,则无论奇偶都要进入。
-
若5后面不再有数,要根据尾数“5”的前一位决定: 如果是奇数则进入,如果是偶数则舍去。
-
举个例子:(以保留两位小数为例)
5.214 ≈ 5.21(4小于5)
5.216 ≈ 为5.22(6大于5)
5.2254 ≈ 5.23(5后面有数,进入)
5.215 ≈ 5.22(5后面没数,前一位1是奇数,进入)
5.225 ≈ 5.22(5后面没数,前一位2是偶数,舍弃)
复制代码目前,大部分编程语言都是默认使用“奇进偶舍”,比如C/C++、JavaScript、PHP、Go等。
既然如此,我们用前端最擅长的JS试试效果(对应的函数是toFixed):
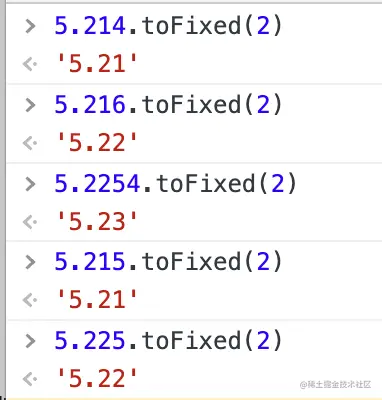
额……翻车了么?
5.215不是说好了约等于5.22么,怎么在JS这里变5.21了?发生了什么?

不用惊慌!其实这个问题我在上一篇《0.1 + 0.2 不等于 0.3?原来是因为这个》里就讲过了,就是浮点数精度问题导致的误差,我们可以来看看5.215到底是何方妖孽:

看到了没?
5.215底层竟然是5.214999……,那么此时按照奇进偶舍的规则,第三位4小于5直接舍弃,就成了5.21。
有意思吧?我之前讲的知识没白学吧哈哈(捏把汗,还好没误人子弟)。

好了,用法层面基本上讲完了。
不过大家是不是还有个疑问,为什么要采用这个修正规则呢?四舍五入这么简单粗暴的规则不香么?
因为从统计学的角度,“奇进偶舍”比“四舍五入”更为精确。
来,我们一起看下:
假设有5位储户的利息分别是0.000、0.001、0.002、0.003、0.004,这些厘被四舍五入了,因此银行赚了。但另外5位储户的利息分别是0.005、0.006、0.007、0.008、0.009,那么他们每人拿到的利息就是0.01,银行亏了。
而根据本福特定律[3]的相关测算,首位非零数字的出现是有概率分布的,数字越低概率越大。但非首位的数,基本符合随机分布。
那么上述10位储户的利息,经过四舍五入之后,银行的盈利情况如下:
0.000 + 0.001 + 0.002 + 0.003 + 0.004 - 0.005 - 0.004 - 0.003 - 0.002 - 0.001 = -0.005
复制代码银行亏了0.005!
这怎么能行!资本家的钱是你能轻易赚走的么?
而同样的数据,用“奇进偶舍”的规则计算后,刚好俩俩抵消,盈利为0,在这个案例几乎完美!
不过,并不是所有的案例都如此完美,但本福特定律从统计学层面已经很好的解释和规避了大部分情况下的误差。
当然不是零误差,只是让测量结果受到舍入误差的影响降到最低。
怎么样,今天你学废了么?