进行活性分析的动机
(1)在代码生成的讨论中,我们曾假设目标机器有无限多个(虚拟)寄存器可用,这简化了代码生成的算法,但对物理机器是个坏消息,因为机器只有有限多个寄存器,必须把无限多个虚拟寄存器分配到有限个寄存器中。
(2)这是寄存器分配优化的任务,需要进行活性分析。
引入示例
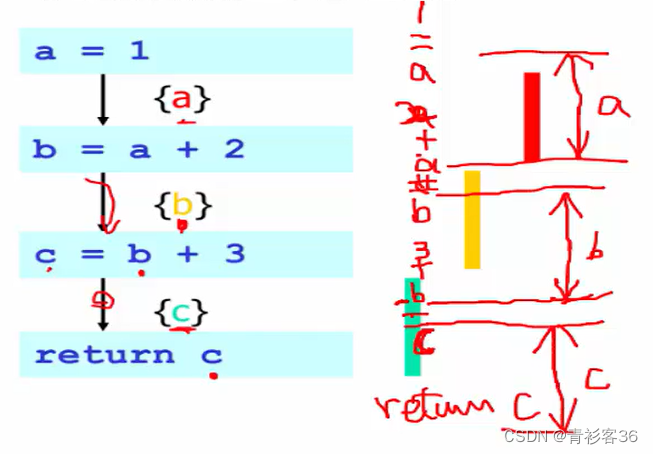
考虑这段三地址码:
a = 1
b = a + 2
c = b + 3
return c有三个变量a,b,c,假设目标机器上只有一个物理寄存器 r,那么是否可能把这三个变量同时放到寄存器 r 中?答案是肯定的,因为这三个变量可以分阶段的交替占用这个寄存器r。
计算在给定的程序点,哪些变量是“活跃”的(对应下图花括号中的变量),活跃信息给出了活跃区间的概念,活跃区间互不相交,所以三个变量可交替使用同一个寄存器。(把左侧的表达式竖着写(如下图),就可以清晰地体会区间交替、互不相交的含义了)
针对给定的这段三地址码,再结合上面分析的a、b、c三个变量的活跃区间情况,我们给出寄存器分配的映射表(寄存器分配优化中核心的数据结构,本质是哈希表),这样的寄存器分配的映射表指出a、b、c三个变量分别映射到哪个寄存器,就本例来说,三个变量映射到了同一个寄存器r。
有了这样的信息之后,我们可以根据这个分析,对三地址码进行重写(如下所示)
r = 1
r = r + 2
r = r + 3
return r由无限多个变量映射到有限个寄存器中的这个过程,叫做寄存器优化。
数据流方程
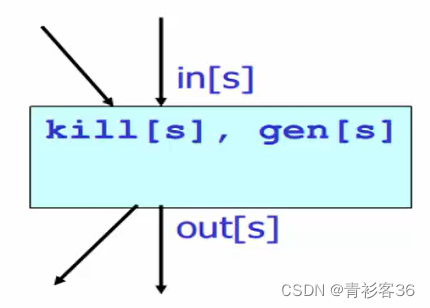
对任何一条语句:[ d : s ],给出两个集合
gen[ d : s ] = {x | 变量x在语句中被使用}
kill[ d : s ] = {x | 变量x在语句中被定义}
举个栗子:
x = y + z
z = z + xgen[1] = { y, z },kill[1] = { x }
gen[2] = {x, z},kill[2] = { z }
基本块内的后向数据流方程:

(注意与到达定义分析的区别,到达定义分析中的数据流是前向的)
由于是后向的,也就意味着先计算out再计算in,以下图为例,是从return c开始往上计算基本块内的后向数据流方程。注:下图中右侧计算的是每个数据块的in集合,彩色柱形代表三个变量对应的活跃区间。
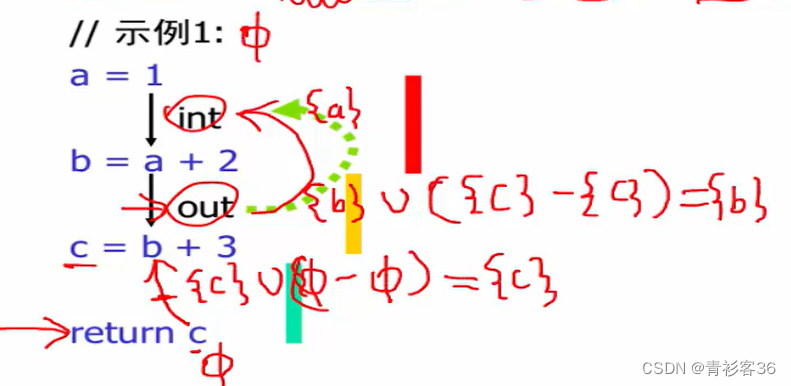
再来看一个例子,

我们通过观察可以得出,例2至少需要两个寄存器(a需要一个寄存器,b和c可以交替地使用同一个寄存器但要与a互斥)
下面由基本块内的数据流方程推广到一般的控制流图结构上来,即引出一般的数据流方程。
一般的数据流方程
方程(同样为后向的计算):

同样可以给出不动点算法:从初始的空集{}出发,循环到没有集合发生变化为止。
同样的举一个栗子,以下为一个一般的控制流图,一共有6条语句存在。
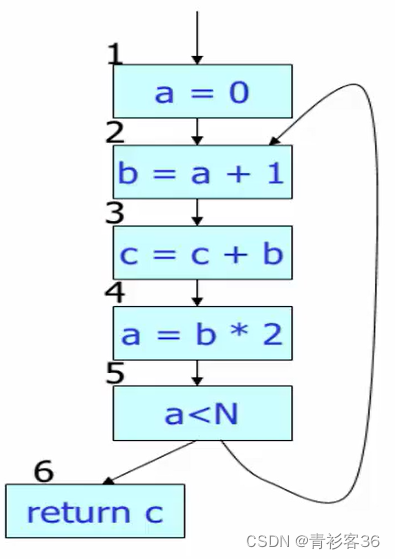
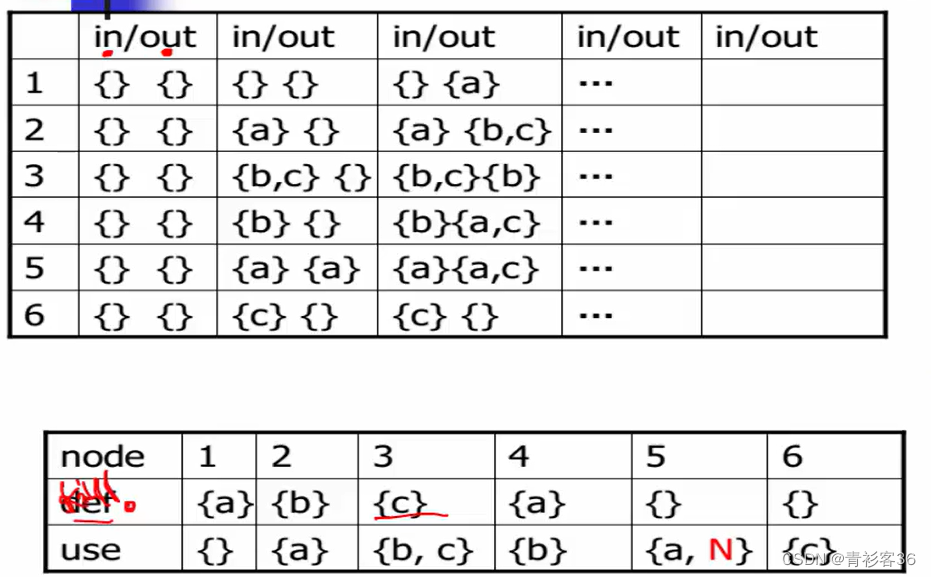
老师在PPT上演示的语句的遍历顺序是1,2,3,4,5,6,但是我感觉用逆拓扑序计算(即按6,5,4,3,2,1的顺序来计算in和out)更好理解,因为根据上面的公式,逆拓扑序计算out会把所有后继的in并起来算为自己
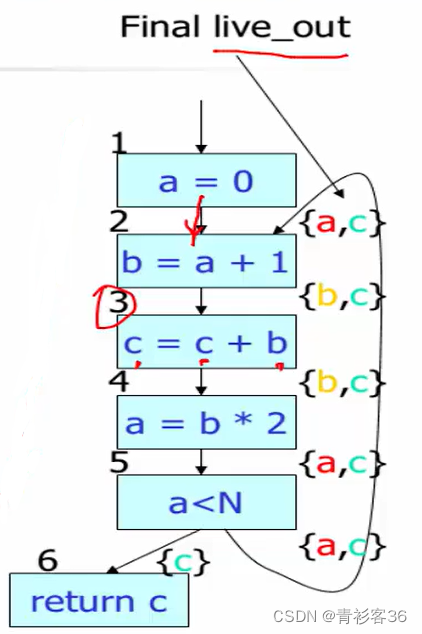
这是最终得到的live_out,比如在下面标红的边上,live_out就是{a, c},有了最终的live_out就能画出活跃区间图(如下所示)。
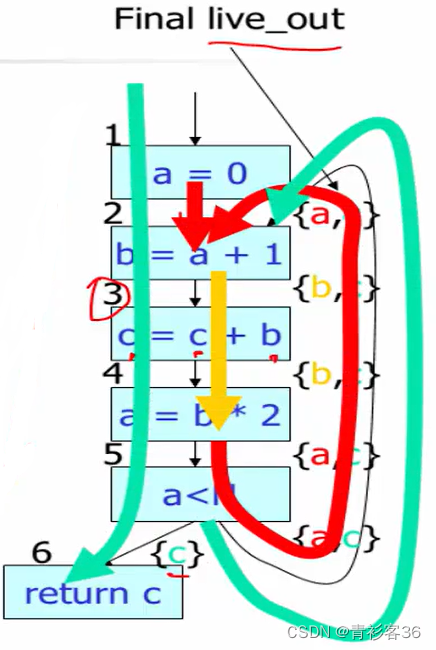
红色代表a的活跃区间,黄色代表b的活跃区间,绿色代表c的活跃区间
由此看出,a和b活跃区间不重叠,c与b和a都冲突(冲突的意思是,两个变量在同一点上都活着)
干扰图
干扰图是一个无向图G = (V, E):
1、对每个变量构造无向图G中一个节点
2、若变量x,y同时活跃,在x、y之间连一条无向边
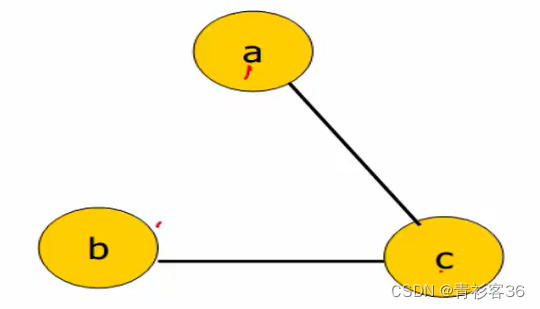
注:这是由上图得出的干扰图
干扰图清晰地描述了哪些变量是不能占用同一个寄存器的。比如a和c,在某个程序点处可能同时活着,他们两个的值是不同的,而且同时需要,所以a和c就需要两个寄存器进行存储(意味着a和c是相互冲突/干扰的)
此时笔者内心os:根据这个图,我怎么隐约感觉到在后续的寄存器分配中,会用到图染色算法呢,就是把寄存器当做不同的颜色来给这张图染色,且相邻点不同色。