1、超参数调试

在深度学习中，有各种各样的超参数，其中包括：学习率$\alpha$、动量超参数$\beta$、Adam中的超参数${\beta }_1$、${\beta }_2$和$\epsilon$、神经网络层数、每层的结点数量、 小样本数据集大小、学习率衰减的参数等等。

其中，学习率$\alpha$最为重要。

调试超参数，在不知道哪个超参数最为重要时，建议使用随机值进行探测。当给超参数取值时，也可以采用由粗糙到精细的策略：

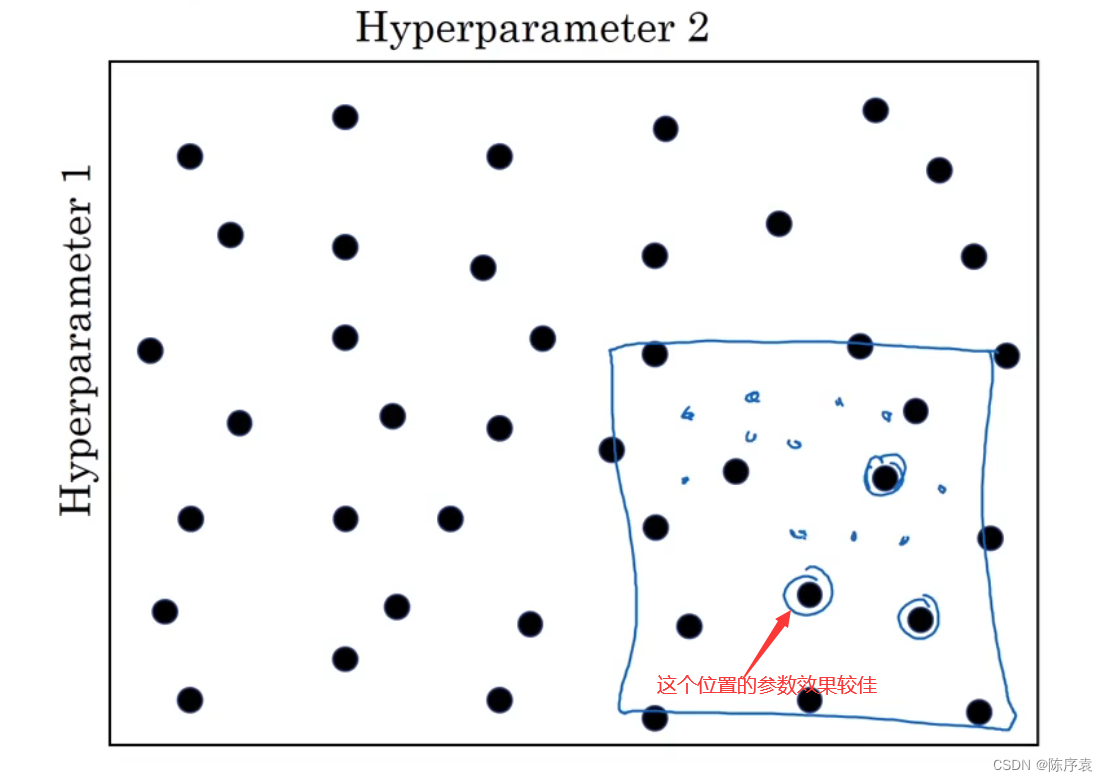
若发现有一点的参数效果较好，那么可以在它的附近范围内进行尝试，看是否能找到效果更好的参数点。

2、为超参数选择合适的范围

随机选取超参数值能够提升搜索效率，但随机取值并不是在有效值范围内进行随机均匀取值。

在一个较大的范围内，可以用对数标尺搜索超参数。

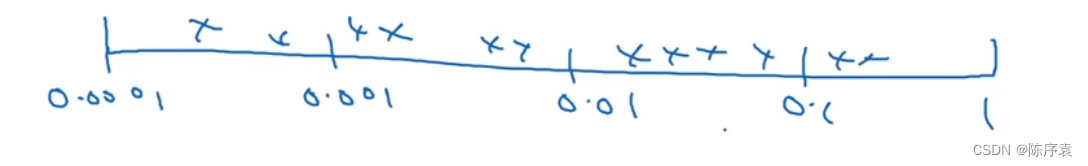
每个均匀范围内进行随机选取，代码：
r = -4 * np.random.rand()
learning_rate = np.power(learning_rate, r)

将r设为[-4,0]，那么学习率的搜索范围将为设置为0.0001到1.

其次，需要对$\beta$进行取值，操作方式与上述类似。

3、超参数训练的实践

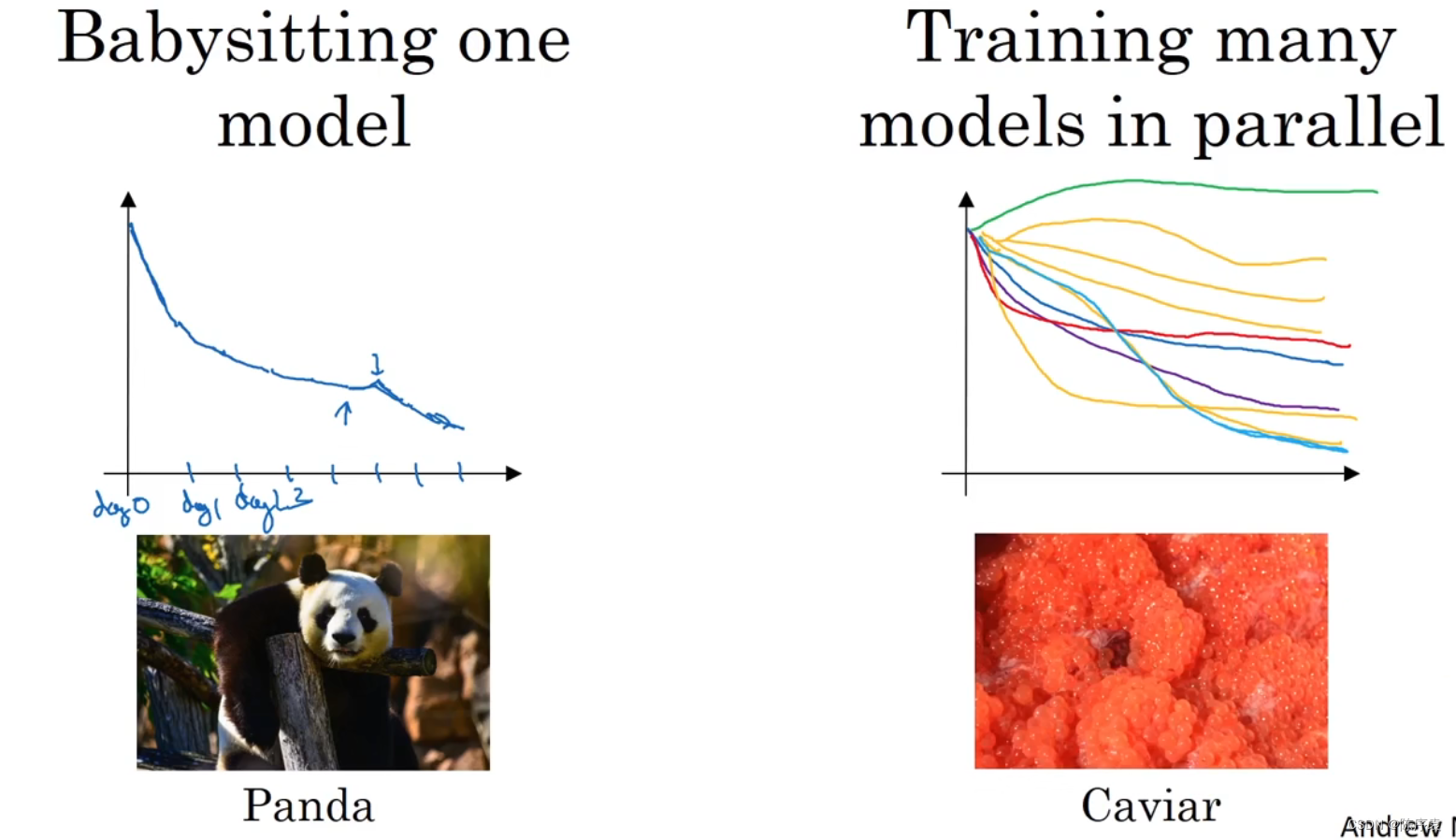
两种不同的超参数训练方式，左边的为只关注一个模型的参数对训练的影响，而右边的为同时关注多个模型的影响。
若具有足够的计算能力去平行试验许多模型，可以选择右边的。

每个超参数如果设置得不好，都会对训练产生巨大的负面影响，因此所有的超参数都要调整好，请问这是正确的吗？

【★】 错误
【 】 正确
We’ve seen in lecture that some hyperparameters, such as the learning rate, are more critical than others.

我们在视频中讲到的比如学习率这个超参数比其他的超参数更加重要。

4、正则化网络的激活函数

Batch归一化：在神经网络中已知一些中间值$z^1,...,z^n$，来自隐藏层。

计算第$i$个隐藏层数值的平均值：
$$\mu =\frac{1}{m}\sum _i{z}^i$$
方差：
$${\sigma }^2=\frac{1}{m}\sum _i(z_i-\mu {)}^2$$
标准差：
$$z_{norm}^i=\frac{z^i-\mu }{\sqrt{{\sigma }^2+\epsilon }}$$
$${\tilde{z}}^i=\gamma z_{norm}^i+\beta$$

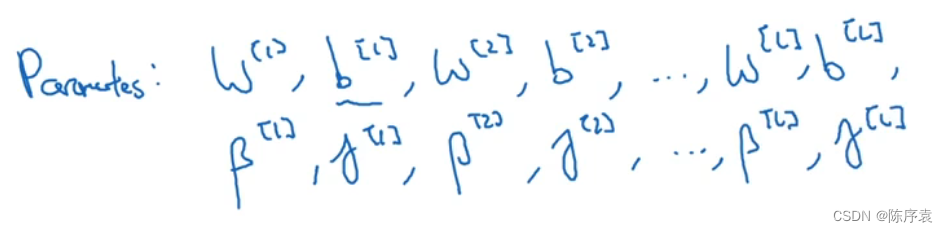
参数则在原来的基础上加上了正则化参数$\gamma$与$\beta$。

Batch归一化通常与mini-batch一起使用，

5、softmax回归

计算得到第$L$层的输出值$z^{[L]}=w^{[L]}{a}^{[L-1]}+b^{[L]}$，通过激活函数$t=e^{z^{[L]}}$放大每个节点的值，再通过$a_i^{[L]}=\frac{t_i}{{\sum }_{j=1}^4{t}_i}$计算每个节点的占比，得到预测的概率。

假如输入的是一张图片，那么输出的向量就代表该图片类别的预测概率。

判断Softmax函数的训练效果主要通过计算其损失函数：
$$L(\hat{y},y)=-\sum _{j=1}^4{y}_j\log {\hat{y}}_j$$
如$y=[0,1,0,0{]}^T$，而$\hat{y}=[0.3,0.2,0.1,0.4{]}^T$，该样本的训练效果就较差。