文章目录
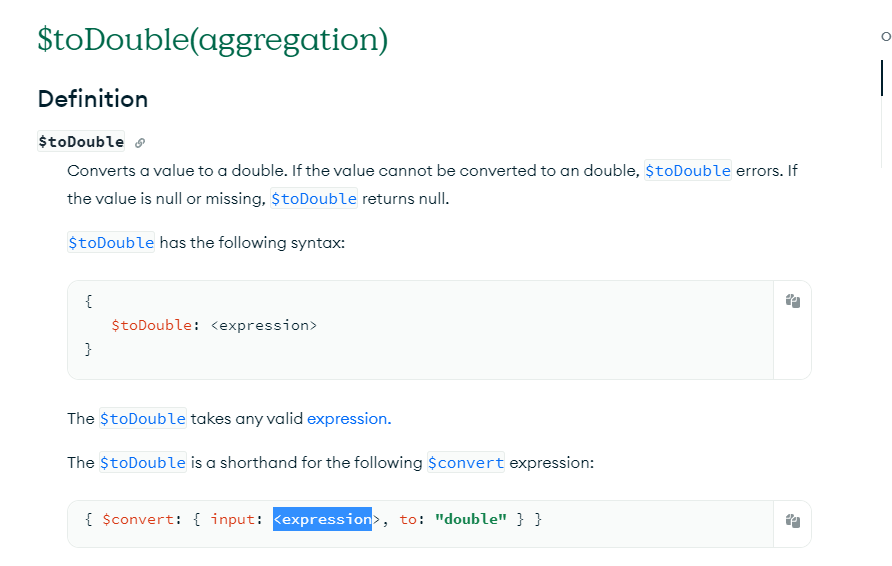
- Color Transfer Using Probabilistic Moving Least Squares
- 1. 颜色转换
- 2. 如何计算匹配点的概率
- 3. 核心思想和具体操作:
- 4. 特征点覆盖不到的颜色
- 4.1这里介绍一下引文7:
- 4.2. 分析
- 5. Probabilistic Moving Least Squares with Spatial Constraints for Nonlinear Color Transfer Between Images
- 6. 结果:
Color Transfer Using Probabilistic Moving Least Squares
1. 颜色转换
适用场景,配准后的图像有 密集的数量足够多的颜色匹配对。配准可以允许有一定的错误。
mlq这里不再多说,相比与mlq这篇文章主要考虑到匹配是否正确,
假如有很多匹配点,怎么知道一个匹配是否正确。是否可以计算该匹配点正确的概率。
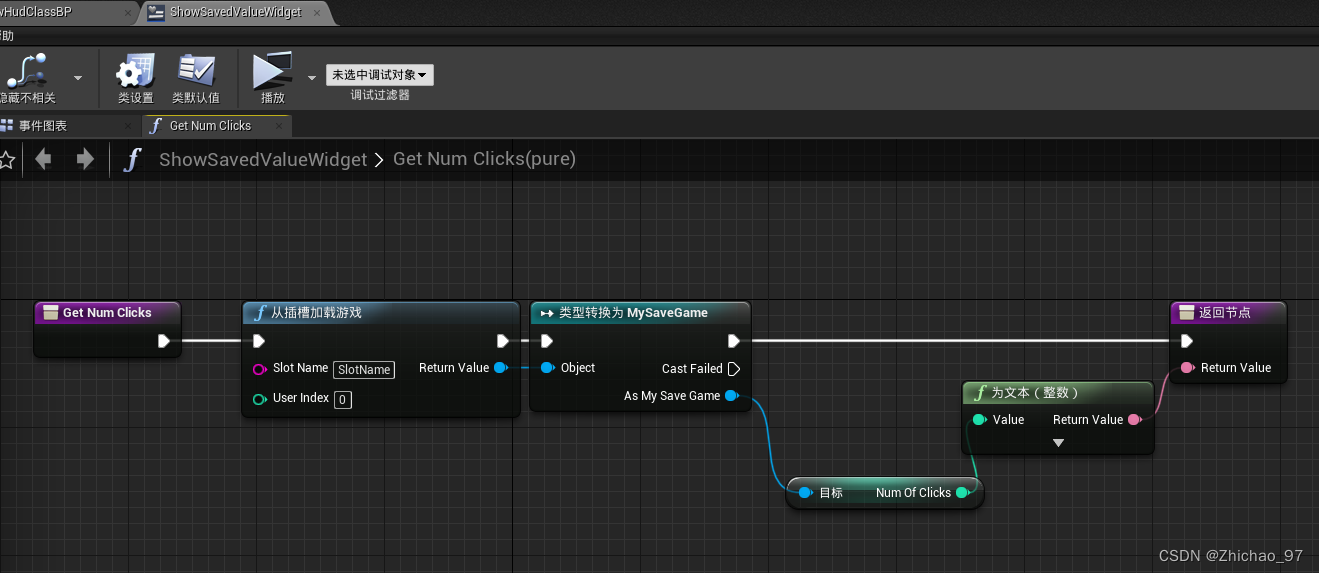
下图p_k就是匹配点的概率。将概率与w融合:得到新的weight


2. 如何计算匹配点的概率
1) 首先将rgb域用3Dlut 表示,比如
17
∗
17
∗
17
的
3
D
l
u
t
(
17
∗
17
∗
17
=
2197
)
17*17*17的3Dlut (17*17*17=2197)
17∗17∗17的3Dlut(17∗17∗17=2197)
2) 那么匹配的颜色落在对应格子的数量 和 总的匹配数量,可以表示为该匹配(i和j匹配)的 概率:
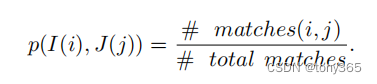
注意这里的i,j表示的grid index, 是 2197个格子之一。
其实第i个格子可能匹配到很多j, 第j个格子也可能匹配到很多i。
那么具体 i匹配j的概率是多少呢?用 2197 ∗ 2197 2197*2197 2197∗2197 的M邻接矩阵来表示,任意两个格匹配的概率。
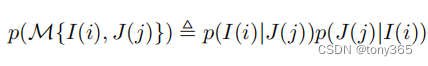
i 匹配为j的条件概率和 j 到i的条件概率:
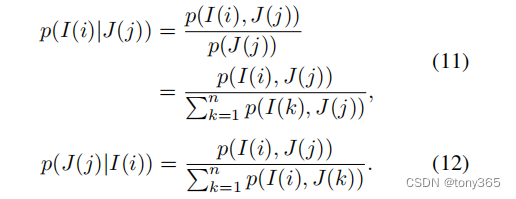
最终的矩阵就是:
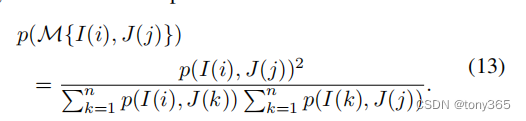
那么每个匹配的概率就可以查找最近的格子得到。
3. 核心思想和具体操作:
先配准,求概率

4. 特征点覆盖不到的颜色
用mlq效果不好,因为mlq本质是一个内插函数,外推效果不好。因此作者使用
[7] A. Ilie and G. Welch. Ensuring color consistency across multiple cameras. In ICCV, pages 1268–1275, 2005. 2, 5, 7
中的多项式插值函数,拟合出 空的grid (i)的对应的grid (j)。 利用已知的匹配点对。
4.1这里介绍一下引文7:
引文7主要介绍了一个标定方法:
标定的图像如下:左图包含了亮度变化,右图是常见的颜色。

标定方法是利用最小二乘求解 ccm, 或者利用文中提到的软件。
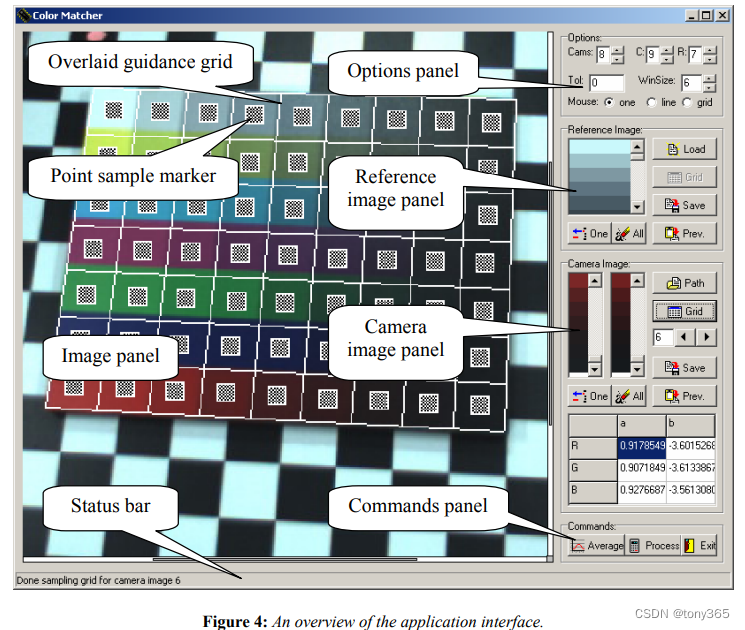
因此求出ccm后,每个颜色都可以找到对应的点 ,因此 可以填充3Dlut.
4.2. 分析
利用mlq, 但是又利用 多项式拟合, 那么多项式拟合之后 其实稍微优化一下就得到了3Dlut. 本身多项式拟合也是一种颜色转换。
5. Probabilistic Moving Least Squares with Spatial Constraints for Nonlinear Color Transfer Between Images
主要改进就是引入 空间域, local 域
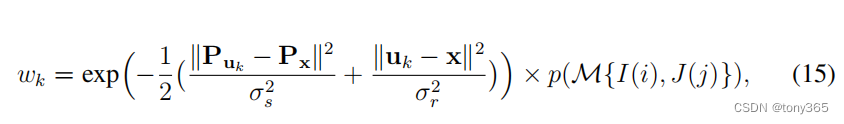

P是空间位置的距离。
6. 结果:
mls
pmls
b-pmls
b-pmls with extend