什么是树状数组

树状数组是一种用于维护数列前缀和的数据结构，它可以在 O(logn) 的时间复杂度内修改单个元素的值，以及查询某个区间的元素和。

树状数组的特点是什么？

• 树状数组的特点其实就是，在单点修改 ，和区间查询，它所需要写的代码量少，与时间复杂度低而闻名。
• 但是树状数组需要的空间复杂度很高，原因是，假如我们的查询的数字x的大小有100000这么大，那么这个树状数组的节点个数就得有100001个这么多。

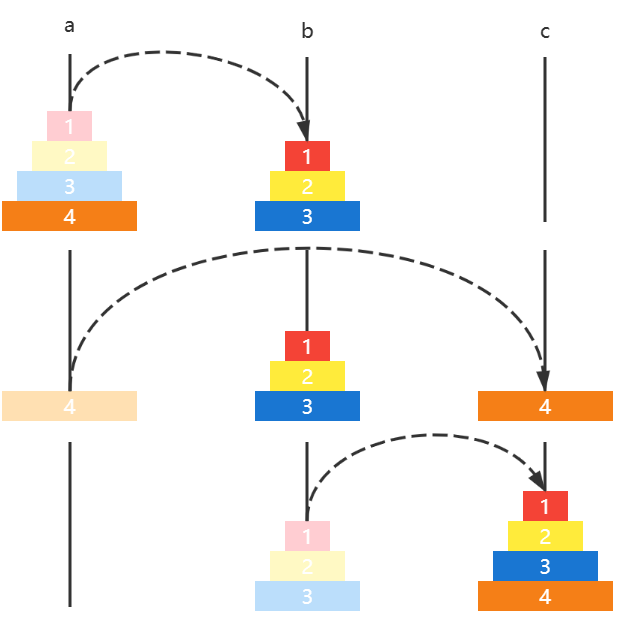
讲到这里，大家对树状数组大致上有了那么一丢丢了解。我们再来结合这张图，再来感受一下树状数组的工作原理。

树状数组的工作原理

• 最下面的八个方块代表原始数据数组 a。上面参差不齐的方块（与最上面的八个方块是同一个数组）代表数组 a 的上级——c 数组。

• c 数组就是用来储存原始数组 a 某段区间的和的，也就是说，这些区间的信息是已知的，我们的目标就是把查询前缀拆成这些小区间。

• 例如，从图中可以看出：

  • c_2 管辖的是 a[1 … 2]；
  • c_4 管辖的是 a[1 … 4]；
  • c_6 管辖的是 a[5 … 6]；
  • c_8 管辖的是 a[1 … 8]；
  • 剩下的 c[x] 管辖的都是 a[x] 自己（可以看做 a[x … x] 的长度为 1 的小区间）。

我们可以把a1到a8理解为一个有序的递增数列。它们的值也就是从1到8。

c1到c8，其实就是这个这个数列的树状数组。

管辖区间

不难发现，c[x] 管辖的一定是一段右边界是 x 的区间总信息。我们先不关心左边界，先来感受一下树状数组是如何查询的。

举例：计算 a[1…… 7] 的和。

过程：从 c7开始往前跳，发现 c7}只管辖 a7这个元素；然后找 c6，发现 c6管辖的是 a[5 … 6]，然后跳到 c4，发现 c4 管辖的是 a[1 … 4] 这些元素，然后再试图跳到 c0，但事实上 c0 不存在，不跳了。

那么问题来了，c[x](x >= 1) 管辖的区间到底往左延伸多少？也就是说，区间长度是多少？

树状数组中，规定 c[x] 管辖的区间长度为 2^k，其中：

• 设二进制最低位为第 0 位，则 k 恰好为 x 二进制表示中，最低位的 1 所在的二进制位数(最右边的第一个1所在的二进制位）；

• 2^k（c[x] 的管辖区间长度）恰好为 x 二进制表示中，最低位的 1 以及后面所有 0 组成的数。

• 举个例子，c88 管辖的是哪个区间？

  • 因为 88 = 01011000，其二进制最低位的 1 以及后面的 0 组成的二进制是 1000，即 8，所以 c88管辖 8 个 a 数组中的元素。

  • 因此，c88 代表 a[81 … 88] 的区间信息。

• 我们记 x 二进制最低位 1 以及后面的 0 组成的数为 lowbit(x)，那么 c[x] 管辖的区间就是 [x - lowbit(x) + 1, x]。

• 这里注意lowbit 指的不是最低位 1 所在的位数 k，而是这个 1 和后面所有 0 组成的 2^k。

那么问题又来了。怎么计算 lowbit？

• 根据位运算知识，可以得到 lowbit(x) = x & -x。
• 这一点，你可以参考原码，反码，补码的知识去看一下为什么是这样。
• 扫除盲点：教你清晰理解什么是计算机中的原码，反码，补码

代码实现：

int lowbit(int x) {
 	return x & -x;
}

区间查询

接下来我们来看树状数组具体的操作实现，先来看区间查询。

我们可以写出查询 a[1 … x] 的过程：

• 从 c[x] 开始往前跳，有 c[x] 管辖 a[x - lowbit(x) + 1 … x]；
• 令 x - lowbit(x)，如果 x = 0 说明已经跳到尽头了，终止循环；否则回到第一步。将跳到的 c 合并。
• 实现时，我们不一定要先把 c 都跳出来然后一起合并，可以边跳边合并。

比如我们要维护的信息是和，直接令初始 ans = 0，然后每跳到一个 c[x] 就 ans = ans + c[x]，最终 ans 就是所有合并的结果。

代码实现：

int getsum(int x) {  // a[1]..a[x]的和
  int ans = 0;
  while (x > 0) {
    ans = ans + c[x];
    x = x - lowbit(x);
  }
  return ans;
}

树状数组与其树形态的性质

在讲解单点修改之前，先讲解树状数组的一些基本性质，以及其树形态来源，这有助于更好理解树状数组的单点修改。

• 性质 1：对于 x <= y，要么有 c[x] 和 c[y] 不交，要么有 c[x] 包含于c[y]。

• 性质 2：在 c[x] 真包含于c[x +lowbit(x)]。

• 性质 3：对于任意 \x < y < x + lowbit(x)，有 c[x] 和c[y] 不交。

我们约定：

• l(x) = x - lowbit(x) + 1。即，l(x) 是 c[x] 管辖范围的左端点。
• 下面c[x] 和 c[y] 不交指 c[x] 的管辖范围和 c[y] 的管辖范围不相交，即 [l(x), x] 和 [l(y), y] 不相交。c[x] 包含于 c[y]等表述同理。

有了这三条性质的铺垫，我们接下来看树状数组的树形态（请忽略 a 向 c 的连边）。

事实上，树状数组的树形态是 x 向 x + lowbit(x) 连边得到的图，其中 x + lowbit(x) 是 x 的父亲。

注意，在考虑树状数组的树形态时，我们不考虑树状数组大小的影响，即我们认为这是一棵无限大的树，方便分析。实际实现时，我们只需用到 x <= n 的 c[x]，其中 n 是原数组长度。

单点修改

现在来考虑如何单点修改 a[x]。

• 我们的目标是快速正确地维护 c 数组。为保证效率，我们只需遍历并修改管辖了 a[x] 的所有 c[y]，因为其他的 c 显然没有发生变化。

• 管辖 a[x] 的 c[y] 一定包含 c[x]（根据性质 1），所以 y 在树状数组树形态上是 x 的祖先。因此我们从 x 开始不断跳父亲，直到跳得超过了原数组长度为止。

• 设 n 表示 a 的大小，不难写出单点修改 a[x] 的过程：

  • 初始令 x’ = x。
  • 修改 c[x’]。
  • 令 x’ = lowbit(x’)，如果 x’ > n 说明已经跳到尽头了，终止循环；否则回到第二步。

区间信息和单点修改的种类，共同决定 c[x’] 的修改方式。下面给几个例子：

• 若 c[x’] 维护区间和，修改种类是将 a[x] 加上 p，则修改方式则是将所有 c[x’] 也加上 p。
• 若 c[x’] 维护区间积，修改种类是将 a[x] 乘上 p，则修改方式则是将所有 c[x’] 也乘上 p。
• 然而，单点修改的自由性使得修改的种类和维护的信息不一定是同种运算，比如，若 c[x’] 维护区间和，修改种类是将 - a[x] 赋值为 p，可以考虑转化为将 a[x] 加上 p - a[x]。如果是将 a[x] 乘上 p，就考虑转化为 a[x] 加上 a[x] * p - a[x]。

下面以维护区间和，单点加为例给出实现。

void add(int x, int k) {
  while (x <= n) {  // 不能越界
    c[x] = c[x] + k;
    x = x + lowbit(x);
  }
}

总结

树状数组是一种用于维护数列前缀和的数据结构，它可以在 O(logn) 的时间复杂度内修改单个元素的值，以及查询某个区间的元素和。

至于为什么要学习这种数据结构，我的回答是，我在做leetcode算法题的时候，遇到类似问题了。而树状数组，是其中的一种解决方案，所以我就去特地学习了一下，并且得出了这么一篇文章。如果想要了解树状数组的更多知识了话，推荐大家去看这位大佬的文章：树状数组

这位大佬的语言比较高深，数学基础不好的人，不太容易看的懂。我这篇文章也是把这位大佬的文章截取一部分下来，做为我的文章。希望大家能够看得懂，并且学会什么叫做树状数组。

• 最后的最后，如果大家觉得我这篇文章写的好的话，请关注我，给我个赞和收藏，您的支持，是我持续输出优质内容的无上动力！