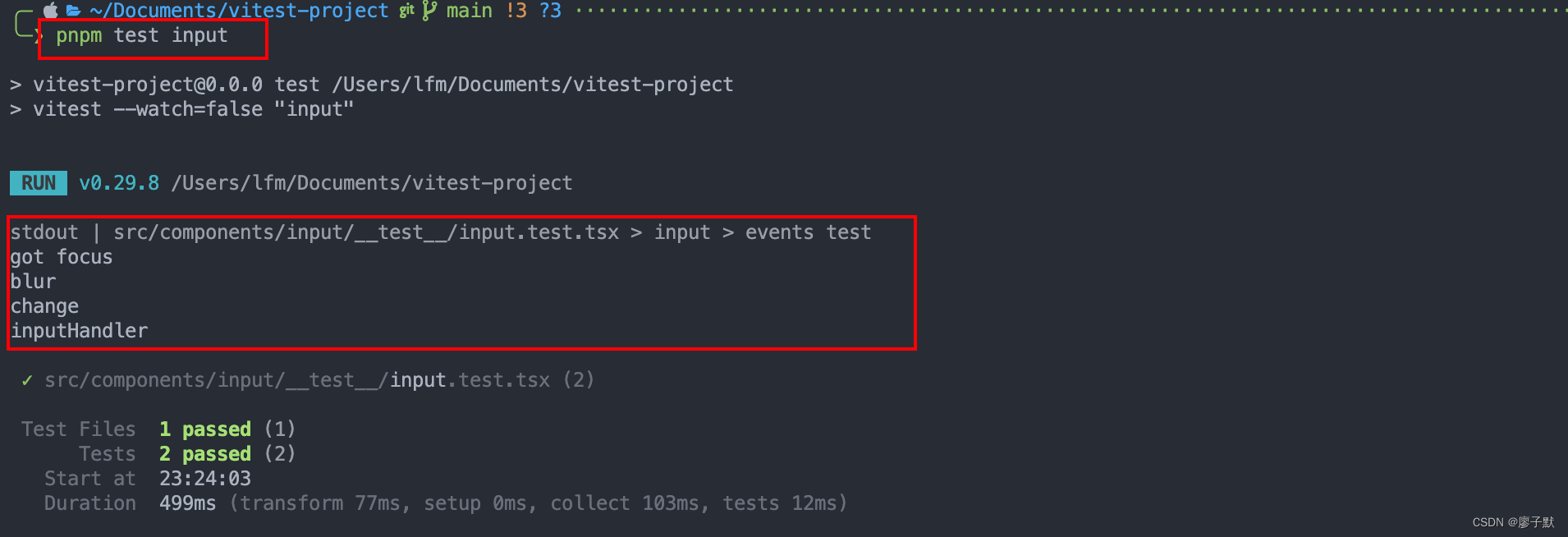
文章目录
- 第一部分:问题描述
- 1.1 题目
- 1.2 示例
- 🍀 示例一
- 🍀 示例二
- 1.3 提示
- 第二部分:思路分析
- 第三部分:代码实现
第一部分:问题描述
1.1 题目
🏠 链接:面试题 08.06. 汉诺塔问题 - 力扣(LeetCode)
⭐ 难度:简单
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
- 每次只能移动一个盘子;
- 盘子只能从柱子顶端滑出移到下一根柱子;
- 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
1.2 示例
🍀 示例一
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
🍀 示例二
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
1.3 提示
A中盘子的数目不大于14个。
第二部分:思路分析
假设每根柱子标号 a,b,c,每个圆盘用 1,2,3 … 表示其大小,圆盘初始在 a,要移动到的目标是 c
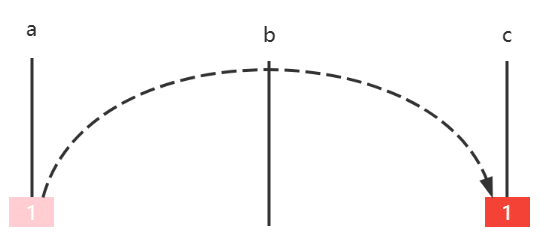
1️⃣ 移动一个圆盘
如果只有一个圆盘,此时是最小问题,可以直接求解
- 移动圆盘1 a ↦ c a \mapsto c a↦c
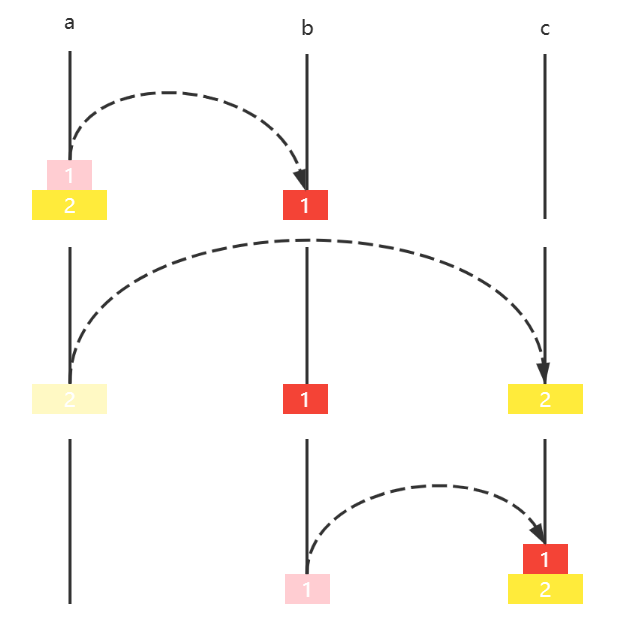
2️⃣ 移动两个圆盘
如果有两个圆盘,那么
- 圆盘1 a ↦ b a \mapsto b a↦b
- 圆盘2 a ↦ c a \mapsto c a↦c
- 圆盘1 b ↦ c b \mapsto c b↦c
3️⃣ 移动三个圆盘
如果有三个圆盘,那么
- 圆盘12 a ↦ b a \mapsto b a↦b
- 圆盘3 a ↦ c a \mapsto c a↦c
- 圆盘12 b ↦ c b \mapsto c b↦c

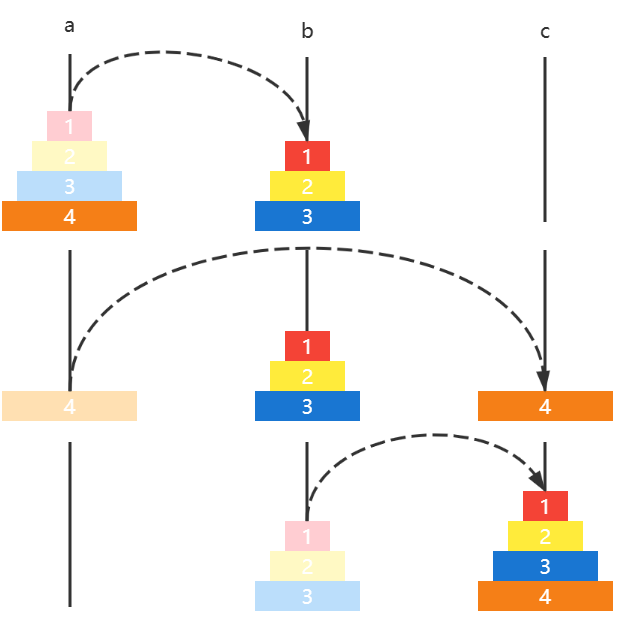
4️⃣ 移动四个圆盘
如果有四个圆盘,那么
- 圆盘 123 a ↦ b a \mapsto b a↦b
- 圆盘 4 a ↦ c a \mapsto c a↦c
- 圆盘 123 b ↦ c b \mapsto c b↦c
因此,如果有n个圆盘,那么
- 圆盘 1~(n-1) a ↦ b a \mapsto b a↦b
- 圆盘 n a ↦ c a \mapsto c a↦c
- 圆盘 1~(n-1) b ↦ c b \mapsto c b↦c
而 n-1 个圆盘如何移动呢,重复父问题的操作即可。
第三部分:代码实现
class Solution {
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
recursion(A.size(), A, B, C);
}
private void recursion(int n, List<Integer> A, List<Integer> B, List<Integer> C) {
// 先判断需要移动的圆盘数 n 是否为 0
if (n == 0) {
return;
}
// 将 n-1 个圆盘借助 C 从 A 移动到 B
recursion(n - 1, A, C, B);
// 将 第 n 个圆盘从 A 移动到 C
C.add(A.remove(A.size() - 1));
// 将 n-1 个圆盘借助 A 从 B 移动到 C
recursion(n - 1, B, A, C);
}
}









![[pgrx开发postgresql数据库扩展]2.安装与开发环境的搭建](https://img-blog.csdnimg.cn/img_convert/5532f1f571da5d6ccc54a556a30a4d5f.webp?x-oss-process=image/format,png)