在上一篇文章中我已经接触并认识了几个常用的集合函数：foreach,sorted,sortBy,sortWith,flatten,map,flatMap。

接下来在这一篇文章中我将继续学习剩下的几个集合函数。

一，filter函数

编辑练习题1：如何过滤出大于2的奇数？

练习题2：如何通过fliter和三元运算符过滤出大于2的奇数？

二，reduce函数及reduceLeft函数

1，reduce：无嵌套的列表：只是一个列表集合序列

2，reduce：嵌套有对偶元组的列表：列表里面嵌套对偶元组

3，reduceLeft：无嵌套的列表

三，reduceRight函数

四，fold函数及foldLeft函数

五，foldRight函数

六，aggregate函数及par函数

1，非并行集合使用aggregate函数

2，并行集合使用aggregate函数

一，filter函数

filter翻译为过滤，过滤器，所以filter函数就是用来过滤集合序列中的元素的。例如，现在我想要获取该数据结构中的偶数：

那么我就可以如下编写：

scala> val im_list=List(1,2,8,10)  // 列表集合序列
im_list: List[Int] = List(1, 2, 8, 10)

scala> im_list.filter(f=>f%2==0)   // 过滤出偶数
res0: List[Int] = List(2, 8, 10)

如上，我向filter函数中传入了一个参数f，并且该参数f代表列表中的每一个元素1，2，8，10

但是如果我的元素是在嵌套的集合序列中又该怎么过滤出偶数？如下数据：

scala> val list_arr=List(Array(1,2,8),Array(10))  // 列表集合序列中嵌套了数组集合序列

我记起之前学过的嵌套集合如果想要得到里面的元素的话得先要进行扁平化操作，于是我先使用了flatten函数对该数据结构进行扁平化操作：

扁平化之后的数据是及其可爱的，现在我就可以对其进行过滤操作（过滤出偶数）：

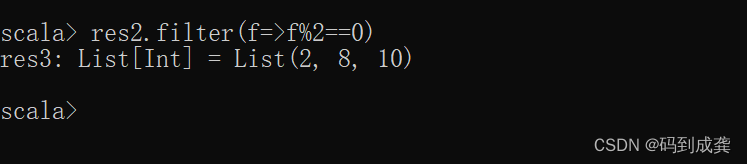练习题1：如何过滤出大于2的奇数？

要处理的集合序列（列表中嵌套列表）:List(List(1,2,8),List(10,12,15))

scala> val list_list=List(List(1,2,8),List(10,12,15))  // 列表嵌套列表

现在我去过滤出大于2的奇数：

scala> list_list.flatten.filter(f=>f%2!=0&&f>2)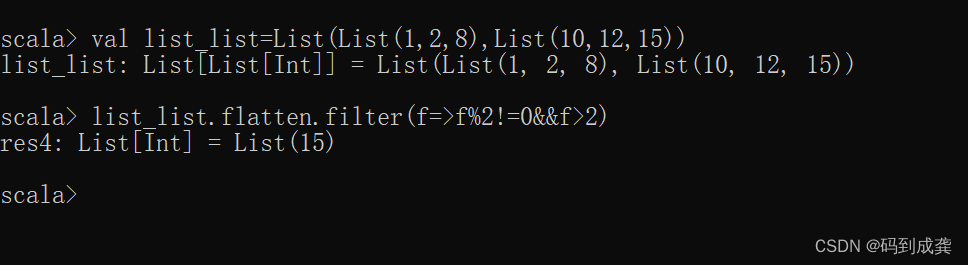

如上，我就过滤出了在集合序列中大于2的奇数：15

练习题2：如何通过fliter和三元运算符过滤出大于2的奇数？

在Scala中其实是没有三元运算符这种概念的，但是Scala也能够通过

if （条件） true else false实现三元运算符的功能，现在我将其和filter结合起来一起用：

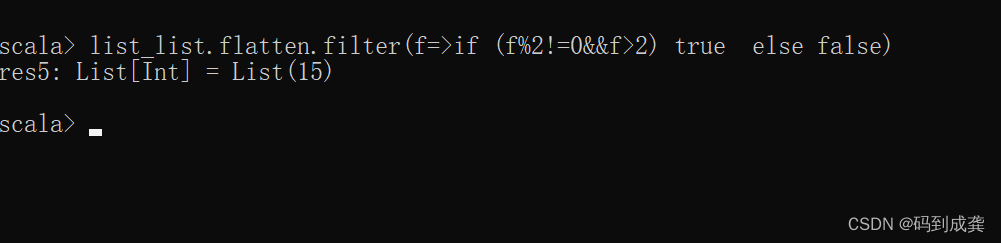
如上也可以得到结果。

二，reduce函数及reduceLeft函数

reduce函数需要我传入对偶元组，并且对偶元组中的两个参数分别代表集合序列中的第一个及后面的元素。这么一说可能有点抽象，但是使用代码敲出来效果之后就会形象许多。

1，reduce：无嵌套的列表：只是一个列表集合序列

待处理的集合序列：List(1,2,8,10)

scala> val im_list=List(1,2,8,10)

接下来使用reduce函数来对该集合序列进行求和：

scala> im_list.reduce((a,b)=>a+b)  // 使用reduce函数并让元素之间相加得到元素和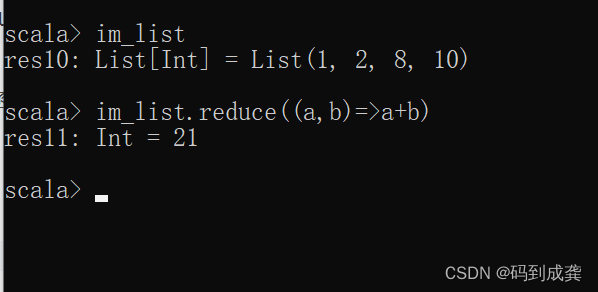

这个时候我又想到了之前还有一个列表和数组都有的求和函数sum，使用它也能得到一样的结果：

scala> im_list.sum   // 调用求和函数

现在我想要知道reduce中的a和b都分别是什么数字，那么就可以在函数里面加一条打印语句（在加上打印语句时，需要使用花括号将打印语句和运算表达式包裹起来，并且需要注意的是最好每一句都换行，别写在同一行，不然就会报错）:

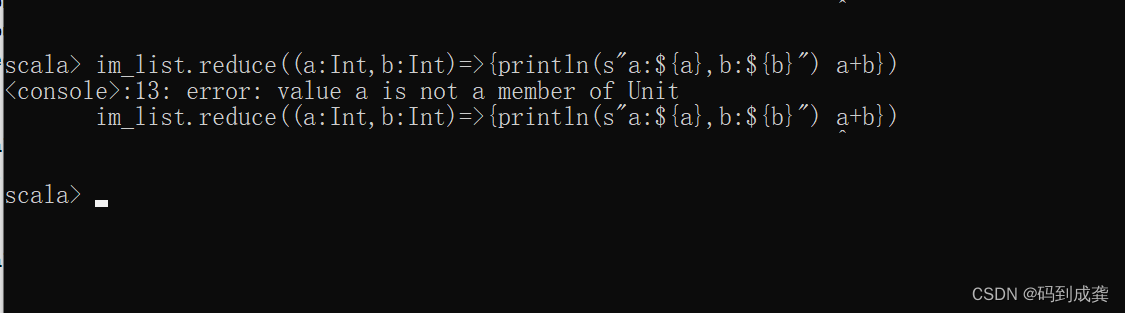
如下编写代码才会正确：

scala> im_list.reduce(   // 调用reduce函数
     | (a,b) => {        // 传入一个对偶元组
     | println(s"a=${a},b=${b}")   // 打印对应的a和b
     | a+b})             //  a和b要进行的运算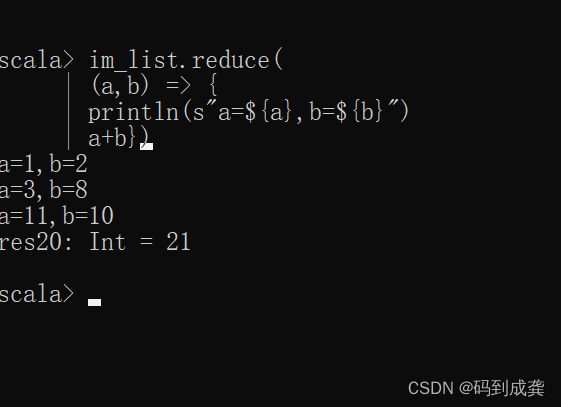

如上，我可以看到，当我们使用了reduce函数来求集合序列中的元素和时，a只会是两个值：一个是集合序列中的第一个元素，其他都是a与b通过表达式得到的值，因为集合序列中的第一个元素被a拿走了，所以b的值只会从集合序列中的第二个元素开始取。

在上式中，使用了a+b的表达式，所以a的值就会是a(a=1,3,11)与b（b=2,8,10）相加的结果。

在使用了reduce函数之后必须要有返回值，如上，我的返回的值为a+b即a最后的值为a+b的值。

并且，对于reduce函数来说，它的返回值类型和传入的参数类型必须保持一致，不然就会报错：

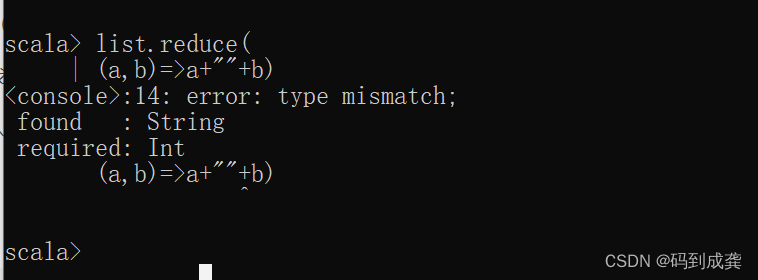
如上，因为返回值是字符串，但是传入的参数都是int类型（整数类型）的，所以就会提示提示我类型不匹配。

2，reduce：嵌套有对偶元组的列表：列表里面嵌套对偶元组

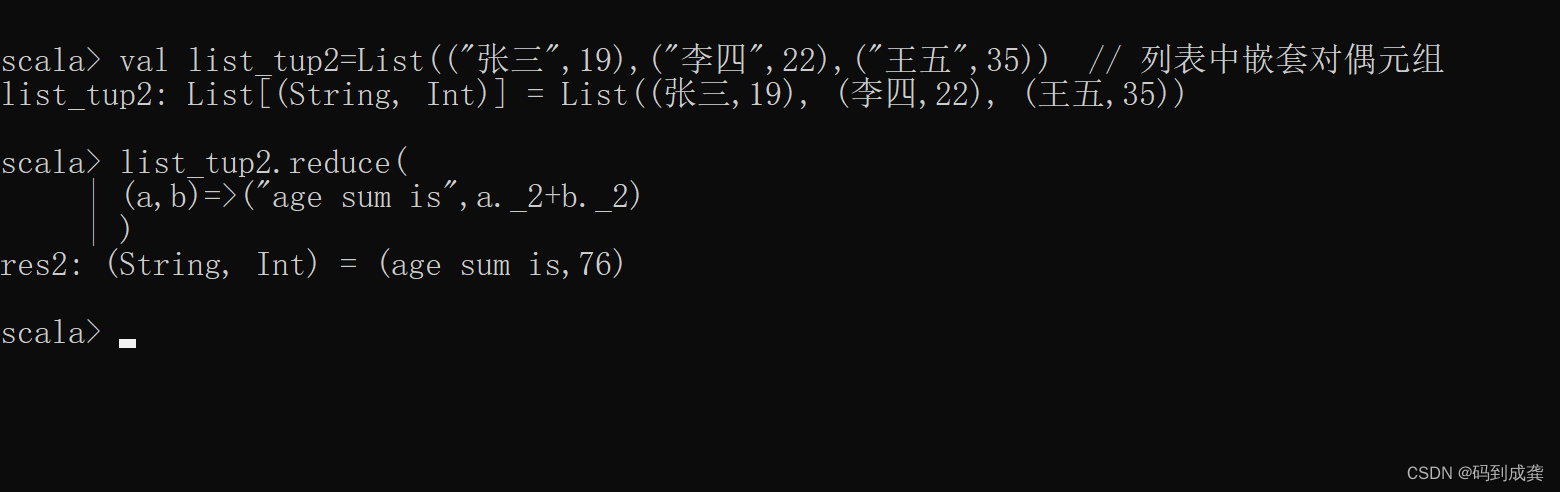
之前我已经能够用非嵌套的集合序列来调用reduce函数，实现一系列的操作，但是如果我们的列表里面嵌套了对偶元组：List(("张三",19),("李四",22),("王五",35))

那么如果想要将对偶元组中的数字都取出来并进行求和运算的话，我该怎么办？这个时候需要注意的是因为原来的集合序列是含有对偶元组的，所以我们在使用reduce函数时，返回值也应该是对偶元组，处理如下：

scala> list_tup2.reduce(   // 对含有对偶元组的列表集合序列进行处理
     | (a,b)=>("age sum is",a._2+b._2)   //  因为含有字符串，所以返回值也得有字符串，与求和后的结果组合成对偶元组
     | )

3，reduceLeft：无嵌套的列表

reduceLeft函数和reduce函数一样，a的取值都是将集合序列最左边的数值作为起始值，并随着使用表达式的结果而变化，b的值依旧是只能从集合序列中从左往右取。例如，现在有一个列表集合序列List(1,2,3,4)，当我们使用reduce函数并将其表达式设置为a+b，那么a的值就会是：1（a的初始值即集合序列中的第一个元素），1+2(a+b，b为集合序列中的第二个元素)，1+2+3（a的值为上一步计算的结果，b的值依旧是从集合序列中以此选取），1+2+3+4。

b的值为：2，3，4。

接下来我使用代码来看一下具体的效果：

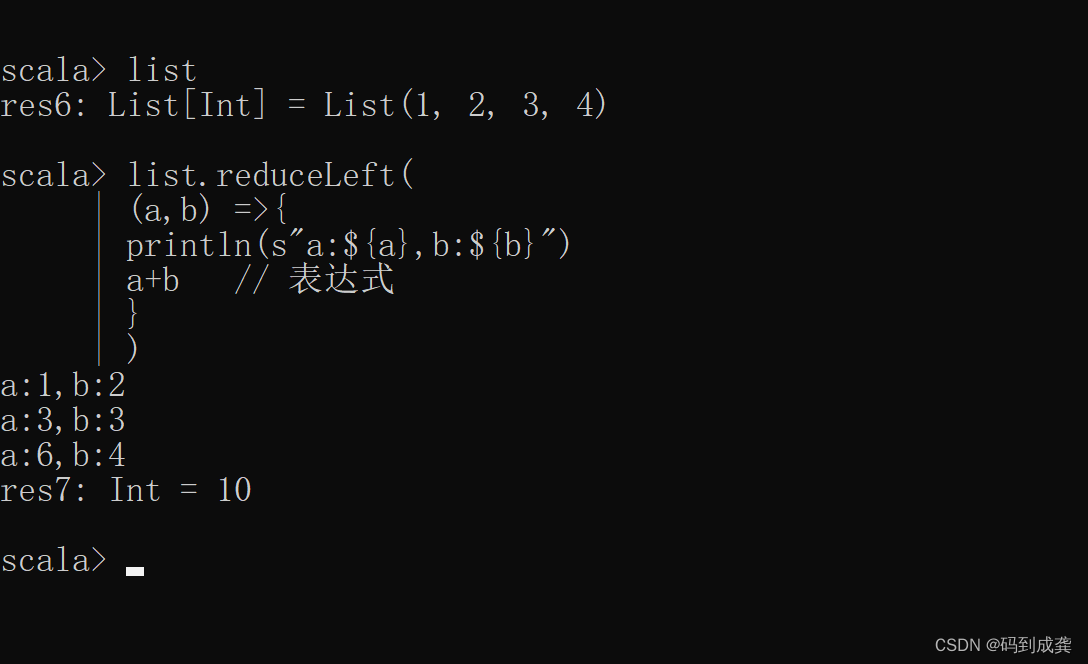
scala> list.reduceLeft(
     | (a,b) =>{
     | println(s"a:${a},b:${b}")  // 打印a和b具体的值
     | a+b   // 表达式
     | }
     | )

如果我使用reduce函数的话，结果都是一样的：

所以，reduce函数和reduceLeft函数的使用看个人喜欢就行。

接下来去认识一个与reduce和reduceLeft函数相反的函数reduceRight函数。

三，reduceRight函数

reduceRight函数与reduce及reduceLeft函数不同，其中b的初始化值是从集合序列的最后一个元素选取即集合序列的最右边的元素为a的第一个值。之后，a的取值就是从集合序列中的倒数第二个开始选取。例如List(1,2,3,4)，如果我们对其使用reduceRight函数，那么b的值就会是：4，4+3，4+3+2，4+3+2+1。a的值会是3，2，1。最后b的值是10。如下：

scala> list.reduceRight(
     | (a,b)=>
     | {
     | println(s"a:${a},b:${b}")
     | a+b}
     | )

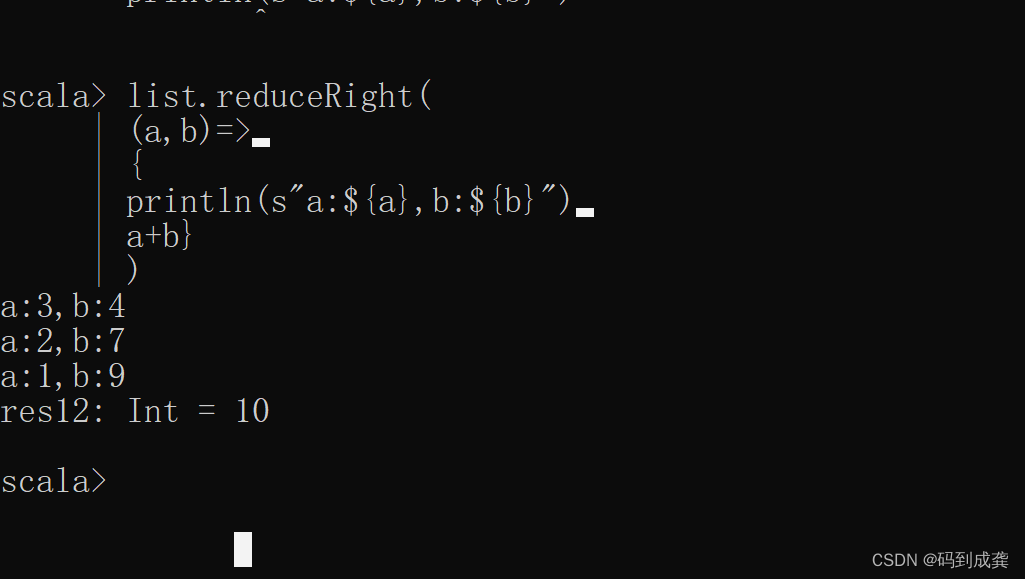
如上，我可以发现现在变成了a的值从集合序列中选取，而b的值是经过表达式之后的结果（b的初始值为集合序列中的最后一个元素）。

四，fold函数及foldLeft函数

fold函数及foldLeft函数和之前的reduce及reduceLeft函数相比，可以给第一个数指定一个积累的初始值。例如集合序列：List（1，2，3，4）使用reduce或redueLeft函数时，a的初始化值一定是集合序列中的第一个元素，但是如果使用了fold或者是foldLeft函数的话，a的初始化值可以不从集合序列中选取，而是可以指定。那么究竟是怎么样的？现在我使用代码来查看相关的结果：

scala> list.fold(10)(  // 指定a的初始化值为10
     | (a,b)=>{
     | println(s"a:${a},b:${b}")
     | a+b
     | }
     | )

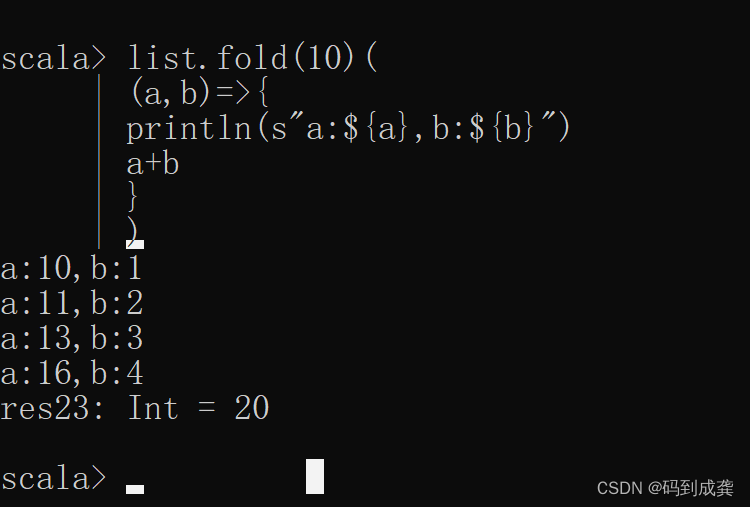
如上，我可以看到，a的值不再是从集合序列中选取，而是fold函数中的第一个参数10，当a不从集合序列中选取初始化值时，b的值就可以从集合序列中的第一个元素开始选取。

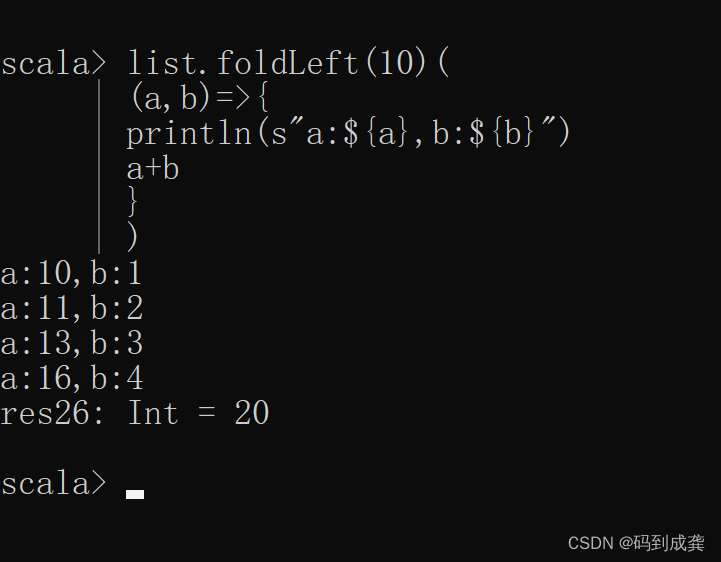
当然，使用foldLeft函数和fold函数实现的效果一样。

scala> list.foldLeft(10)(
     | (a,b)=>{
     | println(s"a:${a},b:${b}")
     | a+b
     | }
     | )

五，foldRight函数

foldRight函数和reduceRight函数的区别在与foldRight函数可以指定b的初始化值，而不是从集合序列中选取。并且b的初始化值就是foldRight函数中的指定的第一个参数值。

现在我使用具体的代码来看看具体的效果：

scala> list.foldRight(10)(
     | (a,b)=>{
     | println(s"a:${a},b:${b}")
     | a+b
     | }
     | )

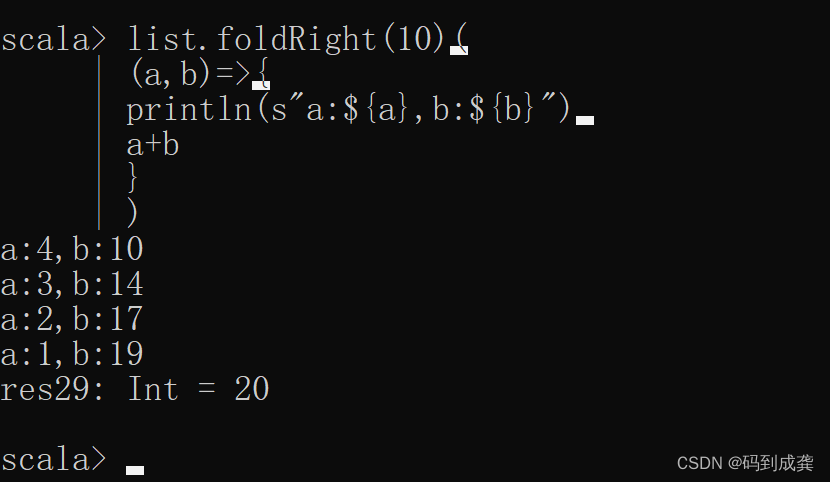
如上，我们可以看到，foldRight中的a和b的运算逻辑其实还是和reduceRight函数一样的，只是b的取值可以指定了而已。

六，aggregate函数及par函数

aggregate函数相比于reduce，reduceLeft函数，aggregate函数可以像fold函数那样传入积累的初始化值，并且也有fold函数没有的功能：可以让传入的参数执行两个表达式，而不仅仅是一个（但是想要两个表达式都执行需要条件）。

相比于fold，foldLeft函数，aggregate函数可以定义两个表达式，第一个表达式为seqOp，第二个表达式为comOp。只有当待处理的集合序列是并行集合，才会去执行comOp表达式。现在我去使用代码来看一下它们的具体效果。

par函数最主要的作用就是将集合序列转换成并行集合。

1，非并行集合使用aggregate函数

现在我们对集合序列List(1,2,3,4)来使用aggregate函数，并定义两个表达式都用于对集合中的元素求和：

scala> list.aggregate(10)(
     | (a,b)=>{
     |  println(s"a:${a},b:${b}")
     | a+b // 全局聚合
     | },
     | (a,b)=>{
     |  println(s"comOp=>a:${a},b:${b}")
     | a+b // 局部聚合
     | })

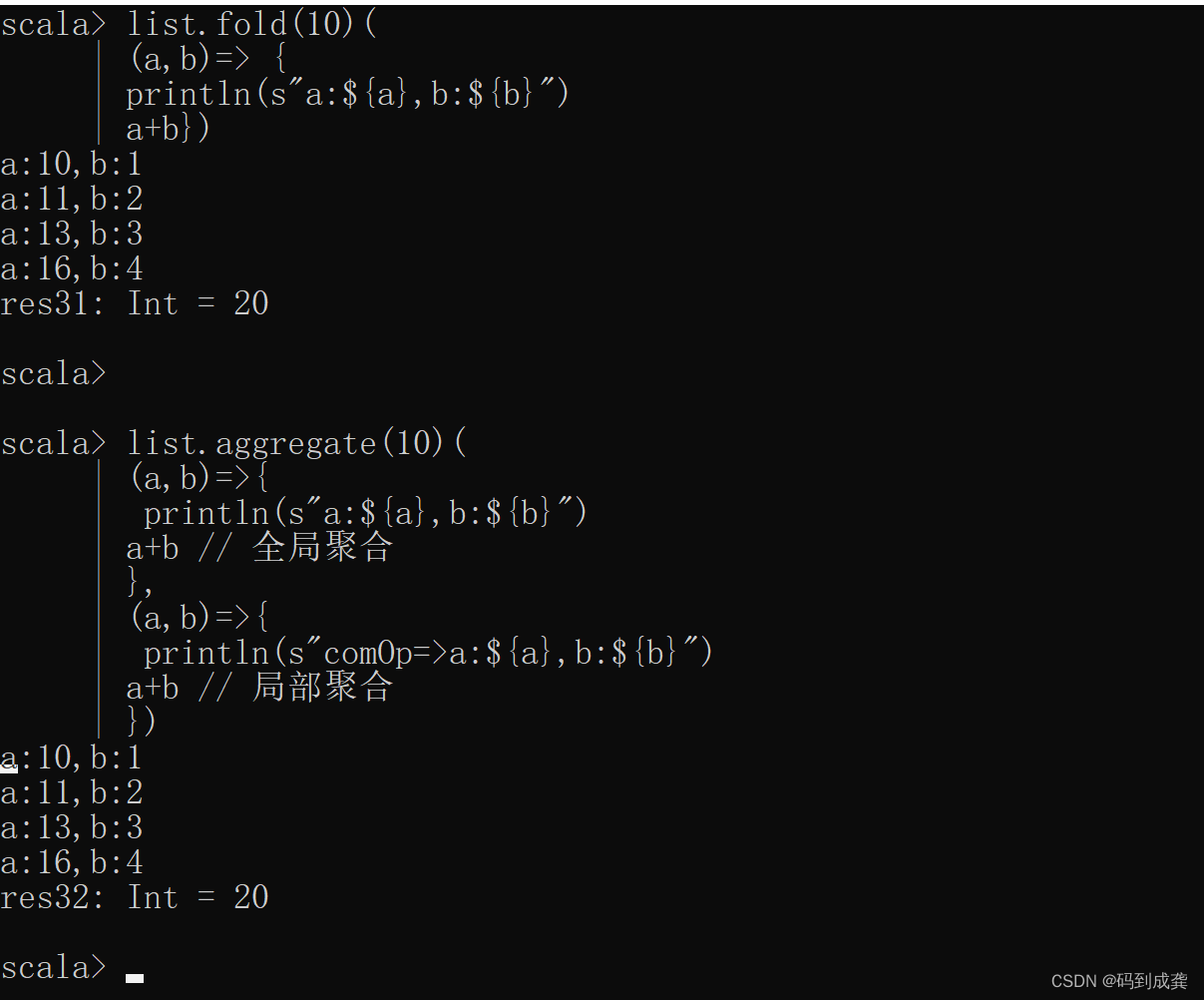
如上，我发现当集合序列不是并行集合时，就不会去执行comOp函数部分的表达式。并且运算的结果和fold（10）的结果一样。

2，并行集合使用aggregate函数

当集合是并行集合时，调用aggregate函数后a的初始化值为aggregate（10）中的10。

并且，因为是并行集合，所以在使用sepOp函数中的表达式a+b时，a的值都是10，b的值从集合序列中选取；在使用comOp函数中的表达式时，a的初始化值为之前全局聚合时第一个分区内元素聚合后的结果，之后的每一次值都为comOp函数局部聚合后的结果。如下为集合List(1,2,3,4)转换成并行集合后调用aggregate函数时在两个聚合函数都使用了相加的过程中a和b的值（仅供参考）：

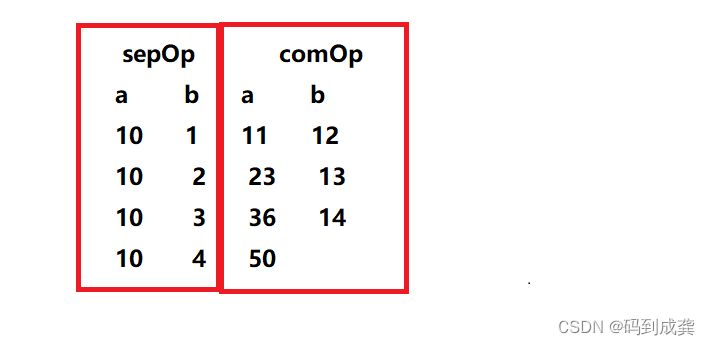
接下来我使用代码来验证这种计算是否正确，如下：

package aggregates
/**
 * @author:码到成龚
 * my motoo:"听闻少年二字，应与平庸相斥。"
 */
object Aggregate {
  def main(args: Array[String]): Unit = {
    val ar_im=Array(1,2,3,4)
    /**
    aggregate有合计的意思。
     *sepOp函数可以将每个分区的元素进行聚合，[全局聚合]
     然后用combine函数将每个分区的结果和初始值进行combine操作【局部聚合】
     （局部聚合加全局聚合）
     aggregate函数的第一个参数可以选择聚合之后的结果
     加上或者是减去的指定数值
     */
    val res=ar_im.par.aggregate(10)(
      (a,b)=>{
        println(s"sepOp => a:${a},b:${b}")
        a+b
      },
      (a,b)=>{
        println(s"comOp => a:${a},b:${b}")
        a+b
      }
    )
    println(res)
  }
}