作者：几冬雪来  

时间：2023年4月14日

内容：数据结构排序内容讲解

目录

前言： 

1.非递归归并排序：

2.越界情况： 

3.计数排序： 

结尾： 

---

前言： 

在上一篇博客中我们对归并排序非递归形式做了一个大致的讲解，并且搭构了它的大概框架，但是我们非递归形式的归并排序有许多的陷阱在，而今天我们就要将其进行完善。

1.非递归归并排序：

在上一篇博客中我们大概的搭建了非递归归并排序的大概框架，现在我们将代码再次放出来并对它进行一个运行。

  

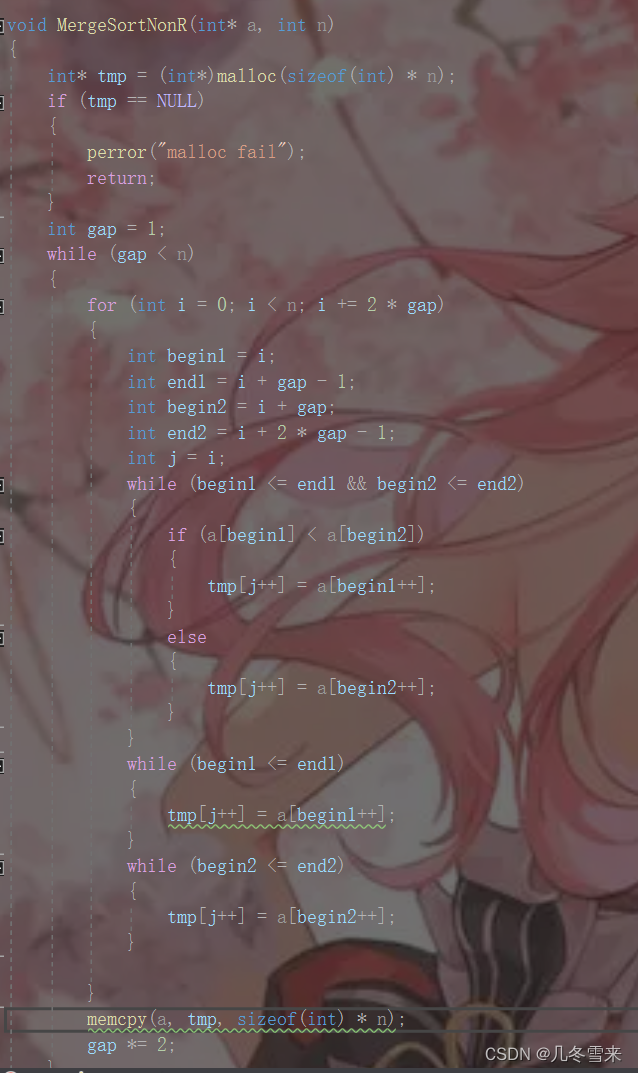
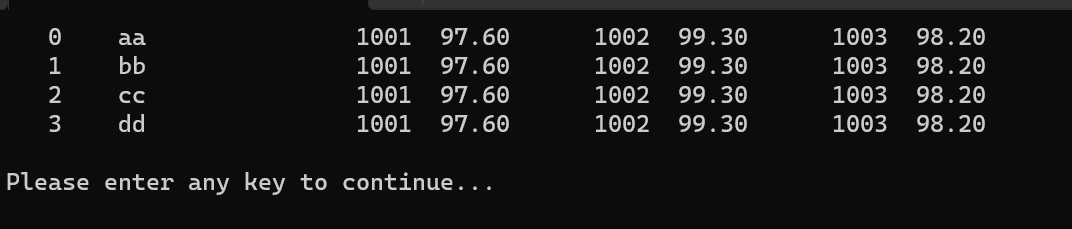
在这里我们输入的依旧是8个数，然后我们来看看运行的结果是什么？ 

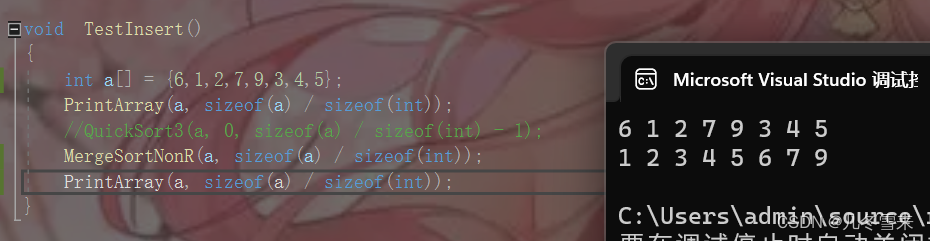
从这里我们可以看出来在8个数的时候，我们的归并排序非递归形式成功的帮助我们进行排序了，但是如果在这里我们数组的大小不为2的n次方的时候，这个时候会发生什么事情呢？我们将数组的个数上升到9个来试试看。 

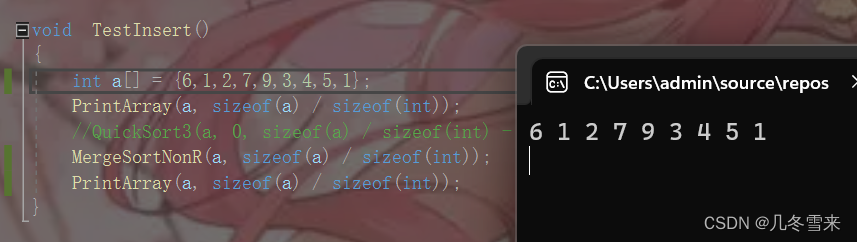
如果换为9个数的数组，从结果上来看我们的程序很明显的崩溃了，最主要的原因就是我们的gap每次都乘等于2，导致最后发生了越界。 

2.越界情况： 

前面提到了程序崩溃是因为越界的情况。而在归并排序中，我们将我们的原数组给拆分为了两个行的数组，因此这里我们要对4个边界进行判断。

接下来我们就来对我们的代码分类并进行修正。 

这就是我们修正的代码，可能会有人看不懂我们这里在干什么，没关系我们可以画一个图来对它进行一个具体的表示。 

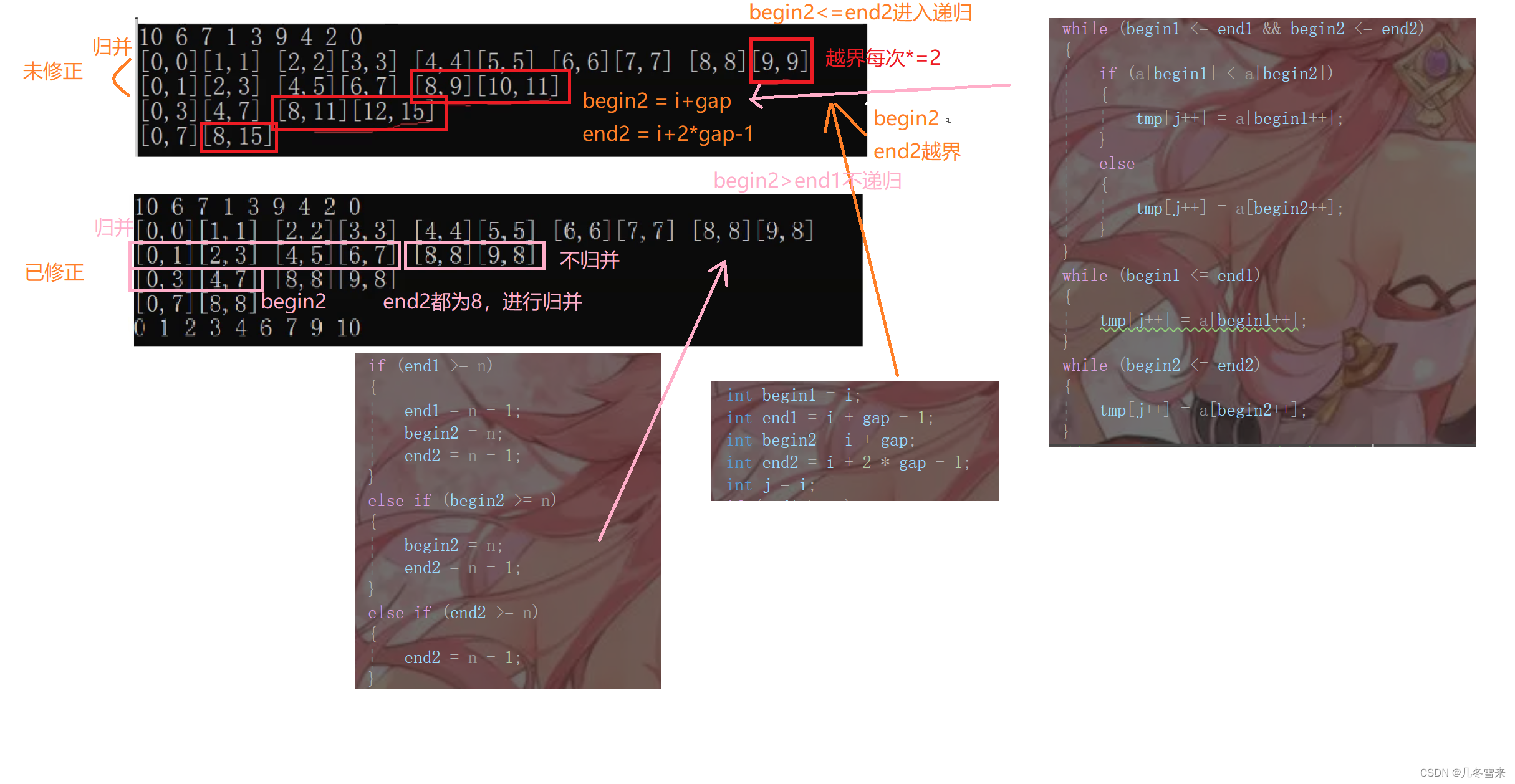
这就是我们代码修正过后的操作。这里我们的拷贝函数的代码是在for循环语句外进行的，同样的我们还有一种方法是让拷贝代码的函数在for循环语句内进行的，前者是整个还是都归并完毕再一次性的拷贝回原函数，后者是执行一次归并结束后就拷贝一次。

而如果我们要使用这种方法的话，代码也要进行一定程度的修改。

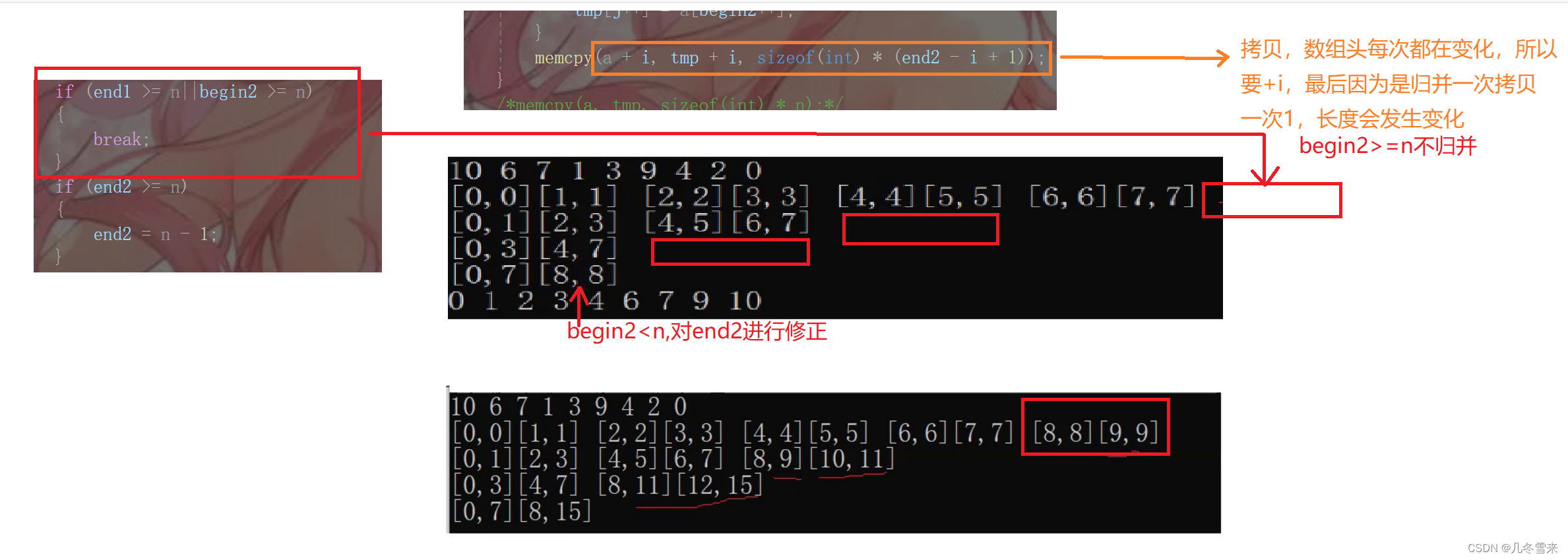
在这里就是我们另外一种的拷贝方式，因为是部分拷贝的方法，所以在这里如果end1和begin2满足条件会跳过也是可以的，我们第一种方法是需要一次性都拷贝下来的所以在这里我们不能跳过。 

这里就是我们递归排序非递归形式的修改，主要修改的就是它的越界的问题。 

3.计数排序： 

在接下来讲解的是我们的一种非比较排序法——计数排序。 

那么在这里我们的计算排序是怎么操作的呢，我们在这里给一个数组。

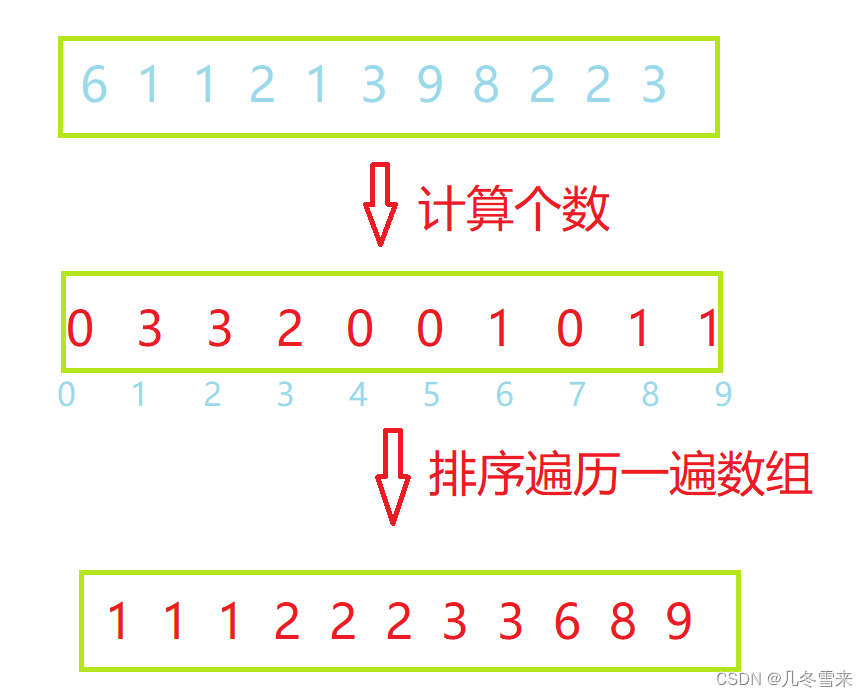
这就是我们的计算排序，它的原理就是选一个数组计算我们的每个元素的个数，最后再遍历和排序我们的数组就行了，这就是我们的计数排序，准确的应该叫——绝对位置映射计算。 

但是这种代码也存在着它的问题，如果这里我们数组中元素的大小都是100,102等的数，如果我们依旧从1开始开辟空间的话，前面我们1-99的空间就浪费掉了。 

所以这里我们就用另外一种方法，在这里我们用a[i] - min来计算，也就是将其放在1的位置。但是这种方法也只是解我们的一时之需罢了，而这种方法被我们叫做——相对位置映射计算。

总结来说就是我们的这种方法适合：计数排序范围集中且个数不多的整形排序。并且在某些特殊场合中，它运行的十分之快。

接下来就是来书写我们的代码。

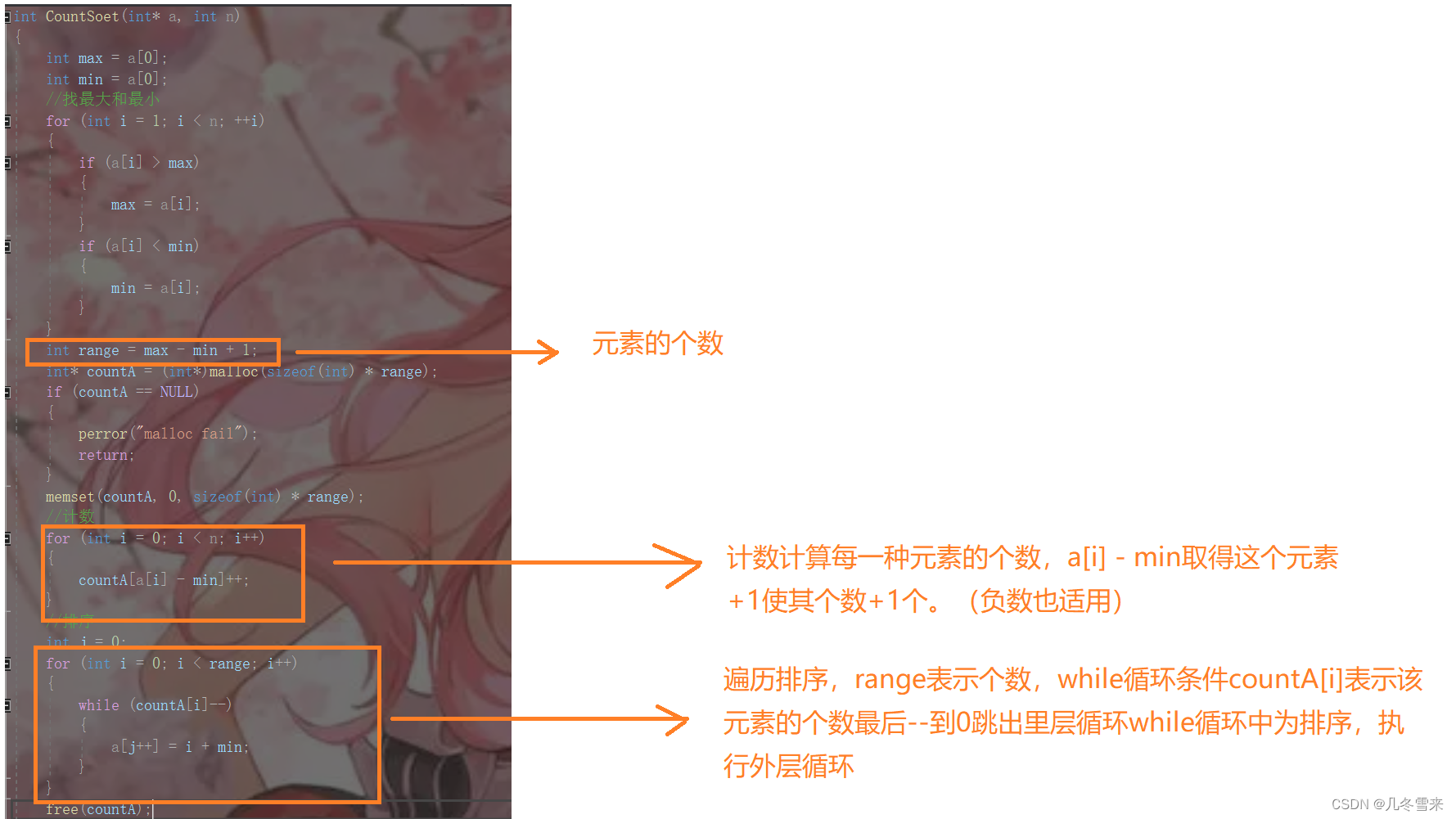
这里就是我们的计数排序的代码，但是在现实中我们的计数排序并没有被广泛的使用到，因为它的局限太多，哪怕在某种特殊情况下它的时间复杂度可以很快，但是这里却是消耗了它的空间复杂度。 

结尾： 

到这里，我们数据结构所有的排序就都学习过了，这个板块也即将完结。在上一篇博客中我们将对数据结构的排序板块的知识做一个总结，同时我们的数据结构的课程也要临近结束了。最后希望这篇博客能为大家提供帮助。