DFIG控制10: 双馈发电机的动态模型。主要介绍DFIG在三相坐标系、定子αβ坐标系、dq同步坐标系下的模型。
本文主要是整理了DFIG的动态模型的公式和坐标变换的过程。某些描述是为了便于自己理解,不一定准确。
大部分内容参考:
G. Abad, J. Lopez, M. Rodriguez, L. Marroyo, and G. Iwanski, Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation. John Wiley & Sons, 2011.
模型主要包括4个方程:电压、磁链、转矩、运动。
三相坐标系模型
示意图
示意图如下,ABC定子,里面的转子abc在旋转。转子的各个参数已经折算到定子侧,折算后定子和转子的匝数相同。(折算方式类似于变压器的原副边折算)。转子的三个绕组旋转的角速度为转子的电角速度 θ r \theta_r θr,是机械角速度乘以极对数 n p θ m n_p\theta_m npθm
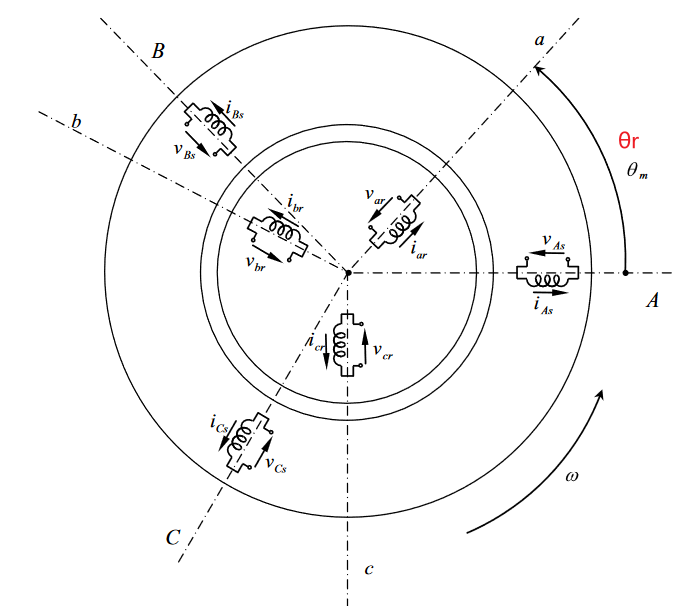
电压方程
对于定子:
u
A
,
B
,
C
=
R
s
i
A
,
B
,
C
+
d
ψ
A
,
B
,
C
d
t
u_{A,B,C}=R_si_{A,B,C}+\frac{d\psi_{A,B,C}}{dt}
uA,B,C=RsiA,B,C+dtdψA,B,C
其实就是电压和磁链的关系(电磁感应定律),并且考虑了绕组内阻上的压降 。
或者写成矩阵形式:
[
u
A
u
B
u
C
]
=
[
R
s
0
0
0
R
s
0
0
0
R
s
]
[
i
A
i
B
i
C
]
+
d
d
t
[
ψ
A
ψ
B
ψ
C
]
\left[\begin{matrix} u_A \\ u_B \\ u_C \end{matrix}\right] = \left[\begin{matrix} R_s & 0 & 0 \\ 0 & R_s & 0 \\ 0 & 0 & R_s \end{matrix}\right] \left[\begin{matrix} i_A \\ i_B \\ i_C \end{matrix}\right] + \frac{d}{dt}\left[\begin{matrix} \psi_A \\ \psi_B \\ \psi_C \end{matrix}\right]
uAuBuC
=
Rs000Rs000Rs
iAiBiC
+dtd
ψAψBψC
R
s
R_s
Rs为定子绕组的内阻。
对于转子,
u
a
,
b
,
c
=
R
r
i
a
,
b
,
c
+
d
ψ
a
,
b
,
c
d
t
u_{a,b,c}=R_ri_{a,b,c}+\frac{d\psi_{a,b,c}}{dt}
ua,b,c=Rria,b,c+dtdψa,b,c
R
s
R_s
Rs为转子绕组的内阻。
或者写成矩阵形式:
[
u
a
u
b
u
c
]
=
[
R
r
0
0
0
R
r
0
0
0
R
r
]
[
i
a
i
c
i
c
]
+
d
d
t
[
ψ
a
ψ
b
ψ
c
]
\left[\begin{matrix} u_a \\ u_b \\ u_c \end{matrix}\right] = \left[\begin{matrix} R_r & 0 & 0 \\ 0 & R_r & 0 \\ 0 & 0 & R_r \end{matrix}\right] \left[\begin{matrix} i_a \\ i_c \\ i_c \end{matrix}\right] + \frac{d}{dt}\left[\begin{matrix} \psi_a \\ \psi_b \\ \psi_c \end{matrix}\right]
uaubuc
=
Rr000Rr000Rr
iaicic
+dtd
ψaψbψc
磁链方程
这部分内容还是可以参考变压器的模型。看了这个视频,觉得讲得还挺清楚的:第十一讲 风力发电系统基本结构+双馈电机数学模型第一部分_哔哩哔哩_bilibili
把DFIG的3个定子绕组相当于3个位置固定的电感(星形连接的),而3个转子绕组相当于3个旋转的电感(也是星形连接的)。这些电感的部分磁链于其他电感有交链,也有部分只在绕组自身交链(类似变压器的漏感)。
考虑所有这些交链关系(
ψ
=
∑
L
x
i
x
\psi=\sum L_xi_x
ψ=∑Lxix),定子和转子的磁链为:
[
ψ
A
ψ
B
ψ
C
ψ
a
ψ
b
ψ
c
]
=
[
L
A
A
L
A
B
L
A
C
L
A
a
L
A
b
L
A
c
L
B
A
L
B
B
L
B
C
L
B
a
L
B
b
L
B
c
L
C
A
L
C
B
L
C
C
L
C
a
L
C
b
L
C
c
L
a
A
L
a
B
L
a
C
L
a
a
L
a
b
L
a
c
L
b
A
L
b
B
L
b
C
L
b
a
L
b
b
L
b
c
L
c
A
L
c
B
L
c
C
L
c
a
L
c
b
L
c
c
]
[
i
A
i
B
i
C
i
a
i
b
i
c
]
\left[\begin{matrix} \psi_A \\ \psi_B \\ \psi_C \\ \psi_a \\ \psi_b \\ \psi_c \end{matrix}\right] = \left[\begin{matrix} L_{AA} & L_{AB} & L_{AC} & L_{Aa} & L_{Ab} & L_{Ac}\\ L_{BA} & L_{BB} & L_{BC} & L_{Ba} & L_{Bb} & L_{Bc} \\ L_{CA} & L_{CB} & L_{CC} & L_{Ca} & L_{Cb} & L_{Cc} \\ L_{aA} & L_{aB} & L_{aC} & L_{aa} & L_{ab} & L_{ac}\\ L_{bA} & L_{bB} & L_{bC} & L_{ba} & L_{bb} & L_{bc} \\ L_{cA} & L_{cB} & L_{cC} & L_{ca} & L_{cb} & L_{cc} \\ \end{matrix}\right] \left[\begin{matrix} i_A \\ i_B \\ i_C \\ i_a \\ i_b \\ i_c \end{matrix}\right]
ψAψBψCψaψbψc
=
LAALBALCALaALbALcALABLBBLCBLaBLbBLcBLACLBCLCCLaCLbCLcCLAaLBaLCaLaaLbaLcaLAbLBbLCbLabLbbLcbLAcLBcLCcLacLbcLcc
iAiBiCiaibic
其中,定子-定子之间以及转子-转子之间的电感,由于相对位置是固定的,所以电感值是常数。而定子-转子之间的电感,由于转子在转动,电感值随转子的电角度
θ
r
\theta_r
θr变化。
所以可以分成4部分:
[
ψ
s
ψ
r
]
=
[
L
s
s
L
s
r
(
θ
r
)
L
r
s
(
θ
r
)
L
r
r
]
[
i
s
i
r
]
\left[\begin{matrix} \boldsymbol{\psi}_s \\ \boldsymbol{\psi}_r \end{matrix}\right] = \left[\begin{matrix} \boldsymbol{L}_{ss} & \boldsymbol{L}_{sr}(\theta_r) \\ \boldsymbol{L}_{rs}(\theta_r) & \boldsymbol{L}_{rr} \end{matrix}\right] \left[\begin{matrix} \boldsymbol{i}_s \\ \boldsymbol{i}_r \end{matrix}\right]
[ψsψr]=[LssLrs(θr)Lsr(θr)Lrr][isir]
下标s表示定子的3个变量,下标r表示转子的3个变量。6x6的电感矩阵,按照系数是否随电角度变化,分成了4个3x3的矩阵。
再来看一下这4个矩阵。
定子:
L
s
s
=
[
L
m
+
L
l
s
−
0.5
L
m
−
0.5
L
m
−
0.5
L
m
L
m
+
L
l
s
−
0.5
L
m
−
0.5
L
m
−
0.5
L
m
L
m
+
L
l
s
]
\boldsymbol{L}_{ss}= \left[\begin{matrix} L_{m}+L_{ls} & -0.5L_m & -0.5L_m \\ -0.5L_m & L_{m}+L_{ls} & -0.5L_m \\ -0.5L_m & -0.5L_m & L_{m}+L_{ls} \end{matrix}\right]
Lss=
Lm+Lls−0.5Lm−0.5Lm−0.5LmLm+Lls−0.5Lm−0.5Lm−0.5LmLm+Lls
L
m
L_m
Lm是磁链有交链的部分,由于三相绕组120°的位置关系,其他两相绕组对另一相的互感都是
L
m
c
o
s
12
0
∘
=
−
0.5
L
m
L_m cos120^\circ=-0.5L_m
Lmcos120∘=−0.5Lm,没有交链的是定子每相的漏感
L
l
s
L_{ls}
Lls。
转子侧公式类似:
L
r
r
=
[
L
m
+
L
l
r
−
0.5
L
m
−
0.5
L
m
−
0.5
L
m
L
m
+
L
l
r
−
0.5
L
m
−
0.5
L
m
−
0.5
L
m
L
m
+
L
l
r
]
\boldsymbol{L}_{rr}= \left[\begin{matrix} L_{m}+L_{lr} & -0.5L_m & -0.5L_m \\ -0.5L_m & L_{m}+L_{lr} & -0.5L_m \\ -0.5L_m & -0.5L_m & L_{m}+L_{lr} \end{matrix}\right]
Lrr=
Lm+Llr−0.5Lm−0.5Lm−0.5LmLm+Llr−0.5Lm−0.5Lm−0.5LmLm+Llr
注意因为做了折算,交链的部分和定子一样,为
L
m
L_m
Lm。不同的是,转子每相的漏感为
L
l
r
L_{lr}
Llr。
定子转子之间:
L
s
r
(
θ
r
)
=
L
r
s
(
θ
r
)
T
=
[
L
A
a
L
A
b
L
A
c
L
B
a
L
B
b
L
B
c
L
C
a
L
C
b
L
C
c
]
=
L
m
[
c
o
s
(
θ
r
)
c
o
s
(
θ
r
+
12
0
∘
)
c
o
s
(
θ
r
−
12
0
∘
)
c
o
s
(
θ
r
−
12
0
∘
)
c
o
s
(
θ
r
)
c
o
s
(
θ
r
+
12
0
∘
)
c
o
s
(
θ
r
+
12
0
∘
)
c
o
s
(
θ
r
−
12
0
∘
)
c
o
s
(
θ
r
)
]
\begin{align*} &\boldsymbol{L}_{sr}(\theta_r)=\boldsymbol{L}_{rs}(\theta_r)^T = \left[\begin{matrix} L_{Aa} & L_{Ab} & L_{Ac}\\ L_{Ba} & L_{Bb} & L_{Bc} \\ L_{Ca} & L_{Cb} & L_{Cc} \\ \end{matrix}\right]\\ &=L_m\left[\begin{matrix} cos(\theta_r) & cos(\theta_r+120^\circ) & cos(\theta_r-120^\circ) \\ cos(\theta_r-120^\circ) & cos(\theta_r) & cos(\theta_r+120^\circ) \\ cos(\theta_r+120^\circ) & cos(\theta_r-120^\circ) & cos(\theta_r) \end{matrix}\right]\end{align*}
Lsr(θr)=Lrs(θr)T=
LAaLBaLCaLAbLBbLCbLAcLBcLCc
=Lm
cos(θr)cos(θr−120∘)cos(θr+120∘)cos(θr+120∘)cos(θr)cos(θr−120∘)cos(θr−120∘)cos(θr+120∘)cos(θr)
看第一行:当转子的a相和定子的A相重合时,
θ
r
=
0
\theta_r=0
θr=0,此时互感
L
A
a
L_{Aa}
LAa达到最大值
L
m
L_m
Lm。此时转子b相的物理位置超前a相120°,c相超前240°(相当于滞后120°),所以有这样的表达式。先了解到这里,没继续看更细节的内容。(这里简单认为极对数=1)
转矩和运动方程
这个没仔细看,只记录一下公式,后面转矩方程需要和电压、磁链方程一起做坐标变换。(发现篇幅太长了,转矩部分还是下次再写)。
转矩方程:
T
e
=
n
p
L
m
[
(
i
A
i
a
+
i
B
i
b
+
i
C
i
c
)
s
i
n
θ
r
+
(
i
A
i
b
+
i
B
i
c
+
i
C
i
a
)
s
i
n
(
θ
r
+
12
0
∘
)
+
(
i
A
i
c
+
i
B
i
a
+
i
C
i
b
)
s
i
n
(
θ
r
−
12
0
∘
)
]
\begin{align*} T_e=& n_pL_m[(i_Ai_a+i_Bi_b+i_Ci_c)sin\theta_r+\\ & (i_Ai_b+i_Bi_c+i_Ci_a)sin(\theta_r+120^\circ)+ \\ & (i_Ai_c+i_Bi_a+i_Ci_b )sin(\theta_r-120^\circ)] \end{align*}
Te=npLm[(iAia+iBib+iCic)sinθr+(iAib+iBic+iCia)sin(θr+120∘)+(iAic+iBia+iCib)sin(θr−120∘)]
理想的运动方程(应该是大物里面见过):
J
n
p
d
ω
r
d
t
=
T
e
−
T
L
\frac{J}{n_p}\frac{d\omega_r}{dt}=T_e-T_L
npJdtdωr=Te−TL
描述了电机在电磁转矩
T
e
T_e
Te和负载转矩
T
L
T_L
TL作用下的加减速。
ω
r
/
n
p
\omega_r/n_p
ωr/np为机械角速度,J为转动惯量。
定子αβ静止坐标系模型
为了简化模型,引入了3/2变换(Clarke变换)。主要是基于三相电压、电流有一定关系,不是完全独立的:比如在星形连接中, i a + i b + i c = 0 i_a+i_b+i_c=0 ia+ib+ic=0,所以知道两相的值就可以求得另一相的值;三相电流实际只需要两个量来表示。(具体原理可以参考其他文章,比如,手撕系列(2):Clark变换与Park变换 - 知乎 (zhihu.com))
这里强调定子αβ静止坐标系,是因为转子的变量经过3/2变换后,是在
相对转子静止的转子αβ坐标系上,而这个坐标系(后面按照参考书的方式称为转子DQ坐标系)相对定子αβ静止坐标系以转子的电角速度 ω r \omega_r ωr旋转
abc三相坐标系、定子αβ静止坐标系、转子DQ坐标系、同步dq坐标系的关系:
- abc三相坐标系没画全,a轴和α轴重合。
- 转子DQ坐标系和同步dq坐标系都是在旋转的,角速度如下。
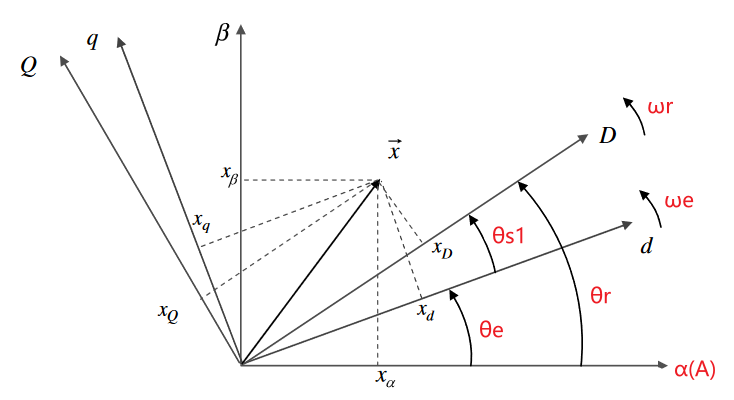
这里使用等幅值变换,并且A轴和α轴重合:
[
x
α
x
β
x
0
]
=
T
3
/
2
[
x
a
x
b
x
c
]
=
2
3
[
1
−
1
2
−
1
2
0
3
2
−
3
2
1
2
1
2
1
2
]
[
x
a
x
b
x
c
]
\left[ \begin{matrix} x_\alpha \\ x_\beta \\ x_0 \end{matrix} \right] =T_{3/2}\left[ \begin{matrix} x_a \\ x_b \\ x_c \end{matrix} \right]= \frac{2}{3} \left[ \begin{matrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix} \right] \left[ \begin{matrix} x_a \\ x_b \\ x_c \end{matrix} \right]
xαxβx0
=T3/2
xaxbxc
=32
1021−212321−21−2321
xaxbxc
变换矩阵把第三行也加上,只是为了后面便于计算逆矩阵。
使用矢量表示
一些推导在矢量表示下更方便。
举例如下:
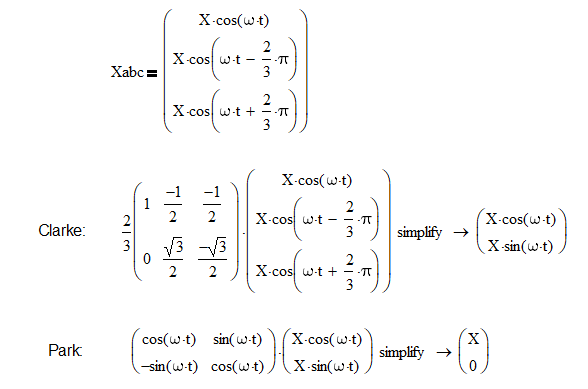
[
X
c
o
s
(
ω
t
)
X
c
o
s
(
ω
t
−
2
3
π
)
X
c
o
s
(
ω
t
+
2
3
π
)
]
→
T
3
/
2
[
X
c
o
s
(
ω
t
)
X
s
i
n
(
ω
t
)
]
→
T
α
β
/
d
q
[
X
0
]
\left[ \begin{matrix} Xcos(\omega t) \\ Xcos(\omega t-\frac{2}{3}\pi) \\Xcos(\omega t+\frac{2}{3}\pi) \end{matrix} \right] \xrightarrow{T_{3/2}} \left[ \begin{matrix} Xcos(\omega t) \\ Xsin(\omega t) \end{matrix} \right] \xrightarrow{T_{\alpha\beta/dq}} \left[ \begin{matrix} X \\ 0 \end{matrix} \right]
Xcos(ωt)Xcos(ωt−32π)Xcos(ωt+32π)
T3/2[Xcos(ωt)Xsin(ωt)]Tαβ/dq[X0]
这个过程也可以用矢量表示为:
[
X
c
o
s
(
ω
t
)
X
c
o
s
(
ω
t
−
2
3
π
)
X
c
o
s
(
ω
t
+
2
3
π
)
]
→
T
3
/
2
X
⃗
α
β
=
X
c
o
s
(
ω
t
)
+
j
X
s
i
n
(
ω
t
)
=
X
e
j
ω
t
→
e
−
j
ω
t
X
⃗
d
q
=
X
\begin{align*} \left[ \begin{matrix} Xcos(\omega t) \\ Xcos(\omega t-\frac{2}{3}\pi) \\Xcos(\omega t+\frac{2}{3}\pi) \end{matrix} \right] \xrightarrow{T_{3/2}} & \vec{X}^{\alpha\beta}=Xcos(\omega t) + jXsin(\omega t)=Xe^{j\omega t} \\ \xrightarrow{e^{-j\omega t}} & \vec{X}^{dq}=X \end{align*}
Xcos(ωt)Xcos(ωt−32π)Xcos(ωt+32π)
T3/2e−jωtXαβ=Xcos(ωt)+jXsin(ωt)=XejωtXdq=X
- 经过Clarke变换后,把α轴分量作为实部,β轴分量作为虚部,平衡的三相信号可以表示为一个在αβ坐标系逆时针旋转的矢量,矢量的模等于X(因为等幅值变换),角速度为 ω \omega ω,角度为 ω t \omega t ωt。
- 如果采用dq同步坐标系,就是说让坐标系与信号同步旋转,在dq坐标系下,三相信号最终变成了一个静止的矢量。
- 注意αβ->dq变换(Park变换)是对信号做运算,其目的是把信号变换到一个
逆时针旋转,角速度也为 ω \omega ω的dq坐标系上。而对于信号而言,让坐标轴逆时针旋转,其实就是让信号顺时针旋转,从而抵消在静止坐标系下的角速度,最终得到直流量。这也就是park变换被表示为 e − j ω t e^{-j\omega t} e−jωt的原因。(因为需要用到,把park变换也简单介绍一下)
电压方程(矢量形式)
对定子电压做3/2变换:
[
u
α
u
β
u
0
]
=
T
3
/
2
[
u
A
u
B
u
C
]
=
T
3
/
2
[
R
s
0
0
0
R
s
0
0
0
R
s
]
T
3
/
2
−
1
⋅
T
3
/
2
[
i
A
i
B
i
C
]
+
T
3
/
2
d
d
t
[
ψ
A
ψ
B
ψ
C
]
=
[
R
s
0
0
0
R
s
0
0
0
R
s
]
[
i
α
i
β
i
0
]
+
d
d
t
[
ψ
α
ψ
β
ψ
0
]
\begin{align*} \left[ \begin{matrix} u_\alpha \\ u_\beta \\u_0 \end{matrix} \right] = T_{3/2}\left[\begin{matrix} u_A \\ u_B \\ u_C \end{matrix}\right] &= T_{3/2} \left[\begin{matrix} R_s & 0 & 0 \\ 0 & R_s & 0 \\ 0 & 0 & R_s \end{matrix}\right] T_{3/2}^{-1}\cdot T_{3/2} \left[\begin{matrix} i_A \\ i_B \\ i_C \end{matrix}\right] + T_{3/2} \frac{d}{dt}\left[\begin{matrix} \psi_A \\ \psi_B \\ \psi_C \end{matrix}\right] \\ &=\left[\begin{matrix} R_s & 0 & 0 \\ 0 & R_s & 0 \\ 0 & 0 & R_s \end{matrix}\right]\left[ \begin{matrix} i_\alpha \\ i_\beta \\ i_0 \end{matrix} \right] + \frac{d}{dt}\left[\begin{matrix} \psi_\alpha \\ \psi_\beta \\ \psi_0 \end{matrix}\right] \end{align*}
uαuβu0
=T3/2
uAuBuC
=T3/2
Rs000Rs000Rs
T3/2−1⋅T3/2
iAiBiC
+T3/2dtd
ψAψBψC
=
Rs000Rs000Rs
iαiβi0
+dtd
ψαψβψ0
注意矩阵中间的
T
3
/
2
−
1
⋅
T
3
/
2
=
E
T_{3/2}^{-1}\cdot T_{3/2}=E
T3/2−1⋅T3/2=E,(单位矩阵)。计算时,
T
3
/
2
−
1
T_{3/2}^{-1}
T3/2−1和前面结合,
T
3
/
2
T_{3/2}
T3/2和后面的电流向量结合,实现αβ转换。
只看前两行,写成矢量形式:
u
⃗
s
=
R
s
i
⃗
s
+
d
d
t
ψ
⃗
s
\vec{u}_s=R_s\vec{i}_s+\frac{d}{dt}\vec{\psi}_s
us=Rsis+dtdψs
从这个方程可以看出,定子电压
u
⃗
s
\vec{u}_s
us的相位超前定子磁链
ψ
⃗
s
\vec{\psi}_s
ψs 约90°(如果忽略
R
s
R_s
Rs)
转子电压和定子电压表达式类似,做3/2变换,省略中间过程,写成矢量形式:
u
⃗
r
r
=
R
r
i
⃗
r
r
+
d
d
t
ψ
⃗
r
r
\vec{u}_r^r=R_r\vec{i}_r^r+\frac{d}{dt}\vec{\psi}_r^r
urr=Rrirr+dtdψrr
注意转子物理量的上标r。此时转子坐标系与定子坐标系不同。
只经过3/2变换,转子的物理量位于相对转子静止的坐标系上(参考书中称为大写的DQ坐标系),而这个坐标系以转子的电角速度
ω
r
\omega_r
ωr旋转,与定子坐标系的夹角为
ω
r
t
\omega_rt
ωrt。
目标是把转子的物理量也放到定子αβ静止坐标系中。所以,需要把转子的坐标系旋转
−
ω
r
t
-\omega_rt
−ωrt,相对地,也就是把转子的物理量旋转
ω
r
t
\omega_rt
ωrt。(有点绕)。这样处理以后,把上标r去掉,表示定子和转子的物理量是在同一个坐标系中(定子αβ静止坐标系):
u
⃗
r
=
u
⃗
r
r
e
j
ω
r
t
=
R
r
i
⃗
r
r
e
j
ω
r
t
+
e
j
ω
r
t
d
d
t
ψ
⃗
r
r
=
R
r
i
⃗
r
+
d
d
t
ψ
⃗
r
−
j
ω
r
ψ
⃗
r
\begin{align*} \vec{u}_r=\vec{u}_r^re^{j\omega_r t} &=R_r\vec{i}_r^re^{j\omega_r t}+e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r \\ &=R_r\vec{i}_r+\frac{d}{dt}\vec{\psi}_r-j\omega_r\vec{\psi}_r \end{align*}
ur=urrejωrt=Rrirrejωrt+ejωrtdtdψrr=Rrir+dtdψr−jωrψr
备注:
1.推导过程其实是复合函数的求导
ψ
⃗
r
=
e
j
ω
r
t
ψ
⃗
r
r
,
d
d
t
ψ
⃗
r
=
d
e
j
ω
r
t
ψ
⃗
r
r
d
t
=
e
j
ω
r
t
d
d
t
ψ
⃗
r
r
+
ψ
⃗
r
r
d
e
j
ω
r
t
d
t
=
e
j
ω
r
t
d
d
t
ψ
⃗
r
r
+
ψ
⃗
r
r
(
j
ω
r
e
j
ω
r
t
)
=
e
j
ω
r
t
d
d
t
ψ
⃗
r
r
+
j
ω
r
ψ
⃗
r
→
e
j
ω
r
t
d
d
t
ψ
⃗
r
r
=
d
d
t
ψ
⃗
r
−
j
ω
r
ψ
⃗
r
\begin{align*} \vec{\psi}_r&=e^{j\omega_r t}\vec{\psi}_r^r, \\ \frac{d}{dt}\vec{\psi}_r &=\frac{de^{j\omega_r t}\vec{\psi}_r^r}{dt} =e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r+\vec{\psi}_r^r\frac{de^{j\omega_r t}}{dt} \\ &=e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r+\vec{\psi}_r^r (j\omega_r e^{j\omega_r t}) \\ &= e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r + j\omega_r\vec{\psi}_r \\ \rightarrow &e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r =\frac{d}{dt}\vec{\psi}_r-j\omega_r\vec{\psi}_r \end{align*}
ψrdtdψr→=ejωrtψrr,=dtdejωrtψrr=ejωrtdtdψrr+ψrrdtdejωrt=ejωrtdtdψrr+ψrr(jωrejωrt)=ejωrtdtdψrr+jωrψrejωrtdtdψrr=dtdψr−jωrψr
2.
−
j
ω
r
ψ
⃗
r
-j\omega_r\vec{\psi}_r
−jωrψr导致转子物理量的αβ分量之间存在耦合
3.转子物理量的角频率为
ω
s
1
=
ω
e
−
ω
r
\omega_{s1}=\omega_e-\omega_r
ωs1=ωe−ωr。(例如,转子电流的角速度=转差角速度=定子(电网)角速度-转子电角速度)。在转子的DQ坐标系中,转子的物理量可以表示为
X
e
j
ω
s
1
t
Xe^{j\omega_{s1}t}
Xejωs1t。转换到定子αβ静止坐标系,转子的物理量变为
X
e
j
ω
s
1
t
e
j
ω
r
t
=
X
e
j
ω
e
t
Xe^{j\omega_{s1}t}e^{j\omega_r t}=Xe^{j\omega_{e}t}
Xejωs1tejωrt=Xejωet。也就是说,在定子αβ静止坐标系,转子和定子的物理量具有相同的频率。
整理电压方程的矢量形式如下:
{
u
⃗
s
=
R
s
i
⃗
s
+
d
d
t
ψ
⃗
s
u
⃗
r
=
R
r
i
⃗
r
+
d
d
t
ψ
⃗
r
−
j
ω
r
ψ
⃗
r
\begin{cases} \vec{u}_s=R_s\vec{i}_s+\frac{d}{dt}\vec{\psi}_s \\ \vec{u}_r=R_r\vec{i}_r+\frac{d}{dt}\vec{\psi}_r-j\omega_r\vec{\psi}_r \end{cases}
{us=Rsis+dtdψsur=Rrir+dtdψr−jωrψr
电压方程(αβ形式)
让矢量的实部和虚部分别相等,把电压方程写成αβ形式:
{
u
s
α
=
R
s
i
s
α
+
d
d
t
ψ
s
α
u
s
β
=
R
s
i
s
β
+
d
d
t
ψ
s
β
u
r
α
=
R
r
i
r
α
+
d
d
t
ψ
r
α
+
ω
r
ψ
r
β
u
r
β
=
R
r
i
r
β
+
d
d
t
ψ
r
β
−
ω
r
ψ
r
α
\begin{cases} u_{s\alpha} &= R_si_{s\alpha}+\frac{d}{dt}\psi_{s\alpha}\\ u_{s\beta} &= R_si_{s\beta}+\frac{d}{dt}\psi_{s\beta}\\ u_{r\alpha} &= R_ri_{r\alpha}+\frac{d}{dt}\psi_{r\alpha}+\omega_r\psi_{r\beta}\\ u_{r\beta} &= R_ri_{r\beta}+\frac{d}{dt}\psi_{r\beta}-\omega_r\psi_{r\alpha} \end{cases}
⎩
⎨
⎧usαusβurαurβ=Rsisα+dtdψsα=Rsisβ+dtdψsβ=Rrirα+dtdψrα+ωrψrβ=Rrirβ+dtdψrβ−ωrψrα
注意转子电压方程中的耦合项。
磁链方程(αβ形式)
磁链方程不知道怎么样直接用矢量来做。。所以还是先αβ形式再矢量形式吧。
这个计算过程在第十三讲 等幅值坐标变换矩阵解释及双馈异步电机的定子侧两相静止模型中有更简洁的说明,这边补充了一下计算过程。
对比矢量形式和矩阵形式(其中 ω r t = θ r \omega_r t=\theta_r ωrt=θr)
i
⃗
r
=
e
j
θ
r
i
⃗
r
r
,
i
⃗
r
r
=
e
−
j
θ
r
i
⃗
r
r
i
r
α
β
=
T
r
(
θ
r
)
i
r
r
,
i
r
r
=
T
r
(
−
θ
r
)
i
r
α
β
\begin{align*} \vec{i}_{r}&=e^{j\theta_r}\vec{i}_{r}^r,\quad\; \vec{i}_{r}^r=e^{-j\theta_r}\vec{i}_{r}^r \\ \boldsymbol{i}_{r\alpha\beta}&=T_{r}(\theta_r)\boldsymbol{i}_{r}^r, \; \boldsymbol{i}_{r}^r = T_{r}(-\theta_r)\boldsymbol{i}_{r\alpha\beta} \end{align*}
irirαβ=ejθrirr,irr=e−jθrirr=Tr(θr)irr,irr=Tr(−θr)irαβ
其中,
T
r
(
θ
r
)
T_{r}(\theta_r)
Tr(θr)实现逆时针旋转
θ
r
\theta_r
θr(park反变换),
T
r
(
−
θ
r
)
T_{r}(-\theta_r)
Tr(−θr)实现顺时针旋转
θ
r
\theta_r
θr(park变换)。(都写成3x3矩阵,便于运算)
T r ( θ r ) = [ c o s θ r − s i n θ r 0 s i n θ r c o s θ r 0 0 0 1 ] , ( inverse Park ) T r ( − θ r ) = [ c o s θ r s i n θ r 0 − s i n θ r c o s θ r 0 0 0 1 ] , ( Park ) T r − 1 ( θ r ) = T r ( − θ r ) \begin{align*} T_{r}(\theta_r) &= \left[\begin{matrix} cos\theta_r & -sin\theta_r & 0\\ sin\theta_r & cos\theta_r & 0 \\ 0 & 0 & 1 \end{matrix} \right], \;(\text{inverse\,Park}) \\ T_{r}(-\theta_r) &= \left[\begin{matrix} cos\theta_r & sin\theta_r & 0\\ -sin\theta_r & cos\theta_r & 0 \\ 0 & 0 & 1 \end{matrix} \right], \;(\text{Park}) \\ T_{r}^{-1}(\theta_r) &= T_{r}(-\theta_r) \end{align*} Tr(θr)Tr(−θr)Tr−1(θr)= cosθrsinθr0−sinθrcosθr0001 ,(inversePark)= cosθr−sinθr0sinθrcosθr0001 ,(Park)=Tr(−θr)
补充一些用到的式子:
- 矩阵乘法: M T A B = M T A [ ( M T ) − 1 M T ] B = M T A T − 1 M − 1 ( M T B ) MTAB=MTA[(MT)^{-1}MT]B=MTAT^{-1}M^{-1}(MTB) MTAB=MTA[(MT)−1MT]B=MTAT−1M−1(MTB)
- 定子侧物理量的Clarke变换: T 3 / 2 x s = x s α β T_{3/2}\boldsymbol{x}_s=\boldsymbol{x}_{s\alpha\beta} T3/2xs=xsαβ
- 转子侧物理量的Clarke变换: T 3 / 2 x r = x r α β r T_{3/2}\boldsymbol{x}_r=\boldsymbol{x}_{r\alpha\beta}^r T3/2xr=xrαβr
- 转子侧物理量Clarke变换后,再变换到定子αβ坐标系上: T r ( θ r ) T 3 / 2 x r = T r ( θ r ) x r α β r = x r α β T_r({\theta_r})T_{3/2}\boldsymbol{x}_r=T_r({\theta_r})\boldsymbol{x}_{r\alpha\beta}^r=\boldsymbol{x}_{r\alpha\beta} Tr(θr)T3/2xr=Tr(θr)xrαβr=xrαβ
- 转子DQ坐标系和定子αβ坐标系物理量的关系: x r α β r = T r ( − θ r ) x r α β \boldsymbol{x}_{r\alpha\beta}^r=T_{r}(-\theta_r)\boldsymbol{x}_{r\alpha\beta} xrαβr=Tr(−θr)xrαβ
之前三相坐标系下的磁链表达式为:
[
ψ
s
ψ
r
]
=
[
L
s
s
L
s
r
(
θ
r
)
L
r
s
(
θ
r
)
L
r
r
]
[
i
s
i
r
]
\left[\begin{matrix} \boldsymbol{\psi}_s \\ \boldsymbol{\psi}_r \end{matrix}\right] = \left[\begin{matrix} \boldsymbol{L}_{ss} & \boldsymbol{L}_{sr}(\theta_r) \\ \boldsymbol{L}_{rs}(\theta_r) & \boldsymbol{L}_{rr} \end{matrix}\right] \left[\begin{matrix} \boldsymbol{i}_s \\ \boldsymbol{i}_r \end{matrix}\right]
[ψsψr]=[LssLrs(θr)Lsr(θr)Lrr][isir]
先把定子磁链变换到定子αβ坐标系
ψ
s
α
β
\boldsymbol{\psi}_{s\alpha\beta}
ψsαβ(注意其中转子电流的表达式):
ψ
s
α
β
=
T
3
/
2
ψ
s
=
T
3
/
2
L
s
s
T
3
/
2
−
1
(
T
3
/
2
i
s
)
+
T
3
/
2
L
s
r
(
θ
r
)
T
3
/
2
−
1
(
T
3
/
2
i
r
)
=
T
3
/
2
L
s
s
T
3
/
2
−
1
i
s
α
β
+
T
3
/
2
L
s
r
(
θ
r
)
T
3
/
2
−
1
i
r
α
β
r
=
(
T
3
/
2
L
s
s
T
3
/
2
−
1
)
i
s
α
β
+
[
T
3
/
2
L
s
r
(
θ
r
)
T
3
/
2
−
1
T
r
(
−
θ
r
)
]
i
r
α
β
\begin{align*} \boldsymbol{\psi}_{s\alpha\beta}=T_{3/2}\boldsymbol{\psi}_s &= T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1}(T_{3/2}\boldsymbol{i}_s) +T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}(T_{3/2}\boldsymbol{i}_r) \\ &=T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1}\boldsymbol{i}_{s\alpha\beta}+ T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}\boldsymbol{i}_{r\alpha\beta}^r \\ &=(T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1})\boldsymbol{i}_{s\alpha\beta}+ \left[T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}T_{r}(-\theta_r) \right]\boldsymbol{i}_{r\alpha\beta} \\ \end{align*}
ψsαβ=T3/2ψs=T3/2LssT3/2−1(T3/2is)+T3/2Lsr(θr)T3/2−1(T3/2ir)=T3/2LssT3/2−1isαβ+T3/2Lsr(θr)T3/2−1irαβr=(T3/2LssT3/2−1)isαβ+[T3/2Lsr(θr)T3/2−1Tr(−θr)]irαβ
其中,两个电感矩阵在变换后变为:
T
3
/
2
L
s
s
T
3
/
2
−
1
=
[
1.5
L
m
+
L
l
s
0
0
0
1.5
L
m
+
L
l
s
0
0
0
L
l
s
]
T
3
/
2
L
s
r
(
θ
r
)
T
3
/
2
−
1
T
r
(
−
θ
r
)
=
[
1.5
L
m
0
0
0
1.5
L
m
0
0
0
0
]
\begin{align*} T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1} &= \left[\begin{matrix} 1.5L_m+L_{ls} & 0 & 0 \\ 0 & 1.5L_m+L_{ls} & 0 \\ 0 & 0 & L_{ls} \end{matrix}\right] \\ T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}T_{r}(-\theta_r) &= \left[\begin{matrix} 1.5L_m & 0 & 0 \\ 0 & 1.5L_m & 0 \\ 0 & 0 & 0 \end{matrix}\right] \\ \end{align*}
T3/2LssT3/2−1T3/2Lsr(θr)T3/2−1Tr(−θr)=
1.5Lm+Lls0001.5Lm+Lls000Lls
=
1.5Lm0001.5Lm0000
在mathCAD中的计算结果:
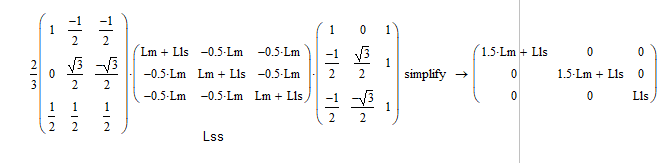
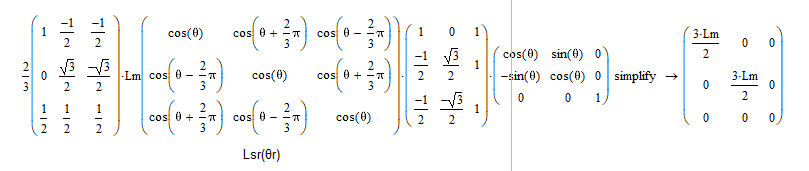
第二行,转子磁链
ψ
r
α
β
\boldsymbol{\psi}_{r\alpha\beta}
ψrαβ,需要在Clark变换后,再转过
θ
r
\theta_r
θr(左乘
T
r
(
θ
r
)
T_{r}(\theta_r)
Tr(θr)),才转换到αβ定子坐标系下。
ψ
r
α
β
=
T
r
(
θ
r
)
ψ
r
α
β
r
=
T
r
(
θ
r
)
T
3
/
2
ψ
r
=
T
r
(
θ
r
)
T
3
/
2
L
r
s
(
θ
r
)
T
3
/
2
−
1
(
T
3
/
2
i
s
)
+
[
T
r
(
θ
r
)
T
3
/
2
L
r
r
T
3
/
2
−
1
T
r
(
−
θ
r
)
]
[
T
r
(
θ
r
)
T
3
/
2
i
r
]
=
T
r
(
θ
r
)
T
3
/
2
L
r
s
(
θ
r
)
T
3
/
2
−
1
i
s
α
β
+
[
T
r
(
θ
r
)
T
3
/
2
L
r
r
T
3
/
2
−
1
T
r
(
−
θ
r
)
]
i
r
α
β
\begin{align*} \boldsymbol{\psi}_{r\alpha\beta} &= T_{r}(\theta_r)\boldsymbol{\psi}_{r\alpha\beta}^r =T_{r}(\theta_r)T_{3/2}\boldsymbol{\psi}_r \\ &= T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rs}(\theta_r) T_{3/2}^{-1}(T_{3/2}\boldsymbol{i}_s) + \left[T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rr}T_{3/2}^{-1}T_{r}(-\theta_r)\right] \left[ T_{r}(\theta_r)T_{3/2}\boldsymbol{i}_r \right]\\ &= T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rs}(\theta_r) T_{3/2}^{-1}\boldsymbol{i}_{s\alpha\beta} + \left[T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rr}T_{3/2}^{-1}T_{r}(-\theta_r)\right] \boldsymbol{i}_{r\alpha\beta}\\ \end{align*}
ψrαβ=Tr(θr)ψrαβr=Tr(θr)T3/2ψr=Tr(θr)T3/2Lrs(θr)T3/2−1(T3/2is)+[Tr(θr)T3/2LrrT3/2−1Tr(−θr)][Tr(θr)T3/2ir]=Tr(θr)T3/2Lrs(θr)T3/2−1isαβ+[Tr(θr)T3/2LrrT3/2−1Tr(−θr)]irαβ
其中,两个电感矩阵在变换后变为:
T
r
(
θ
r
)
T
3
/
2
L
r
s
(
θ
r
)
T
3
/
2
−
1
=
[
1.5
L
m
0
0
0
1.5
L
m
0
0
0
0
]
T
r
(
θ
r
)
T
3
/
2
L
r
r
T
3
/
2
−
1
T
r
(
−
θ
r
)
=
[
1.5
L
m
+
L
l
r
0
0
0
1.5
L
m
+
L
l
r
0
0
0
L
l
r
]
\begin{align*} T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rs}(\theta_r) T_{3/2}^{-1} &= \left[\begin{matrix} 1.5L_m & 0 & 0 \\ 0 & 1.5L_m & 0 \\ 0 & 0 & 0 \end{matrix}\right] \\ T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rr}T_{3/2}^{-1}T_{r}(-\theta_r) &= \left[\begin{matrix} 1.5L_m+L_{lr} & 0 & 0 \\ 0 & 1.5L_m+L_{lr} & 0 \\ 0 & 0 & L_{lr} \end{matrix}\right] \\ \end{align*}
Tr(θr)T3/2Lrs(θr)T3/2−1Tr(θr)T3/2LrrT3/2−1Tr(−θr)=
1.5Lm0001.5Lm0000
=
1.5Lm+Llr0001.5Lm+Llr000Llr
在mathCAD中的计算结果:
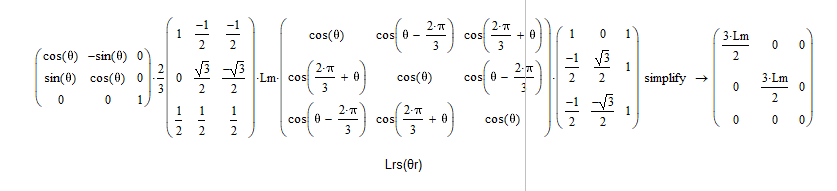
(第二个矩阵表达式比较长,分两步计算)

只看前两行,这些电感矩阵在变换后都变成了对角矩阵,并且系数都变成了常数(不再有 c o s ( θ r ) cos(\theta_r) cos(θr)项),模型得到了简化。
{ ψ s α = ( 1.5 L m + L l s ) i s α + 1.5 L m i r α = L s i s α + L M i r α ψ s β = ( 1.5 L m + L l s ) i s β + 1.5 L m i r β = L s i s β + L M i r β ψ r α = ( 1.5 L m + L l r ) i r α + 1.5 L m i s α = L r i r α + L M i s α ψ r β = ( 1.5 L m + L l r ) i r β + 1.5 L m i s β = L r i r β + L M i s β \begin{cases} \psi_{s\alpha} &= (1.5L_m+L_{ls})i_{s\alpha}+1.5L_mi_{r\alpha} =L_si_{s\alpha}+L_Mi_{r\alpha}\\ \psi_{s\beta} &= (1.5L_m+L_{ls})i_{s\beta}+1.5L_mi_{r\beta} =L_si_{s\beta}+L_Mi_{r\beta}\\ \psi_{r\alpha} &= (1.5L_m+L_{lr})i_{r\alpha}+1.5L_mi_{s\alpha} =L_ri_{r\alpha}+L_Mi_{s\alpha}\\ \psi_{r\beta} &= (1.5L_m+L_{lr})i_{r\beta}+1.5L_mi_{s\beta} =L_ri_{r\beta}+L_Mi_{s\beta} \end{cases} ⎩ ⎨ ⎧ψsαψsβψrαψrβ=(1.5Lm+Lls)isα+1.5Lmirα=Lsisα+LMirα=(1.5Lm+Lls)isβ+1.5Lmirβ=Lsisβ+LMirβ=(1.5Lm+Llr)irα+1.5Lmisα=Lrirα+LMisα=(1.5Lm+Llr)irβ+1.5Lmisβ=Lrirβ+LMisβ
磁链方程(矢量形式)
根据磁链方程的αβ形式可以写出矢量形式。
{ ψ ⃗ s = L s i ⃗ s + L M i ⃗ r ψ ⃗ r = L r i ⃗ r + L M i ⃗ s \begin{cases} \vec{\psi}_{s} &=L_s\vec{i}_{s}+L_M\vec{i}_{r}\\ \vec{\psi}_{r} &=L_r\vec{i}_{r}+L_M\vec{i}_{s} \end{cases} {ψsψr=Lsis+LMir=Lrir+LMis
dq坐标系模型
回顾之前的推导,在定子αβ静止坐标系,转子和定子的物理量具有相同的频率,也就是
ω
e
\omega_e
ωe。所以,在dq坐标系的转速为
ω
e
\omega_e
ωe时,
一些物理量会变成直流量,便于控制。之前也提到了,让坐标轴逆时针旋转
ω
e
t
\omega_e t
ωet,就是把对应的物理量顺时针旋转
ω
e
t
\omega_e t
ωet,也就是
e
−
j
ω
t
x
⃗
e^{-j\omega t}\vec{x}
e−jωtx
另外需要说明的是,不管dq坐标系的旋转速度是多少,表达式都是一样的,只是其中的
ω
e
\omega_e
ωe值改变。
矢量形式
把定子αβ静止坐标系的电压方程两边都乘以
e
−
j
ω
t
e^{-j\omega t}
e−jωt,得到# dq坐标系下的电压方程:
电压方程中,
e
−
j
ω
t
u
⃗
s
=
u
⃗
s
a
e^{-j\omega t}\vec{u}_s=\vec{u}_s^a
e−jωtus=usa。上标a代表dq轴下的物理量。
注意对于磁链的微分,略有不同,之前推导过:
e
−
j
ω
e
t
d
d
t
ψ
⃗
=
d
d
t
ψ
⃗
a
+
j
ω
e
ψ
⃗
a
e^{-j\omega_e t}\frac{d}{dt}\vec{\psi}=\frac{d}{dt}\vec{\psi}^a+j\omega_e\vec{\psi}^a
e−jωetdtdψ=dtdψa+jωeψa
记得角速度的关系:
ω
e
=
ω
s
1
+
ω
r
\omega_e=\omega_{s1}+\omega_{r}
ωe=ωs1+ωr,电网速度=转差速度+转子电角速度。其中,转子物理量(电压、电流、磁链)的角速度就是转差速度
ω
s
1
\omega_{s1}
ωs1,所以这个方程是还挺对称的。
{
u
⃗
s
a
=
R
s
i
⃗
s
a
+
d
d
t
ψ
⃗
s
a
+
j
ω
e
ψ
⃗
s
a
u
⃗
r
a
=
R
r
i
⃗
r
a
+
d
d
t
ψ
⃗
r
a
+
j
(
ω
e
−
ω
r
)
ψ
⃗
r
a
=
R
r
i
⃗
r
a
+
d
d
t
ψ
⃗
r
a
+
j
ω
s
1
ψ
⃗
r
a
\begin{cases} \vec{u}_s^a=R_s\vec{i}_s^a+\frac{d}{dt}\vec{\psi}_s^a+j\omega_e \vec{\psi}_s^a \\ \vec{u}_r^a=R_r\vec{i}_r^a+\frac{d}{dt}\vec{\psi}_r^a+j(\omega_e-\omega_r)\vec{\psi}_r^a = R_r\vec{i}_r^a+\frac{d}{dt}\vec{\psi}_r^a+j\omega_{s1}\vec{\psi}_r^a \end{cases}
{usa=Rsisa+dtdψsa+jωeψsaura=Rrira+dtdψra+j(ωe−ωr)ψra=Rrira+dtdψra+jωs1ψra
磁链方程形式没有变,只是上标加了个a,表示是dq轴下的量。
{ ψ ⃗ s a = L s i ⃗ s a + L M i ⃗ r a ψ ⃗ r a = L r i ⃗ r a + L M i ⃗ s a \begin{cases} \vec{\psi}_{s}^a &=L_s\vec{i}_{s}^a+L_M\vec{i}_{r}^a\\ \vec{\psi}_{r}^a &=L_r\vec{i}_{r}^a+L_M\vec{i}_{s}^a \end{cases} {ψsaψra=Lsisa+LMira=Lrira+LMisa
dq形式
根据矢量形式,同样可以写出dq形式。
电压方程:
{
u
s
d
=
R
s
i
s
d
+
d
d
t
ψ
s
d
−
ω
e
ψ
s
q
u
s
q
=
R
s
i
s
q
+
d
d
t
ψ
s
q
+
ω
e
ψ
s
d
u
r
d
=
R
r
i
r
d
+
d
d
t
ψ
r
d
−
ω
s
1
ψ
r
q
u
r
q
=
R
r
i
r
q
+
d
d
t
ψ
r
q
+
ω
s
1
ψ
r
d
\begin{cases} u_{sd} &= R_si_{sd}+\frac{d}{dt}\psi_{sd}-\omega_e\psi_{sq}\\ u_{sq} &= R_si_{sq}+\frac{d}{dt}\psi_{sq}+\omega_e\psi_{sd}\\ u_{rd} &= R_ri_{rd}+\frac{d}{dt}\psi_{rd}-\omega_{s1}\psi_{rq}\\ u_{rq} &= R_ri_{rq}+\frac{d}{dt}\psi_{rq}+\omega_{s1}\psi_{rd} \end{cases}
⎩
⎨
⎧usdusqurdurq=Rsisd+dtdψsd−ωeψsq=Rsisq+dtdψsq+ωeψsd=Rrird+dtdψrd−ωs1ψrq=Rrirq+dtdψrq+ωs1ψrd
磁链方程:
{
ψ
s
d
=
L
s
i
s
d
+
L
M
i
r
d
ψ
s
q
=
L
s
i
s
q
+
L
M
i
r
q
ψ
r
d
=
L
r
i
r
d
+
L
M
i
s
d
ψ
r
q
=
L
r
i
r
q
+
L
M
i
s
q
\begin{cases} \psi_{sd} &=L_si_{sd}+L_Mi_{rd}\\ \psi_{sq} &=L_si_{sq}+L_Mi_{rq}\\ \psi_{rd} &=L_ri_{rd}+L_Mi_{sd}\\ \psi_{rq} &=L_ri_{rq}+L_Mi_{sq} \end{cases}
⎩
⎨
⎧ψsdψsqψrdψrq=Lsisd+LMird=Lsisq+LMirq=Lrird+LMisd=Lrirq+LMisq
参考资料
- 第十一讲 风力发电系统基本结构+双馈电机数学模型第一部分_哔哩哔哩_bilibili11~16讲和DFIG有关,可以看下。
- G. Abad, J. Lopez, M. Rodriguez, L. Marroyo, and G. Iwanski, Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation. John Wiley & Sons, 2011.
- 自己买的中文书,讲得比较简略,如果只看这两本,我是看不懂的:
- 马宏伟,风力发电系统控制原理
- 王毅,风力发电系统的建模与仿真