由于本文公式所占用的字符比较多,无法在一篇博客中完整发布,所以将其分为两篇博客。本篇主要介绍了离散傅里叶变换 DFT 的内容,以及相关的总结。对于前置内容,包括傅里叶级数 FS,连续时间傅里叶变换 CTFT,以及离散时间傅里叶变换 DTFT 等,请移步以下链接。
傅里叶级数FS,连续时间傅里叶变换CTFT,离散时间傅里叶变换DTFT,离散傅里叶变换DFT,推导与联系(一)
https://blog.csdn.net/qq_33552519/article/details/130255215
对于离散傅里叶变换所衍生出的离散余弦变换和离散正弦变换,在我的另一篇文章中有所介绍,欢迎阅读与提出相关修改意见。
- DFT:https://blog.csdn.net/qq_33552519/article/details/124917126
- DCT:https://blog.csdn.net/qq_33552519/article/details/124917473
- DST:https://blog.csdn.net/qq_33552519/article/details/124962042
4 离散傅里叶变换
在前面的章节中,我们从周期函数的傅里叶级数扩展到了非周期函数的傅里叶变换,再从非周期函数的傅里叶变换扩展到了离散序列的离散时间傅里叶变换。然而对比三者可以发现,只有离散时间傅里叶变换的时域是离散的,而只有傅里叶级数的频域是离散的,并不存在一种变换的时域和频域都是离散的,这意味着它们都不适合数字计算机的处理。为了克服这种问题,一种自然而然的想法就是综合傅里叶级数的频域与离散时间傅里叶变换的时域,这就引出了我们接下来所要讨论的离散傅里叶变换。
对于一个定义在有限区间 t ∈ ( 0 , T ) t \in \left( {0,T} \right) t∈(0,T) 上的连续时间函数 f a ( t ) {f_a}\left( t \right) fa(t),对其以 T T T 为周期进行周期性延拓,得到周期函数 f ~ a ( t ) {\tilde f_a}\left( t \right) f~a(t),其中
f ~ a ( t + n T ) = f a ( t ) , − ∞ < n < ∞ . (4.1) {\tilde f_a}\left( {t + nT} \right) = {f_a}\left( t \right),\quad - \infty < n < \infty . \tag{4.1} f~a(t+nT)=fa(t),−∞<n<∞.(4.1)
那么可得 f a ( t ) {f_a}\left( t \right) fa(t) 的连续时间傅里叶变换 F a ( j Ω ) {F_a}\left( {j\Omega } \right) Fa(jΩ) 与 f ~ a ( t ) {\tilde f_a}\left( t \right) f~a(t) 的傅里叶级数系数 F ~ a [ n ] {\tilde F_a}\left[ n \right] F~a[n] 分别为
F a ( j Ω ) = ∫ 0 T f a ( t ) e − j Ω t d t , F ~ a [ n ] = 1 T ∫ 0 T f ~ a ( t ) e − j n Ω T t d t = 1 T F a ( j n Ω T ) , w h e r e Ω T = 2 π / T . (4.2) \begin{gathered} {F_a}\left( {j\Omega } \right) = \int\limits_0^T {{f_a}\left( t \right){e^{ - j\Omega t}}dt} , \\ {{\tilde F}_a}\left[ n \right] = \frac{1}{T}\int\limits_0^T {{{\tilde f}_a}\left( t \right){e^{ - jn{\Omega _T}t}}dt} = \frac{1}{T}{F_a}\left( {jn{\Omega _T}} \right), \\ where\;{\Omega _T} = 2\pi /T. \\ \end{gathered} \tag{4.2} Fa(jΩ)=0∫Tfa(t)e−jΩtdt,F~a[n]=T10∫Tf~a(t)e−jnΩTtdt=T1Fa(jnΩT),whereΩT=2π/T.(4.2)
也就是说,周期函数的傅里叶级数系数实际上是该周期函数在一个周期内的傅里叶变换以 Ω T = 2 π / T {\Omega _T} = 2\pi /T ΩT=2π/T 为间隔均匀采样与幅度缩放的结果。在讨论离散时间傅里叶变换时就可以发现,在时域中对连续时间函数以 T T T 为间隔均匀采样会导致该函数的傅里叶变换以 Ω T {\Omega _T} ΩT 为周期进行延拓与叠加。那以相反的视角来看式 (4.2),是否是因为 f a ( t ) {f_a}\left( t \right) fa(t) 的傅里叶变换 F a ( j Ω ) {F_a}\left( {j\Omega } \right) Fa(jΩ) 以 Ω T {\Omega _T} ΩT 为间隔均匀采样,导致了 f a ( t ) {f_a}\left( t \right) fa(t) 在时域以 T T T 为周期进行延拓与叠加从而获得了周期函数 f ~ a ( t ) {\tilde f_a}\left( t \right) f~a(t) 呢?而且因为 f a ( t ) {f_a}\left( t \right) fa(t) 只在 t ∈ ( 0 , T ) t \in \left( {0,T} \right) t∈(0,T) 上的区间定义,所以以 T T T 为周期进行周期延拓所获得的周期函数 f ~ a ( t ) {\tilde f_a}\left( t \right) f~a(t) 可以完整地恢复 f a ( t ) {f_a}\left( t \right) fa(t),不会造成信息失真。
由于一般的连续时间函数的傅里叶变换通常不具有周期性,且在整个频率数轴 Ω ∈ ( − ∞ , + ∞ ) \Omega \in \left( { - \infty , + \infty } \right) Ω∈(−∞,+∞) 上都有定义,所以讨论其频域的采样对于计算机的实用性并不具有太大意义。然而,对于连续时间函数经过均匀采样所获得的离散时域序列,其离散时间傅里叶变换则以 2 π 2\pi 2π 为周期,因此在 2 π 2\pi 2π 的范围内对其进行采样,即可获得有限长度的频域离散序列。如果限制时域序列的长度,即可满足计算机对时域与频域转换的可实现性。为此,接下来我们主要基于离散时间序列及其离散时间傅里叶变换进行讨论。
对于离散序列 f [ n ] f\left[ n \right] f[n],其离散时间傅里叶变换为
F ( e j ω ) = ∑ n = − ∞ ∞ f [ n ] e − j ω n . (4.3) F\left( {{e^{j\omega }}} \right) = \sum\limits_{n = - \infty }^\infty {f\left[ n \right]{e^{ - j\omega n}}} .\tag{4.3} F(ejω)=n=−∞∑∞f[n]e−jωn.(4.3)
对 F ( e j ω ) F\left( {{e^{j\omega }}} \right) F(ejω) 以 2 π / M 2\pi /M 2π/M 为间隔均匀采样,其中 M M M 为正整数。 类似于连续时间信号采样,引入周期冲激串
p ( ω ) = ∑ k = − ∞ ∞ δ ( ω − 2 π k M ) . (4.4) p\left( \omega \right) = \sum\limits_{k = - \infty }^\infty {\delta \left( {\omega - \frac{{2\pi k}}{M}} \right)} .\tag{4.4} p(ω)=k=−∞∑∞δ(ω−M2πk).(4.4)
则 F ( e j ω ) F\left( {{e^{j\omega }}} \right) F(ejω) 采样所得结果可表示为
G ( e j ω ) = F ( e j ω ) p ( ω ) = ∑ k = − ∞ ∞ F ( e j 2 π k M ) δ ( ω − 2 π k M ) . (4.5) G\left( {{e^{j\omega }}} \right) = F\left( {{e^{j\omega }}} \right)p\left( \omega \right) = \sum\limits_{k = - \infty }^\infty {F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right)\delta \left( {\omega - \frac{{2\pi k}}{M}} \right)} . \tag{4.5} G(ejω)=F(ejω)p(ω)=k=−∞∑∞F(ejM2πk)δ(ω−M2πk).(4.5)
因为 G ( e j ω ) G\left( {{e^{j\omega }}} \right) G(ejω) 是由狄拉克函数定义的,在推导其离散时间傅里叶反变换时在积分边界上会存在一点问题。因为 G ( e j ω ) G\left( {{e^{j\omega }}} \right) G(ejω) 是以 2 π 2\pi 2π 为周期的,且反变换的积分周期位置不影响结果,所以我们不妨在 ω ∈ ( 0 − , 2 π − ) \omega \in \left( {{0^ - },2{\pi ^ - }} \right) ω∈(0−,2π−) 上进行积分,即积分边界是通过左侧极限来定义的,于是有
g [ m ] = 1 2 π ∫ 0 − 2 π − F p ( e j ω ) e j ω m d ω = 1 2 π ∫ 0 − 2 π − [ ∑ k = − ∞ ∞ F ( e j 2 π k M ) δ ( ω − 2 π k M ) ] e j ω m d ω = 1 2 π ∫ 0 − 2 π − [ ∑ k = 0 M − 1 F ( e j 2 π k M ) δ ( ω − 2 π k M ) ] e j ω m d ω = 1 2 π ∑ k = 0 M − 1 F ( e j 2 π k M ) ∫ 0 − 2 π − δ ( ω − 2 π k M ) e j ω m d ω = 1 2 π ∑ k = 0 M − 1 F ( e j 2 π k M ) e j 2 π k m M . (4.6) \begin{aligned} g\left[ m \right] &= \frac{1}{{2\pi }}\int\limits_{{0^ - }}^{2{\pi ^ - }} {{F_p}\left( {{e^{j\omega }}} \right){e^{j\omega m}}d\omega } \\ &= \frac{1}{{2\pi }}\int\limits_{{0^ - }}^{2{\pi ^ - }} {\left[ {\sum\limits_{k = - \infty }^\infty {F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right)\delta \left( {\omega - \frac{{2\pi k}}{M}} \right)} } \right]{e^{j\omega m}}d\omega } \\ &= \frac{1}{{2\pi }}\int\limits_{{0^ - }}^{2{\pi ^ - }} {\left[ {\sum\limits_{k = 0}^{M - 1} {F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right)\delta \left( {\omega - \frac{{2\pi k}}{M}} \right)} } \right]{e^{j\omega m}}d\omega } \\ &= \frac{1}{{2\pi }}\sum\limits_{k = 0}^{M - 1} {F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right)\int\limits_{{0^ - }}^{2{\pi ^ - }} {\delta \left( {\omega - \frac{{2\pi k}}{M}} \right){e^{j\omega m}}d\omega } } \\ &= \frac{1}{{2\pi }}\sum\limits_{k = 0}^{M - 1} {F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right){e^{j\tfrac{{2\pi km}}{M}}}} . \\ \end{aligned} \tag{4.6} g[m]=2π10−∫2π−Fp(ejω)ejωmdω=2π10−∫2π−[k=−∞∑∞F(ejM2πk)δ(ω−M2πk)]ejωmdω=2π10−∫2π−[k=0∑M−1F(ejM2πk)δ(ω−M2πk)]ejωmdω=2π1k=0∑M−1F(ejM2πk)0−∫2π−δ(ω−M2πk)ejωmdω=2π1k=0∑M−1F(ejM2πk)ejM2πkm.(4.6)
可以发现,式 (4.6) 所表示的离散时间傅里叶反变换成为了一个只涉及有限项 M M M 项的求和运算。为了建立起 G ( e j ω ) G\left( {{e^{j\omega }}} \right) G(ejω) 的离散傅里叶反变换序列 g [ m ] g\left[ m \right] g[m] 与原始序列 f [ n ] f\left[ n \right] f[n] 的联系,将 F ( e j 2 π k M ) F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right) F(ejM2πk) 代入式 (4.6) 可得
g [ m ] = 1 2 π ∑ k = 0 M − 1 F ( e j 2 π k M ) e j 2 π k m M = 1 2 π ∑ k = 0 M − 1 ( ∑ n = − ∞ ∞ f [ n ] e − j 2 π k M n ) e j 2 π k m M = 1 2 π ∑ n = − ∞ ∞ f [ n ] ( ∑ k = 0 M − 1 e j 2 π k M ( m − n ) ) . (4.7) \begin{aligned} g\left[ m \right] &= \frac{1}{{2\pi }}\sum\limits_{k = 0}^{M - 1} {F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right){e^{j\tfrac{{2\pi km}}{M}}}} \\ &= \frac{1}{{2\pi }}\sum\limits_{k = 0}^{M - 1} {\left( {\sum\limits_{n = - \infty }^\infty {f\left[ n \right]{e^{ - j\tfrac{{2\pi k}}{M}n}}} } \right){e^{j\tfrac{{2\pi km}}{M}}}} \\ &= \frac{1}{{2\pi }}\sum\limits_{n = - \infty }^\infty {f\left[ n \right]\left( {\sum\limits_{k = 0}^{M - 1} {{e^{j\tfrac{{2\pi k}}{M}\left( {m - n} \right)}}} } \right)} . \\ \end{aligned} \tag{4.7} g[m]=2π1k=0∑M−1F(ejM2πk)ejM2πkm=2π1k=0∑M−1(n=−∞∑∞f[n]e−jM2πkn)ejM2πkm=2π1n=−∞∑∞f[n](k=0∑M−1ejM2πk(m−n)).(4.7)
当 m − n = p M m - n = pM m−n=pM,其中 p p p 为整数时,可得
∑ k = 0 M − 1 e j 2 π k M ( m − n ) = ∑ k = 0 M − 1 e j 2 π k M p M = M . (4.8) \sum\limits_{k = 0}^{M - 1} {{e^{j\tfrac{{2\pi k}}{M}\left( {m - n} \right)}}} = \sum\limits_{k = 0}^{M - 1} {{e^{j\tfrac{{2\pi k}}{M}pM}}} = M.\tag{4.8} k=0∑M−1ejM2πk(m−n)=k=0∑M−1ejM2πkpM=M.(4.8)
而当 m − n = p M + q m - n = pM + q m−n=pM+q,其中 p , q p,q p,q 为整数,且 1 ⩽ q ⩽ M − 1 1 \leqslant q \leqslant M - 1 1⩽q⩽M−1 时,可得
∑ k = 0 M − 1 e j 2 π k M ( m − n ) = ∑ k = 0 M − 1 e j 2 π k M ( p M + q ) = ∑ k = 0 M − 1 ( e j 2 π q M ) k = 1 − ( e j 2 π q M ) M 1 − e j 2 π q M = 1 − e j 2 π q 1 − e j 2 π q M = 0. (4.9) \begin{gathered} \sum\limits_{k = 0}^{M - 1} {{e^{j\tfrac{{2\pi k}}{M}\left( {m - n} \right)}}} = \sum\limits_{k = 0}^{M - 1} {{e^{j\tfrac{{2\pi k}}{M}\left( {pM + q} \right)}}} = \sum\limits_{k = 0}^{M - 1} {{{\left( {{e^{j\tfrac{{2\pi q}}{M}}}} \right)}^k}} \\ = \frac{{1 - {{\left( {{e^{j\tfrac{{2\pi q}}{M}}}} \right)}^M}}}{{1 - {e^{j\tfrac{{2\pi q}}{M}}}}} = \frac{{1 - {e^{j2\pi q}}}}{{1 - {e^{j\tfrac{{2\pi q}}{M}}}}} = 0. \\ \end{gathered} \tag{4.9} k=0∑M−1ejM2πk(m−n)=k=0∑M−1ejM2πk(pM+q)=k=0∑M−1(ejM2πq)k=1−ejM2πq1−(ejM2πq)M=1−ejM2πq1−ej2πq=0.(4.9)
于是可得恒等式
∑ k = 0 M − 1 e j 2 π k M ( m − n ) = { M , m − n = p M , p ∈ Z , 0 , o t h e r s . (4.10) \sum\limits_{k = 0}^{M - 1} {{e^{j\tfrac{{2\pi k}}{M}\left( {m - n} \right)}}} = \left\{ {\begin{array}{c} {M,}&{m - n = pM,\;p \in \mathbb{Z},} \\ {0,}&{others.} \end{array}} \right.\tag{4.10} k=0∑M−1ejM2πk(m−n)={M,0,m−n=pM,p∈Z,others.(4.10)
或者利用冲激序列的定义写为
∑ k = 0 M − 1 e j 2 π k M ( m − n ) = M ∑ p = − ∞ ∞ δ [ m − n + p M ] . (4.11) \sum\limits_{k = 0}^{M - 1} {{e^{j\tfrac{{2\pi k}}{M}\left( {m - n} \right)}}} = M\sum\limits_{p = - \infty }^\infty {\delta \left[ {m - n + pM} \right]} .\tag{4.11} k=0∑M−1ejM2πk(m−n)=Mp=−∞∑∞δ[m−n+pM].(4.11)
因此,式 (4.7) 可改写为
g [ m ] = 1 2 π ∑ k = 0 M − 1 F ( e j 2 π k M ) e j 2 π k m M = M 2 π ∑ n = − ∞ ∞ f [ n ] ∑ p = − ∞ ∞ δ [ m − n + p M ] = M 2 π ∑ p = − ∞ ∞ ∑ n = − ∞ ∞ f [ n ] δ [ m − n + p M ] = M 2 π ∑ p = − ∞ ∞ f [ m + p M ] . (4.12) \begin{aligned} g\left[ m \right] &= \frac{1}{{2\pi }}\sum\limits_{k = 0}^{M - 1} {F\left( {{e^{j\tfrac{{2\pi k}}{M}}}} \right){e^{j\tfrac{{2\pi km}}{M}}}} \\ &= \frac{M}{{2\pi }}\sum\limits_{n = - \infty }^\infty {f\left[ n \right]\sum\limits_{p = - \infty }^\infty {\delta \left[ {m - n + pM} \right]} } \\ &= \frac{M}{{2\pi }}\sum\limits_{p = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {f\left[ n \right]\delta \left[ {m - n + pM} \right]} } \\ &= \frac{M}{{2\pi }}\sum\limits_{p = - \infty }^\infty {f\left[ {m + pM} \right]} . \\ \end{aligned} \tag{4.12} g[m]=2π1k=0∑M−1F(ejM2πk)ejM2πkm=2πMn=−∞∑∞f[n]p=−∞∑∞δ[m−n+pM]=2πMp=−∞∑∞n=−∞∑∞f[n]δ[m−n+pM]=2πMp=−∞∑∞f[m+pM].(4.12)
这样我们就证明了,对序列 f [ n ] f\left[ n \right] f[n] 的离散时间傅里叶变换 F ( e j ω ) F\left( {{e^{j\omega }}} \right) F(ejω) 以 2 π / M 2\pi /M 2π/M 为间隔进行采样,会导致序列 f [ n ] f\left[ n \right] f[n] 以 M M M 为周期进行延拓与叠加,从而获得一个周期序列 g [ m ] g\left[ m \right] g[m]。因此, f [ n ] f\left[ n \right] f[n] 的有效长度与 M M M 的选择就成了我们需要讨论的对象。
在现实中我们所采集到的序列 f [ n ] f\left[ n \right] f[n] 的长度都是有限的,不妨记其为 N N N。由于 g [ m ] g\left[ m \right] g[m] 是 f [ n ] f\left[ n \right] f[n] 经过周期延拓与叠加的结果,当 N ⩽ M N \leqslant M N⩽M 时, f [ n ] f\left[ n \right] f[n] 的有效数据不会发生重叠,因此可以截取与缩放完整地从 g [ m ] g\left[ m \right] g[m] 中恢复;而当 N > M N > M N>M 时, f [ n ] f\left[ n \right] f[n] 部分有限数据发生重叠,因而不能从 g [ m ] g\left[ m \right] g[m] 中完整地恢复。我们之所以强调要从 g [ m ] g\left[ m \right] g[m] 中恢复 f [ n ] f\left[ n \right] f[n],是因为从式 (4.12) 中可知 g [ m ] g\left[ m \right] g[m] 可以通过有限项的求和运算求得,而无需任何积分运算,这对于计算机处理是至关重要的。总之,由于有限长序列 f [ n ] f\left[ n \right] f[n] 的长度 N N N 通常是已知的,不妨令 M = N M = N M=N 即可。综合式 (4.3) 与 (4.12),即可引出我们所要介绍的离散傅里叶变换。
对于一长度为 N N N 的有限长序列 f [ n ] f\left[ n \right] f[n],其中 n = 0 , 1 , . . . , N − 1 n = 0,1,...,N - 1 n=0,1,...,N−1,定义其 N N N 点离散傅里叶变换 (Discrete FT, DFT) 与反变换为
F [ k ] = F { f [ n ] } = ∑ n = 0 N − 1 f [ n ] e − j 2 π k n N , f [ n ] = F − 1 { F [ k ] } = 1 N ∑ k = 0 N − 1 F [ k ] e j 2 π k n N . (4.13) \begin{gathered} F\left[ k \right] = \mathcal{F}\left\{ {f\left[ n \right]} \right\} = \sum\limits_{n = 0}^{N - 1} {f\left[ n \right]{e^{ - j\tfrac{{2\pi kn}}{N}}}} , \\ f\left[ n \right] = {\mathcal{F}^{ - 1}}\left\{ {F\left[ k \right]} \right\} = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {F\left[ k \right]{e^{j\tfrac{{2\pi kn}}{N}}}} . \\ \end{gathered} \tag{4.13} F[k]=F{f[n]}=n=0∑N−1f[n]e−jN2πkn,f[n]=F−1{F[k]}=N1k=0∑N−1F[k]ejN2πkn.(4.13)
其证明可参考前述讨论,这里不再赘述。因为离散傅里叶变换的正变换与反变换都可以表示为有限项的求和运算,十分适合计算机与更广义的数字电路进行处理,所以其目前的应用非常广泛,不管是语音、图像还是股市、天气等各种数据的处理都可看见其身影。实际上,离散傅里叶变换更让人熟悉的名字是快速傅里叶变换 (Fast FT, FFT),两者内在原理是相同的,但是FFT利用DFT的性质,合并了部分运算,将 DFT 的运算复杂度从 O ( N 2 ) O\left( {{N^2}} \right) O(N2) 降至 O ( N log N ) O\left( {N\log N} \right) O(NlogN),而正是这种改进让 DFT 能够真正地在各种需要保证实时性的应用中变得实用。
5 总结
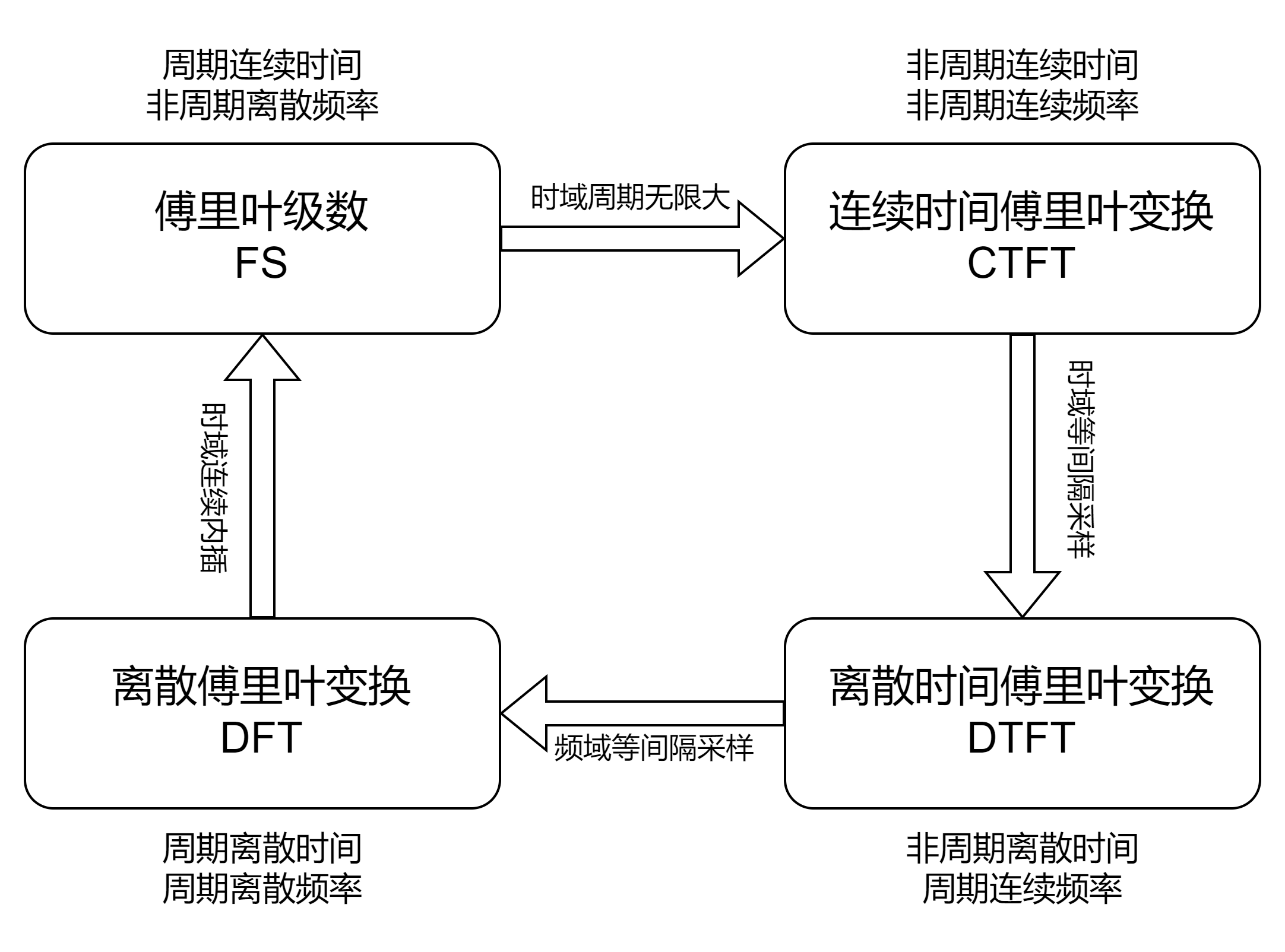
在前面的章节中,我们从上而下地讨论了傅里叶级数 (FS),连续时间傅里叶变换 (CTFT),离散时间傅里叶变换 (DTFT) 与离散傅里叶变换 (DFT)。从它们的名字也可以看出,这种区分主要在于从时域与频域周期性,以及时域与频域的连续性。为了更直观地看出它们的区别,这里做个简单的总结,四者关系如图 1 所示。
傅里叶级数 (FS):
定义:
F [ n ] = 1 T ∫ − T / 2 T / 2 f ( t ) e − j n ω 0 t d t , f ( t ) = ∑ n = − ∞ ∞ F n e j n ω 0 t . (5.1) \begin{gathered} F\left[ n \right] = \frac{1}{T}\int\limits_{ - T/2}^{T/2} {f\left( t \right){e^{ - jn{\omega _0}t}}dt} , \\ f\left( t \right) = \sum\limits_{n = - \infty }^\infty {{F_n}{e^{jn{\omega _0}t}}} . \\ \end{gathered} \tag{5.1} F[n]=T1−T/2∫T/2f(t)e−jnω0tdt,f(t)=n=−∞∑∞Fnejnω0t.(5.1)
其中 f ( t ) f\left( t \right) f(t) 为以 T = 2 π / ω 0 T = 2\pi /{\omega _0} T=2π/ω0 的周期连续时间函数, F [ n ] F\left[ n \right] F[n] 为离散序列。
连续时间傅里叶变换 (CTFT):
定义:
F ( j ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t f ( t ) = 1 2 π ∫ − ∞ ∞ F ( j ω ) e j ω t d ω . (5.2) \begin{gathered} F\left( {j\omega } \right) = \int\limits_{ - \infty }^\infty {f\left( t \right){e^{ - j\omega t}}dt} \\ f\left( t \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {F\left( {j\omega } \right){e^{j\omega t}}d\omega } . \\ \end{gathered} \tag{5.2} F(jω)=−∞∫∞f(t)e−jωtdtf(t)=2π1−∞∫∞F(jω)ejωtdω.(5.2)
其中 f ( t ) f\left( t \right) f(t)为非周期连续时间函数, F ( j ω ) F\left( {j\omega } \right) F(jω)为非周期连续频率函数。
离散时间傅里叶变换 (DTFT):
定义:
F ( e j ω ) = ∑ n = − ∞ ∞ f [ n ] e − j ω n . f [ n ] = 1 2 π ∫ − π π F ( e j ω ) e j ω n d ω . (5.3) \begin{gathered} F\left( {{e^{j\omega }}} \right) = \sum\limits_{n = - \infty }^\infty {f\left[ n \right]{e^{ - j\omega n}}} . \\ f\left[ n \right] = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {F\left( {{e^{j\omega }}} \right){e^{j\omega n}}d\omega } . \\ \end{gathered} \tag{5.3} F(ejω)=n=−∞∑∞f[n]e−jωn.f[n]=2π1−π∫πF(ejω)ejωndω.(5.3)
其中 f [ n ] f\left[ n \right] f[n] 为无限长离散序列, F ( e j ω ) F\left( {{e^{j\omega }}} \right) F(ejω) 为以 2 π 2\pi 2π 为周期的连续频率函数。
离散傅里叶变换 (DFT):
定义:
F [ k ] = ∑ n = 0 N − 1 f [ n ] e − j 2 π k n N , f [ n ] = 1 N ∑ k = 0 N − 1 F [ k ] e j 2 π k n N . (5.4) \begin{gathered} F\left[ k \right] = \sum\limits_{n = 0}^{N - 1} {f\left[ n \right]{e^{ - j\tfrac{{2\pi kn}}{N}}}} , \\ f\left[ n \right] = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {F\left[ k \right]{e^{j\tfrac{{2\pi kn}}{N}}}} . \\ \end{gathered} \tag{5.4} F[k]=n=0∑N−1f[n]e−jN2πkn,f[n]=N1k=0∑N−1F[k]ejN2πkn.(5.4)
其中 f [ n ] f\left[ n \right] f[n] 与 F [ k ] F\left[ k \right] F[k] 为长度为 N N N 的有限长离散序列,且两者可以 N N N 为周期进行周期延拓,改变求和区间不影响结果。
由于这四种变换都是在 e j x {e^{jx}} ejx 即复平面的单位圆上进行分析的,它们是否能够收敛需要满足狄利克雷条件,即绝对可积与绝对可和等,这通常是比较苛刻的。例如信号与系统中最常见的单位阶跃信号明显不满足绝对可积的条件,因此我们无法求得其傅里叶变换。为此,通过加入缩放项,我们可以选择在 e x + j y {e^{x + jy}} ex+jy 即复平面中不限大小的圆上进行讨论,从而引出了对连续时间信号的拉普拉斯变换与对离散时间信号的 z 变换,这两种变换能够提供更大的收敛域,从而能够分析更多类型的信号,包括前面所述的单位阶跃信号,它们是对线性移不变系统的稳定性与延时等性质分析的强有力工具。
实际上,对离散傅里叶变换进一步讨论还可以发展出很多非常实用的变换形式。例如,通过对有限长离散实数序列进行偶对称延拓,可以获得只包含实数余弦函数运算的离散余弦变换。同理,通过对有限长离散实数序列进行奇对称延拓,可以获得只包含实数正弦函数运算的离散正弦变换。另外,离散傅里叶变换主要适用于平稳信号,即信号的频谱分布不随时间而改变,然而不少场景下这种假设是不成立的,例如通信中的调频会使载波的频率随时间而改变,而人说话时声音中的频谱分布也会随着单词的改变而发生变化。除此以外,对于需要持续运行的系统,由于信号的长度是无限的,对信号整体的离散傅里叶变换分析也是不可能的。基于以上原因,我们又引出了短时傅里叶变换与小波变换,这两种变换对于非平稳信号的分析与处理十分有用。