本文介绍 openvins 中IMU仿真时基于控制轨迹和SPline插值，并计算IMU输出，的原理和代码。

参考

Open-vins中关于仿真的描述：https://docs.openvins.com/simulation.html
Open-vins论文：https://pgeneva.com/downloads/papers/Geneva2020ICRA.pdf
Open-vins所采用的SE3插值论文：https://link.springer.com/article/10.1007/s11263-015-0811-3
上述论文提到的BSpline的矩阵表示：https://xiaoxingchen.github.io/2020/03/02/bspline_in_so3/general_matrix_representation_for_bsplines.pdf

open-vins中的仿真部分结构

open-vins的文件目录中，如下文件与仿真有关：

ov_core/
	src/
		sim/
			BsplineSE3.cpp
			BsplineSE3.h
ov_msckf/
	src/
		sim/
			Simulator.cpp
			Simulator.h
		test_sim_meas.cpp
ov_data/
	sim/
		xxx.txt

其中，test_sim_meas.cpp 是仿真程序入口，调用的主函数为 Simualtor 类，openvins中所有的内容需要基于 ov_core 这个核心，具体的插值部分用的是 BsplineSE3 这个类。而载入的轨迹数据格式，可以参考 ov_data 路径的文件。

test_sim_meas.cpp
里面核心的函数是 get_next_imu(time_imu, wm, am)，其根据类内轨迹数据，计算再某一时刻的imu输出。

get_next_imu
位于 Simulator 类内，主要内容有两个：利用 Bspline 插值得到加速度和角速度， spline->get_acceleration；再添加随机游走和测量噪声。

get_acceleration
位于 BsplineSE3 类，主要内容包括：

1. 获取轨迹的控制点：find_bounding_control_points()
2. 计算 De Boor-Cox 矩阵系数
3. 轨迹插值，获得当前时刻的pose
4. 将pose转为加速度和角速度（世界系）
5. 将世界系的加速度和角速度，转到 IMU 系

针对1，只是把轨迹中当前时刻点的前后各2个pose拿出来，即pose0,1,2,3。当前需要插值的时刻是位于1和2之间。

原理解释

De Boor-Cox矩阵系数与轨迹插值

首先，openvins论文中给出的插值公式如下：
这个公式非常简略，看不出来在干什么。简单来说，就是为了计算 u(ts) 时刻得位姿 T，这个位姿是从S系转到G(世界)系的，那么此时需要用 (i-1)时刻的和$A_0,A_1,A_2$ 这4个矩阵计算。式(29)和(30)给出了$A$的表达式。

想要了解为什么这么算，就需要阅读参考文献[38]:
A Spline-Based Trajectory Representation for Sensor Fusion and Rolling Shutter Cameras

基于SE3的Bspline插值
这篇文章提出的动机是，多传感器融合时，不可能多个传感器完全在同一时刻获取数据，因此需要Bspline插值，因此提出了在SE3插值。

具体地，对于插值方法，有两种表示，分别是(1)和(2)，里面的$B$和$\tilde{B}$是两种不同表示的基，但本质上一样。这里采用的是第二种表示。

这种表示对于 SE3 的公式为：
这里的符号表示和openvins的不同，这里s表示插值时刻，w表示世界系。${\Omega }_i$ 就是上面的 $log(T_{w,i-1}^{-1},T_{w,i})$，和上一位姿间的 $se3$。

此时上述(3)式的变量只剩 ${\tilde{B}}_{0,k}(t)$，这个的计算方式由 Qin2000(General Matrix Representations for B-Splines) 这篇论文给出。这篇论文太复杂了看不懂，简单概括就是将BSpline用矩阵进行了表示。这里略过。

由于目标是为IMU提供数据，因此希望加速度是连续的，因此轨迹曲线采用C2连续(即二阶导连续)，C2连续只需要4个控制点，即前面2个后面2个，此时的矩阵是 4x4 的。上式的$u$即插值相对于上一控制点的增量。同时，这里给出了$\tilde{B}$的一阶导和二阶导。

接下来，论文给出了轨迹插值结果，以及插值的一阶导（速度）和二阶导（加速度）表达式。接下来的$A$就和openvins的一致了。

由pose计算IMU系得加速度与角速度

上面计算完，只是得到了轨迹相对于轨迹所在坐标系（即世界系）的轨迹、速度和加速度，接下来要求相对于IMU系。这个模型就比较简单：

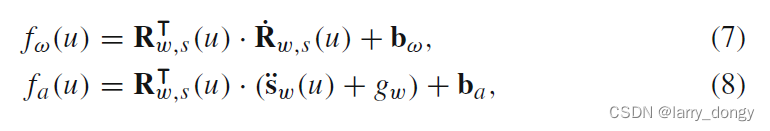
加速度，加上重力后，转到IMU系；
角速度，需要经过旋转矩阵求导，再转到IMU系。

代码与原理的对应

直接复制出来 openvins 中 BsplineSE3 中获取加速度和角速度的代码：

//~ 输入：待插值的时间戳；
/*~ 输出：IMU的加速度、角速度，以及一些姿态量；

~*/
bool BsplineSE3::get_acceleration(double timestamp, Eigen::Matrix3d &R_GtoI, Eigen::Vector3d &p_IinG, 
	Eigen::Vector3d &w_IinI, Eigen::Vector3d &v_IinG, Eigen::Vector3d &alpha_IinI, Eigen::Vector3d &a_IinG) {

  // Get the bounding poses for the desired timestamp
  double t0, t1, t2, t3;
  Eigen::Matrix4d pose0, pose1, pose2, pose3;
  bool success = find_bounding_control_points(timestamp, control_points, t0, pose0, t1, pose1, t2, pose2, t3, pose3);

  // Return failure if we can't get bounding poses
  if (!success) {
    alpha_IinI.setZero();
    a_IinG.setZero();
    return false;
  }
  //~ 这里就是计算上述B矩阵，B的一阶导，二阶导矩阵；
  // Our De Boor-Cox matrix scalars
  double DT = (t2 - t1);
  double u = (timestamp - t1) / DT;
  double b0 = 1.0 / 6.0 * (5 + 3 * u - 3 * u * u + u * u * u);
  double b1 = 1.0 / 6.0 * (1 + 3 * u + 3 * u * u - 2 * u * u * u);
  double b2 = 1.0 / 6.0 * (u * u * u);
  double b0dot = 1.0 / (6.0 * DT) * (3 - 6 * u + 3 * u * u);
  double b1dot = 1.0 / (6.0 * DT) * (3 + 6 * u - 6 * u * u);
  double b2dot = 1.0 / (6.0 * DT) * (3 * u * u);
  double b0dotdot = 1.0 / (6.0 * DT * DT) * (-6 + 6 * u);
  double b1dotdot = 1.0 / (6.0 * DT * DT) * (6 - 12 * u);
  double b2dotdot = 1.0 / (6.0 * DT * DT) * (6 * u);

  // Cache some values we use alot
  Eigen::Matrix<double, 6, 1> omega_10 = log_se3(Inv_se3(pose0) * pose1);
  Eigen::Matrix<double, 6, 1> omega_21 = log_se3(Inv_se3(pose1) * pose2);
  Eigen::Matrix<double, 6, 1> omega_32 = log_se3(Inv_se3(pose2) * pose3);
  Eigen::Matrix4d omega_10_hat = hat_se3(omega_10);
  Eigen::Matrix4d omega_21_hat = hat_se3(omega_21);
  Eigen::Matrix4d omega_32_hat = hat_se3(omega_32);

	// 这里计算了A0~A2，以及一阶导、二阶导
  // Calculate interpolated poses
  Eigen::Matrix4d A0 = exp_se3(b0 * omega_10);
  Eigen::Matrix4d A1 = exp_se3(b1 * omega_21);
  Eigen::Matrix4d A2 = exp_se3(b2 * omega_32);
  Eigen::Matrix4d A0dot = b0dot * omega_10_hat * A0;
  Eigen::Matrix4d A1dot = b1dot * omega_21_hat * A1;
  Eigen::Matrix4d A2dot = b2dot * omega_32_hat * A2;
  Eigen::Matrix4d A0dotdot = b0dot * omega_10_hat * A0dot + b0dotdot * omega_10_hat * A0;
  Eigen::Matrix4d A1dotdot = b1dot * omega_21_hat * A1dot + b1dotdot * omega_21_hat * A1;
  Eigen::Matrix4d A2dotdot = b2dot * omega_32_hat * A2dot + b2dotdot * omega_32_hat * A2;

  // Get the interpolated pose
  Eigen::Matrix4d pose_interp = pose0 * A0 * A1 * A2;
  R_GtoI = pose_interp.block(0, 0, 3, 3).transpose();
  p_IinG = pose_interp.block(0, 3, 3, 1);

  // Get the interpolated velocities
  // NOTE: Rdot = R*skew(omega) => R^T*Rdot = skew(omega) 
  //~ 式(5)，计算角速度插值，角速度转回IMU系
  Eigen::Matrix4d vel_interp = pose0 * (A0dot * A1 * A2 + A0 * A1dot * A2 + A0 * A1 * A2dot);
  w_IinI = vee(pose_interp.block(0, 0, 3, 3).transpose() * vel_interp.block(0, 0, 3, 3));
  v_IinG = vel_interp.block(0, 3, 3, 1);

  // Finally get the interpolated velocities
  // NOTE: Rdot = R*skew(omega)
  // NOTE: Rdotdot = Rdot*skew(omega) + R*skew(alpha) => R^T*(Rdotdot-Rdot*skew(omega))=skew(alpha)
  //~ 式(6)，计算速度插值，加速度转回IMU系
  Eigen::Matrix4d acc_interp = pose0 * (A0dotdot * A1 * A2 + A0 * A1dotdot * A2 + A0 * A1 * A2dotdot + 2 * A0dot * A1dot * A2 + 2 * A0 * A1dot * A2dot + 2 * A0dot * A1 * A2dot);   
  Eigen::Matrix3d omegaskew = pose_interp.block(0, 0, 3, 3).transpose() * vel_interp.block(0, 0, 3, 3);
  alpha_IinI = vee(pose_interp.block(0, 0, 3, 3).transpose() * (acc_interp.block(0, 0, 3, 3) - vel_interp.block(0, 0, 3, 3) * omegaskew));		
  a_IinG = acc_interp.block(0, 3, 3, 1);
  return true;
}