C++语法（18）---- set和map_哈里沃克的博客-CSDN博客https://blog.csdn.net/m0_63488627/article/details/130228232?spm=1001.2014.3001.5501

 目录

1.AVL树的概念

2.节点定义

3.AVL树的类实现

1.类定义

2.insert

1.全代码实现

2.思考角度

3.平衡因子的情况

4.调节平衡的旋转

3.Print

4.Check

1. 验证其为二叉搜索树

2. 验证其为平衡树

---

1.AVL树的概念

1.普通搜索二叉树的插入可能会出现退化变为单支树，这样查找的效率就变为了O(N)

2.AVL树是当插入新的节点时，保证每个节点的左右子树的高度差绝对值不超过1

3.AVL树的平衡实现是通过调整高度得到的

特征

1.左右子树也是AVL树

2.左右高度差绝对值(简称平衡因子，右子树高度-左子树高度)不超过1

2.节点定义

template<class K,class V>
struct AVLTreeNode
{
	pair<K,V> _kv;
	AVLTreeNode* _left;
	AVLTreeNode* _right;
	AVLTreeNode* _parent;
	int _bf;

	AVLTreeNode(const pair<K, V>& kv)
	:_kv(kv)
	, _left(nullptr)
	, _right(nullptr)
	, _parent(nullptr)
	, _bf(0)
	{}
};

1.搜索二叉树实现只传入让K,V直接当数据

2.AVL树中使用pair来进行合并K和V数据

3.节点为三叉节点，指向孩子和父亲节点

4._bf为平衡因子，这样直观表示是否平衡，根据因子进行调整

5.要记得初始化节点，这样下面实现才能用

3.AVL树的类实现

1.类定义

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
private:
	Node* _root = nullptr;
};

2.insert

1.先跟搜索二叉树的实现一样，插入到对应的位置

2.更新平衡因子

3.通过因子判断是否进行平衡调节 

1.全代码实现

bool Insert(const pair<K, V>& kv)
{
    //1.先跟搜索二叉树的实现一样，插入到对应的位置
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}

	//父子节点确定插入的位置
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
        //比cur要小，往cur的左边走
		if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
        //比cur要大，往cur的右边走
		else if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
        //相同，不插入
		else
			return false;
	}

    //走到这cur就是要插入的位置
	//cur要连接parent，parent也要连接cur---判断靠kv的大小

	cur = new Node(kv);
	if (parent->_kv.first > cur->_kv.first)
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_right = cur;
		cur->_parent = parent;
	}

    //2.更新平衡因子
	while (parent)
	{
		//左减右加
		if (parent->_left == cur)
		{
			parent->_bf--;
		}
		else if (parent->_right == cur)
		{
			parent->_bf++;
		}

	    //情况一_bf如果等于0，说明之前是 1/-1，说明现在加进去不会影响原来的平衡，退出就行
	    if (parent->_bf == 0)
		    break;

	    //如果等于1/-1，说明之前没有树，加进去就多一个高度 -- 判断祖先节点的_bf（通过循环）
	    else if (parent->_bf == 1 || parent->_bf == -1)
	    {
		    cur = parent;
			parent = parent->_parent;
		}
        //如果等于2/-2，说明这个节点下面要调整
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			//左旋
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				_RotateL(parent);
			}
			//右旋
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				_RotateR(parent);
			}
			//先左旋，再右旋
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				_RotateLR(parent);
			}
			else if (parent->_bf == 2 && cur->_bf == -1)
			{
				_RotateRL(parent);
			}
			else
			{
				assert(false);
			}
			break;
		}
		else
		{
			assert(false);
		}
	}
	return true;
}

2.思考角度

思想的前提：不要认为这个算法是用来使得已有搜索二叉树变平衡，而是加一个节点进行调节每一次加入该树都是平衡搜索二叉树。

3.平衡因子的情况

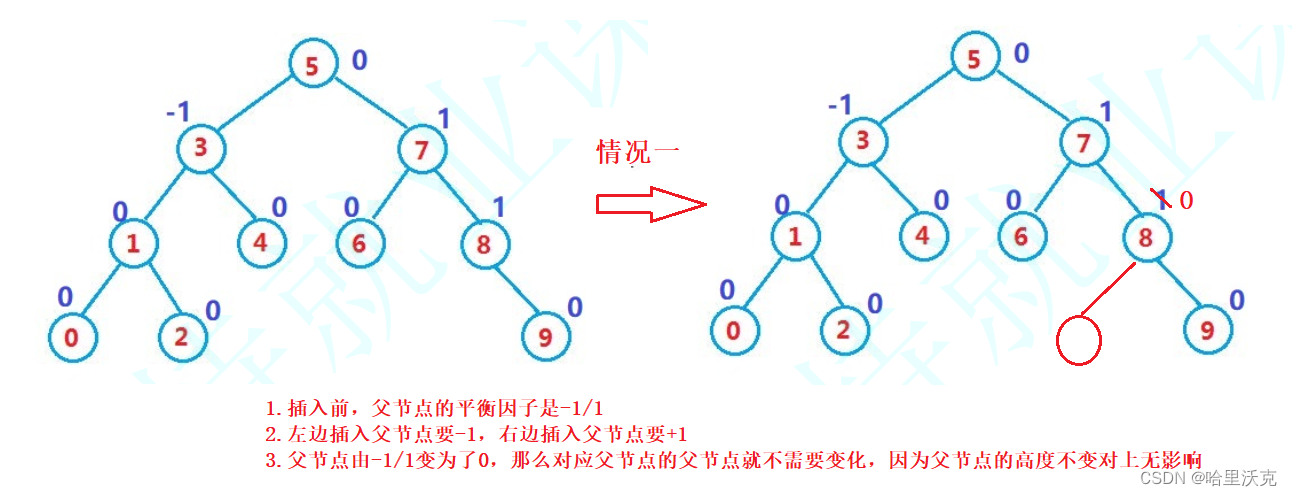
情况一子树的高度不变，上面的也不会影响

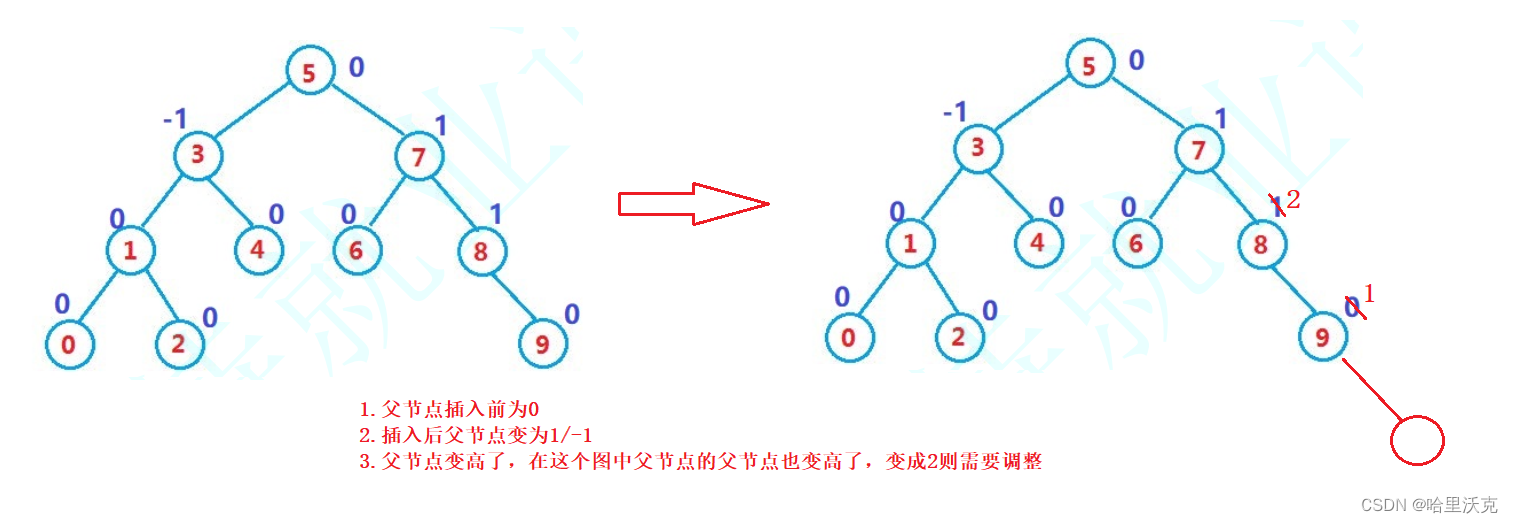
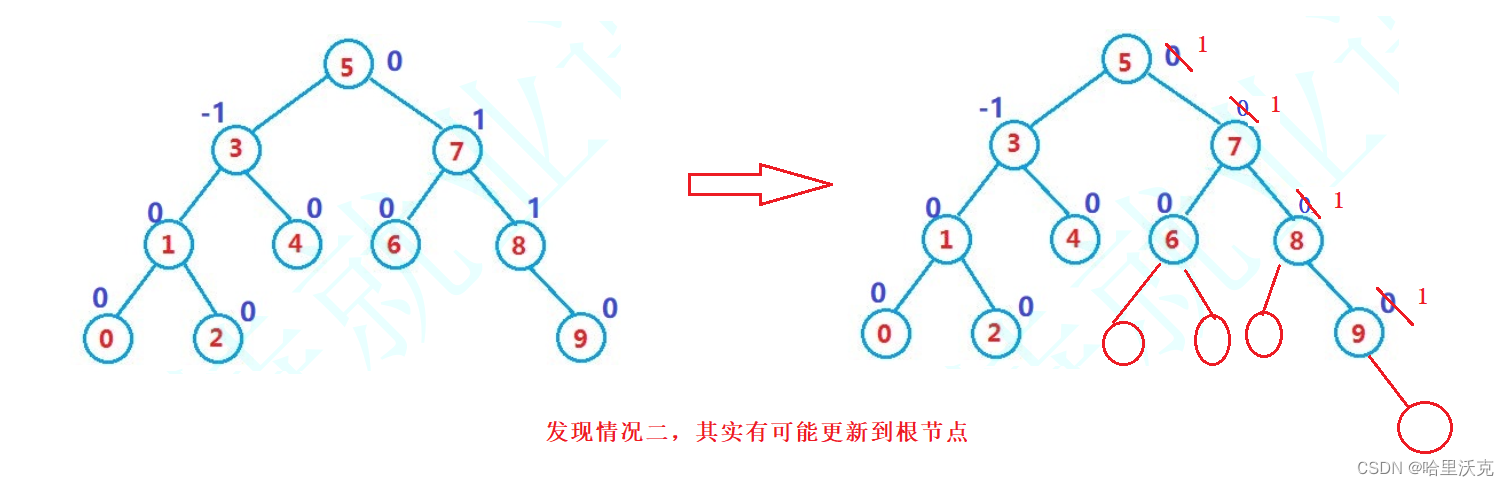
情况二可能会更新到跟节点，所以我们可能需要持续的更新，所以需要向上检测

4.调节平衡的旋转

1.旋转的目的

1.必须将这颗子树变成左右高度差绝对值不超过1

2.不允许其他位置的高度

3.更新平衡因子

4.降低子树的高度

2.旋转的情况

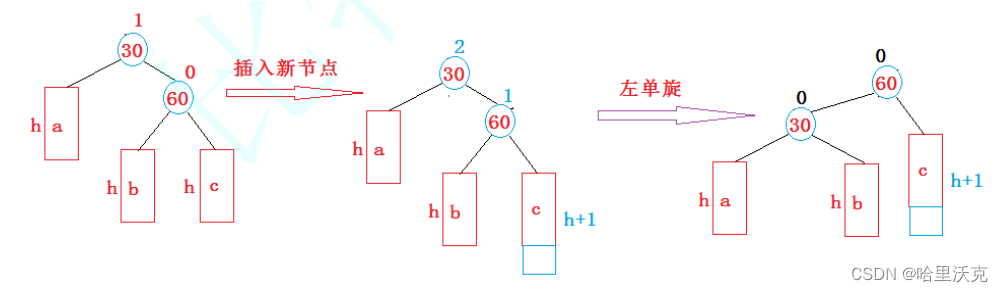
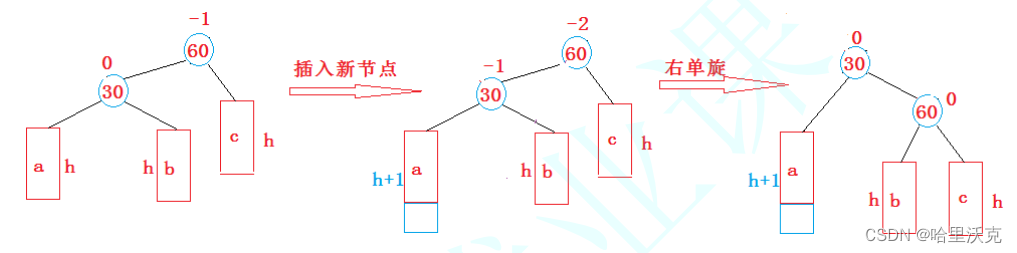
1.左单旋

60右边变成30左边，60左边变成30；60和30的平衡因子变为0

void _RotateL(Node*& parent)
{
	Node* pparent = parent->_parent;
	Node* SubR = parent->_right;
	Node* SubRL = SubR->_left;
	if (pparent == nullptr)
	{
		_root = SubR;
		SubR->_parent = nullptr;
	}
	else
	{
		if (pparent->_left == parent)
			pparent->_left = SubR;
		else
			pparent->_right = SubR;
		SubR->_parent = pparent;
	}
	parent->_parent = SubR;
	SubR->_left = parent;
	parent->_right = SubRL;
	if (SubRL != nullptr)
		SubRL->_parent = parent;
	parent->_bf = 0;
	SubR->_bf = 0;
}

2.右单旋

void _RotateR(Node*& parent)
{
	Node* pparent = parent->_parent;
	Node* SubL = parent->_left;
	Node* SubLR = SubL->_right;
	if (pparent == nullptr)
	{
		_root = SubL;
		SubL->_parent = nullptr;
	}
	else
	{
		if (pparent->_left == parent)
			pparent->_left = SubL;
		else
			pparent->_right = SubL;
		SubL->_parent = pparent;
	}
	parent->_parent = SubL;
	SubL->_right = parent;
	parent->_left = SubLR;
	if (SubLR != nullptr)
		SubLR->_parent = parent;
	parent->_bf = 0;
	SubL->_bf = 0;
}

 3.先右单旋再左单旋

虽说右单旋再左单旋就完成了对应的结构，但这些节点的平衡因子是被打乱的；

从结果上看，其实就是将最60的左右子树平分给它父节点和“爷爷”节点

60的平衡因子不管怎么样都是0是确定的

但是另外两个节点平衡因子是看原先60的平衡因子：

b为h的话，30平衡因子为0，90的平衡因子为1

c为h的话，30平衡因子为-1，90的平衡因子为0

因此，我们需要一个临时平衡因子tmp_bf存储60位置的平衡因子

60是新增节点，那么30和90的平衡因子都是0了

60的子数是新增，那需要看这个临时因子

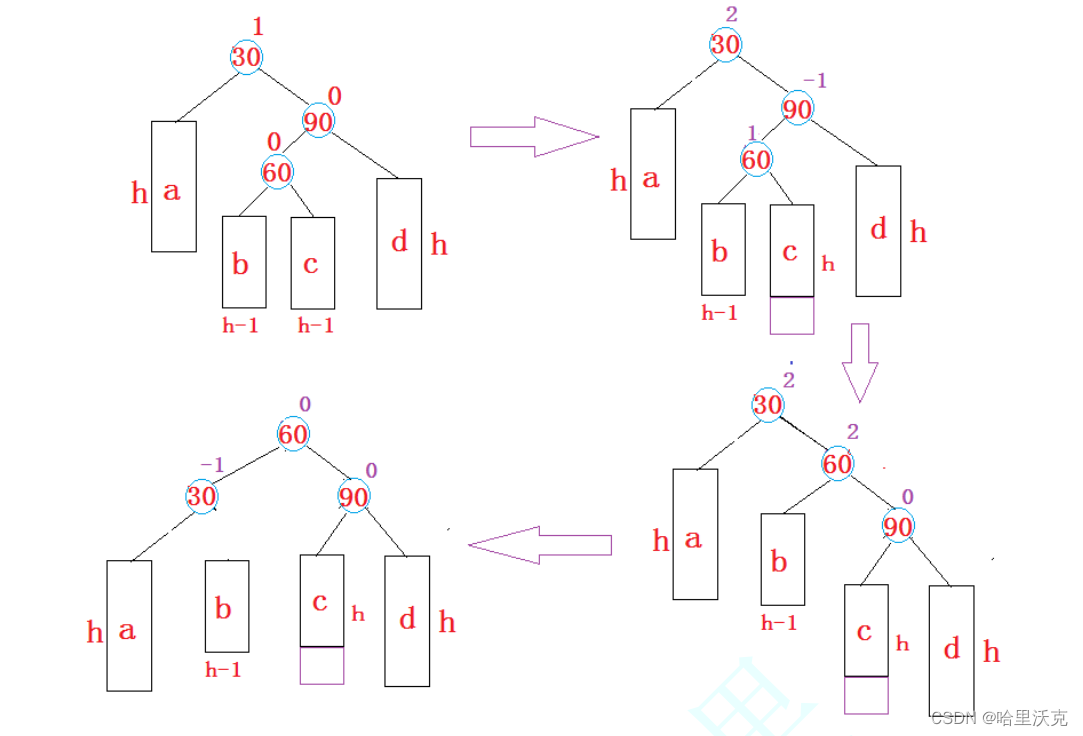
void _RotateRL(Node*& parent)
{
	Node* SubR = parent->_right;
	Node* SubRL = SubR->_left;
	int tmp_bf = 0;
	 if (SubRL->_left == nullptr && SubRL->_right == nullptr)
		tmp_bf = 0;
	else
		tmp_bf = SubRL->_bf;
	_RotateR(SubR);
	_RotateL(parent);
	if (tmp_bf == 0)
		parent->_bf = SubRL->_bf = 0;
	else if (tmp_bf == -1)
	{
		parent->_bf = 0;
		SubR->_bf = 1;
	}
	else
	{
		parent->_bf = -1;
    	SubR->_bf = 0;
	}
	SubRL->_bf = 0;
}

4.先左单旋再右单旋

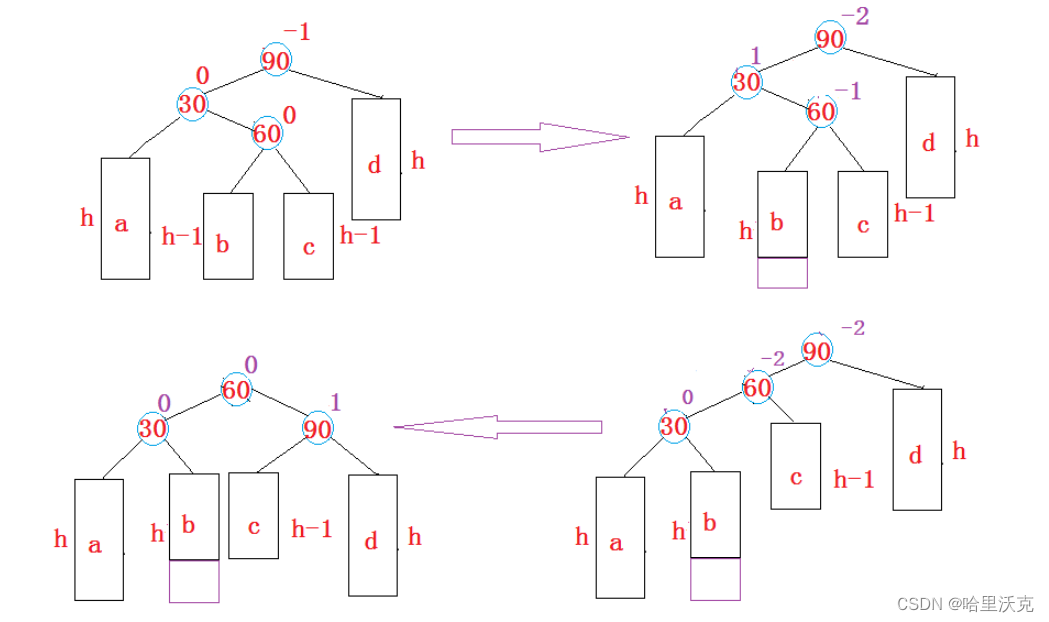
void _RotateLR(Node*& parent)
{
	Node* SubL = parent->_left;
	Node* SubLR = SubL->_right;
	int tmp_bf = 0;
	if (SubLR->_left == nullptr && SubLR->_right == nullptr)
		tmp_bf = 0;
	else
		tmp_bf = SubLR->_bf;
	_RotateL(SubL);
	_RotateR(parent);
	if (tmp_bf == 0)
		parent->_bf = SubLR->_bf = 0;
	else if(tmp_bf == -1)
	{
		parent->_bf = 1;
		SubL->_bf = 0;
	}
	else
	{
		parent->_bf = 0;
		SubL->_bf = -1;
	}
	SubLR->_bf = 0;
}

3.Print

搜索二叉树顺序打印是通过中序遍历得到的

void Print()
{
	_Print(_root);
}

private:
void _Print(Node*& cur)
{
	if (cur == nullptr)
		return;
	_Print(cur->_left);
	cout << cur->_kv.first << endl;
	_Print(cur->_right);
}

4.Check

1. 验证其为二叉搜索树

如果中序遍历可得到一个有序的序列，就说明为二叉搜索树

2. 验证其为平衡树

每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
节点的平衡因子是否计算正确

bool Check()
{
	return _Check(_root, 0);
}

private:
int Height(Node* root)
{
	if (root == nullptr)
		return 0;
	int Left = 1 + Height(root->_left);
	int Right = 1 + Height(root->_right);

	return (Left > Right ? Left : Right);
}

bool _Check(Node* root,int num)
{
	if (root == nullptr)
		return true;

	int leftHeight = Height(root->_left);
	int rightHeight = Height(root->_right);
    int diff = rightHeight - leftHeight;
	if (diff != root->_bf)
	{
		cout << "_bf false";
		return false;
	}
	if (diff < -1 || diff > 1)
	{
		cout << "diff false";
		return false;
	}

	return _Check(root->_left, leftHeight) && _Check(root->_right, rightHeight);
}