---

前言

---

此篇为动态规划的初阶篇，所以比较简单，适合刚入门的新手学，如果你已经入门了，就无需看这了，以后我会持续更新关于动态规划的文章的

一、斐波那契数

1.题目介绍

509. 斐波那契数

2.思路

1.确定初始状态

f[0]=0，f[1]=1；

2. 确定状态

我们所需要求的是f[n]

2.确定状态转移方程

f[n]是由从f[n-1]和f[n-2]转换来的

3.代码

int fib(int n){
   int f[35];
   f[0]=0;
   f[1]=1;
   for(int i=2;i<=n;i++)
   {
       f[i]=f[i-1]+f[i-2];
   }
   return f[n];
}

二、爬楼梯

1.题目介绍

爬楼梯

2.思路

其实与上面的斐波那契数的题是差不多的，就是需要改变以下思维
设f[n]为到达n层所有的方法
1.确定初始状态

从0层到一层，只能跨一步到第一层，即f[1]=1，从0层到第二层可以跨两个一步或者直接跨2步到第二层，即f[2]=2；

2. 确定状态

我们所需要求的是f[n]

2.确定状态转移方程

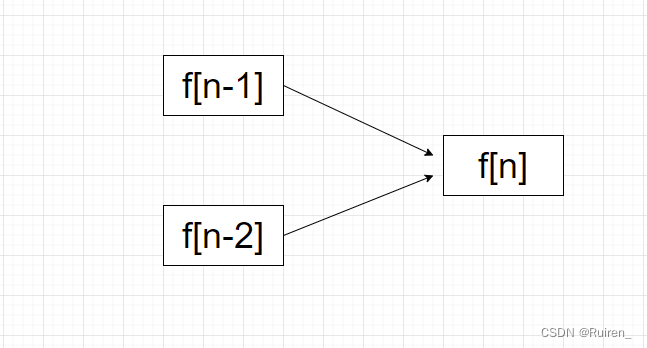
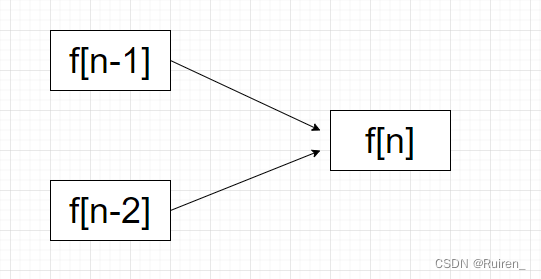
要想到达f[n]，有两种方法可以到达，从f[n-1]向上跨一步或者从f[n-2]向上跨两步，所以到达f[n]的方法是到f[n-1]和到f[n-2]的方法的和

3.代码

int climbStairs(int n){
        int f[50]={0};
        f[1]=1;
        f[2]=2;
        for(int i=3;i<=n;i++)
        {
            f[i]=f[i-1]+f[i-2];
        }
        return f[n];
}

三、使用最小花费爬楼梯

1.题目介绍

使用最小花费爬楼梯

2.思路

此题与上题很相似，但此题不是求方法，而是求最低的花费，同样只需要将思维转换一下就行了
设f[n]为到达n层的最低花费
1.确定初始状态

本题说可以从0层和一层开始，但是要想最低花费，肯定从1层开始嘛，所以f[0]=0；
初始在0层，所以f[1]=0；

2. 确定状态

我们所需要求的是f[n]

2.确定状态转移方程

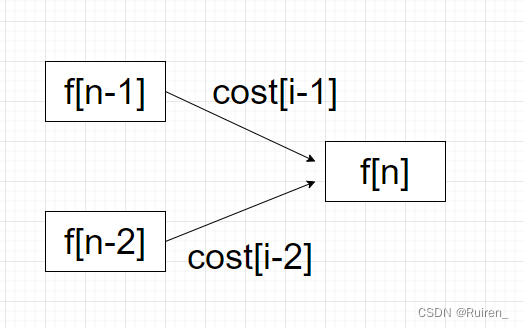
要想到达f[n]花费最小，有两种方法可以到达，所以有两种花费，比较f[n-1]向上跨一步加上跨一步的花费和从f[n-2]向上跨两步加上跨两步的花费，去最低者，即使f[n]的最低花费

3.代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
     int f[10000]={0};
     f[0]=0;
     f[1]=0;
     int size=cost.size();
     for(int i=2;i<=size;i++)
     {
         f[i]=min(f[i-1]+cost[i-1],f[i-2]+cost[i-2]);
     }
     
    return f[size];
    }
};