注意力机制里面的非参数注意力汇聚

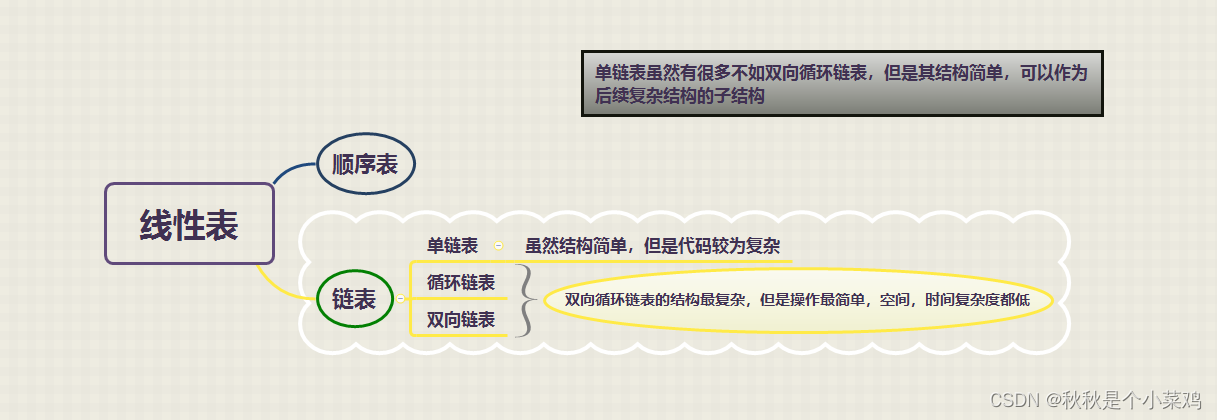
目录

1.目标任务

2.数据生成

2.1构造原始数值

3.非参数注意力汇聚

4.对注意力机制的理解

---

1.目标任务

使用y_train(有噪声),拟合y_truth(没噪声)。给你所有的y_train，构造注意力权重生成拟合曲线。

2.数据生成

n_train = 50 # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5) # 排序后的训练样本

其中：对于sort的返回值：

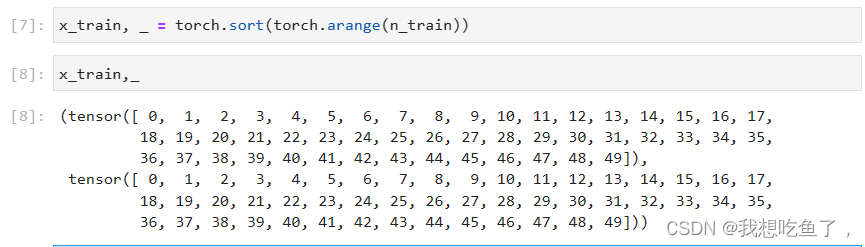
 sort返回两个值，第一个是拍好了从小到大的顺序后的values，另一个是对应原数据的indices

2.1构造原始数值

噪声服从u=0;std=0.5的正态分布：

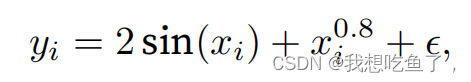
 y_train为上述计算式，包含噪声；y_truth为上式不包含噪声

def f(x):
    return 2 * torch.sin(x) + x**0.8

y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,)) # 训练样本的输出
x_test = torch.arange(0, 5, 0.1) # 测试样本
y_truth = f(x_test) # 测试样本的真实输出
n_test = len(x_test) # 测试样本数
n_test

训练样本是有噪声的x_train与y_train;真实数据是不带噪声的y_truth

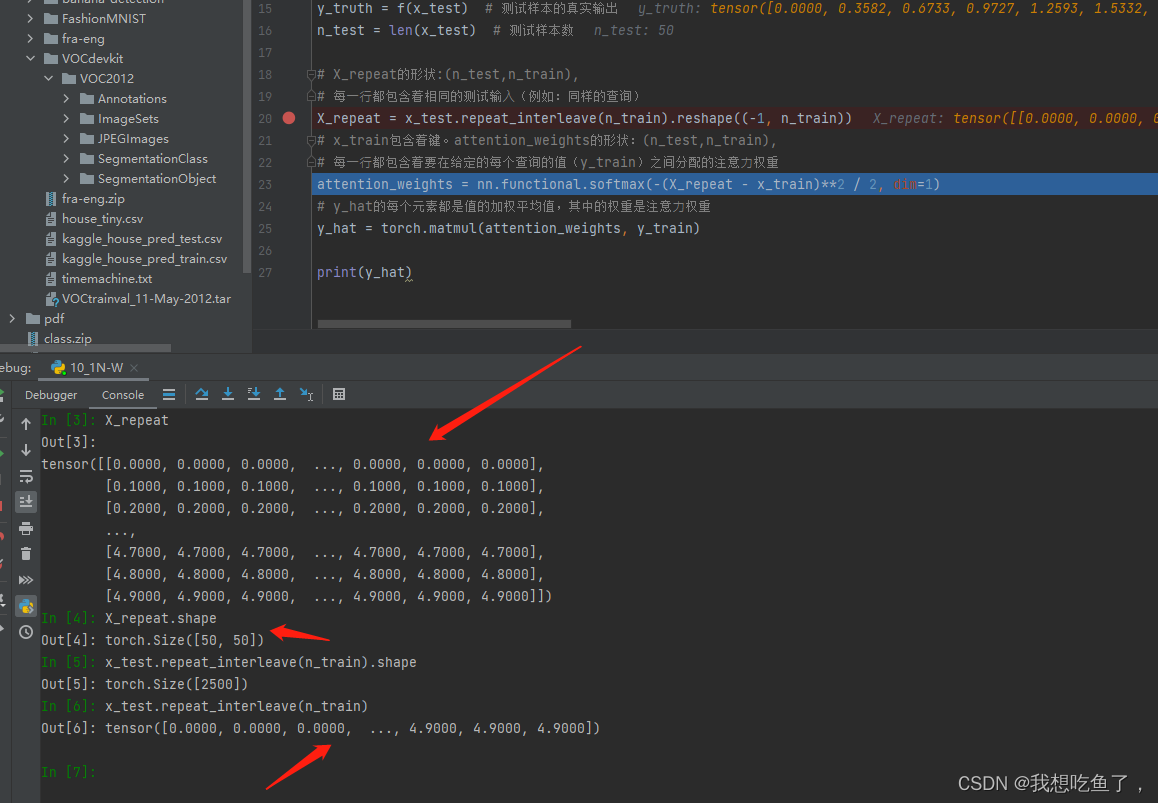
3.非参数注意力汇聚

# X_repeat的形状:(n_test,n_train),
# 每⼀⾏都包含着相同的测试输⼊（例如：同样的查询）
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))
# x_train包含着键。attention_weights的形状：(n_test,n_train),
# 每⼀⾏都包含着要在给定的每个查询的值（y_train）之间分配的注意⼒权重
attention_weights = nn.functional.softmax(-(X_repeat - x_train)**2 / 2, dim=1)
# y_hat的每个元素都是值的加权平均值，其中的权重是注意⼒权重
y_hat = torch.matmul(attention_weights, y_train)
plot_kernel_reg(y_hat)

上块代码中：

repeat_interleave就是将原来的x_test中的每一个元素赋值n_train次，得到一个一维tensor，再使用reshape操作使复制的相同元素都在同一行中。

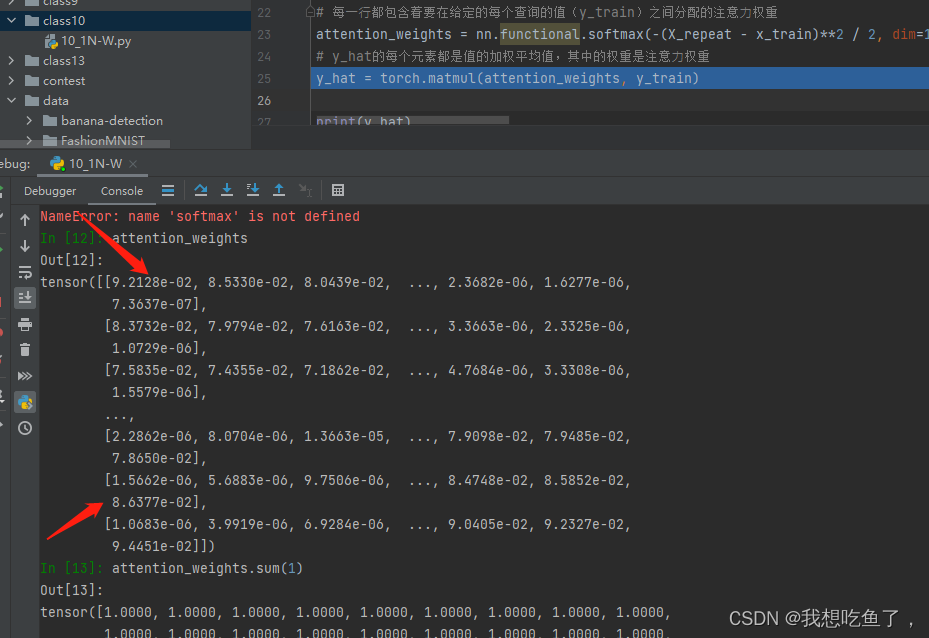
 对dim=1进行softmax，即将每个Xi与给定x的距离首先进行:1.映射非负(exp)+2.归一化。此时attention_weights表示各个候选Xi与给定x的距离的归一化权重。

 

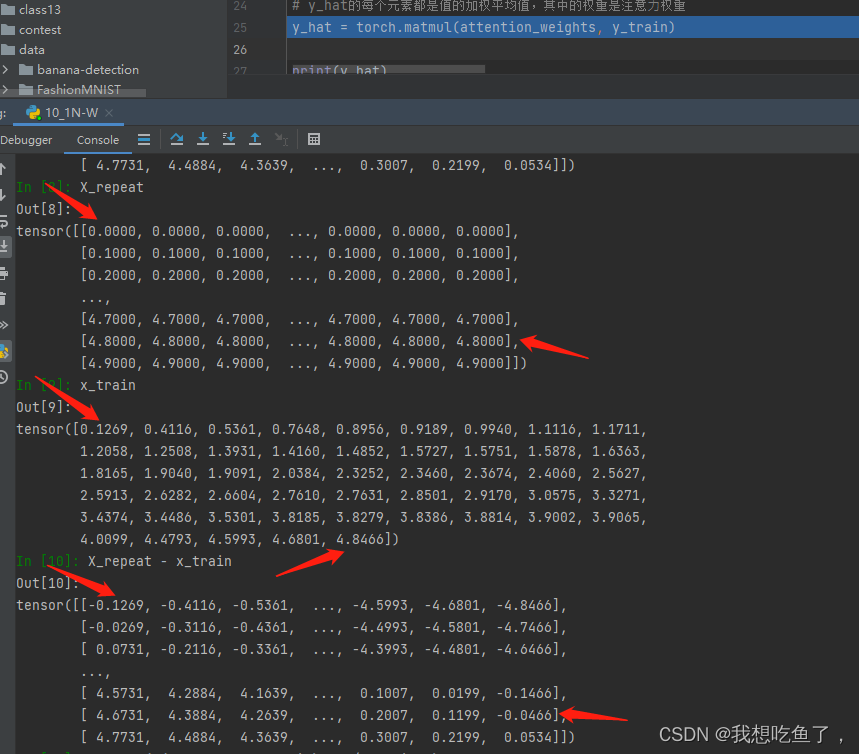
 由图可见，在第一行给定的x=0,距离Xi中对应的X1距离最近，其余该行上的值绝对值都比它大，所以最后的softmax它得分最多，权重最多；对于倒数第二行对应的x=4.8，最后一个X50=4.8466距离最近，所以对应位置的softmax得分最高

X_repeat - x_train，形状为(50,50)-(50)，第一个tensor中的每一行的各个元素减去第二个tensor里面的每个元素，用来计算给定x(0.1等分)与候选Xi的距离

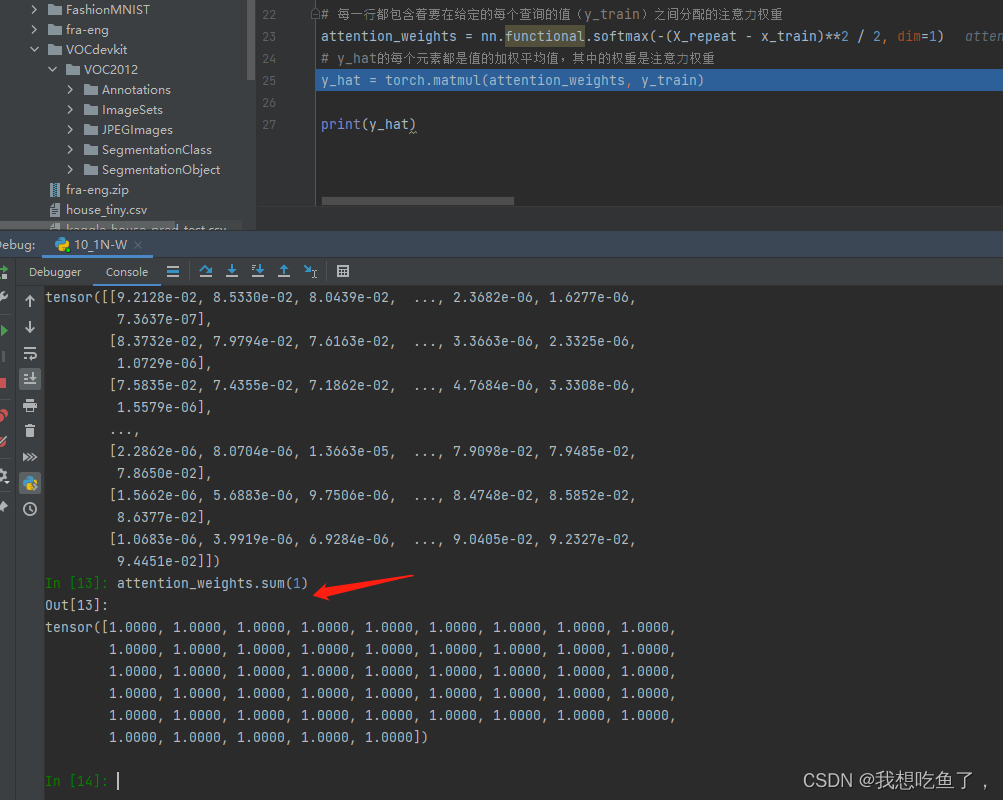
 dim=1表示的是沿着列增的方向操作，本质是对每一行操作！！！

4.对注意力机制的理解

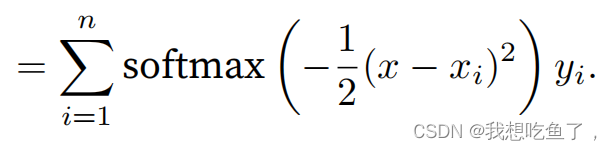
 给定x时(0.1等距分布),对所有候选Xi（rand)计算一下与x的距离(得到的X_repeat - x_train是(50,50)的tensor，其中每一行表示单个指定的x与各个Xi的距离。

  任务的目的使用y_train(有噪声),拟合y_truth(没噪声)。给你所有的y_train，构造权重生成拟合曲线。

  至于具体的在某个拟合点x(0.1等分)，用attention_weights与所有的y_train相乘，每一行表示的是各个x_train(候选Xi)与x的距离的softmax值，距离越近权重越大，考虑的就越多。