L2-013 红色警报
战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序,当失去一个城市导致国家被分裂为多个无法连通的区域时,就发出红色警报。注意:若该国本来就不完全连通,是分裂的k个区域,而失去一个城市并不改变其他城市之间的连通性,则不要发出警报。
Input
输入在第一行给出两个整数N(0 < N ≤ 500)和M(≤ 5000),分别为城市个数(于是默认城市从0到N-1编号)和连接两城市的通路条数。随后M行,每行给出一条通路所连接的两个城市的编号,其间以1个空格分隔。在城市信息之后给出被攻占的信息,即一个正整数K和随后的K个被攻占的城市的编号。
注意:输入保证给出的被攻占的城市编号都是合法的且无重复,但并不保证给出的通路没有重复。
Output
对每个被攻占的城市,如果它会改变整个国家的连通性,则输出Red Alert: City k is lost!,其中k是该城市的编号;否则只输出City k is lost.即可。如果该国失去了最后一个城市,则增加一行输出Game Over.。
思路:一眼数连通块,那就是DFS搜一下,判断是否是断点,就是当前连通块数-前一个状态连通块数>=2。因为断开这个点后,容易得知连通块多了1,它本身也是一个连通块,所以多了2。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 505;
int n, m, k;
int mp[N][N];
bool vis[N];
void DFS(int u) {
vis[u] = true;
for(int i = 0; i < n; i ++) {
if(mp[u][i] && !vis[i])
DFS(i);
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n >> m;
while(m --) {
int u, v;
std::cin >> u >> v;
mp[u][v] = mp[v][u] = 1;
}
int num = 0;
for(int i = 0; i < n; i ++) {
if(!vis[i])
num ++, DFS(i);
}
std::cin >> k;
for(int i = 1; i <= k; i ++) {
int x;
std::cin >> x;
for(int j = 0; j < n; j ++) {
if(mp[j][x])
mp[j][x] = mp[x][j] = 0;
}
memset(vis, 0, sizeof(vis));
int cnt = 0;
for(int j = 0; j < n; j ++) {
if(!vis[j])
cnt ++, DFS(j);
}
if(cnt - num >= 2)
std::cout << "Red Alert: City " << x << " is lost!" << '\n';
else
std::cout << "City " << x << " is lost." << '\n';
num = cnt;
}
if(k >= n)
std::cout << "Game Over." << '\n';
return 0;
}L2-014 列车调度
火车站的列车调度铁轨的结构如下图所示。
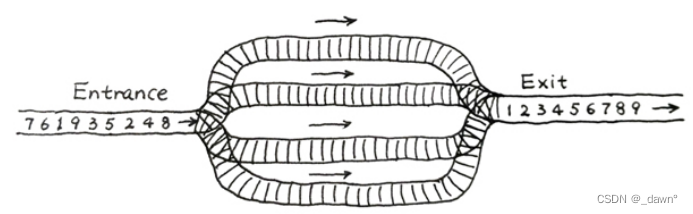
两端分别是一条入口(Entrance)轨道和一条出口(Exit)轨道,它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入,最后从出口离开。在图中有9趟列车,在入口处按照{8,4,2,5,3,9,1,6,7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开,则至少需要多少条平行铁轨用于调度?
Input
输入第一行给出一个整数N (2 ≤ N ≤10^5),下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。
Output
在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。
思路:显然与LIS问题相关,意思是找到最长上升子序列最少有多少。可以用set科技解决,也可以数组模拟upper_bound解决。每次遇到一个数找到大于该数的最小值,修改这个数的值,否则就再向数组中加入一个数。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int n, x, cnt;
int a[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n;
for(int i = 1; i <= n; i ++) {
std::cin >> x;
if(!cnt) a[++ cnt] = x;
else {
int pos = std::upper_bound(a + 1, a + 1 + cnt, x) - a;
if(a[pos] > x)
a[pos] = x;
else
a[++ cnt] = x;
}
}
std::cout << cnt << '\n';
return 0;
}L2-015 互评成绩
学生互评作业的简单规则是这样定的:每个人的作业会被k个同学评审,得到k个成绩。系统需要去掉一个最高分和一个最低分,将剩下的分数取平均,就得到这个学生的最后成绩。本题就要求你编写这个互评系统的算分模块。
Input
输入第一行给出3个正整数N(3 < N ≤10^4,学生总数)、k(3 ≤ k ≤ 10,每份作业的评审数)、M(≤ 20,需要输出的学生数)。随后N行,每行给出一份作业得到的k个评审成绩(在区间[0, 100]内),其间以空格分隔。
Output
按非递减顺序输出最后得分最高的M个成绩,保留小数点后3位。分数间有1个空格,行首尾不得有多余空格。
思路:模拟。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e4 + 5;
int n, k, m;
int a[N];
double ans[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n >> k >> m;
for(int i = 1; i <= n; i ++) {
double sum = 0;
for(int j = 1; j <= k; j ++) {
std::cin >> a[j];
sum += a[j];
}
std::sort(a + 1, a + 1 + k);
sum -= (a[1] + a[k]);
ans[i] = sum / (k - 2);
}
std::sort(ans + 1, ans + 1 + n);
m = std::min(m, n);
std::cout << std::fixed << std::setprecision(3);
for(int i = n - m + 1; i <= n; i ++) {
std::cout << ans[i] << " \n"[i == n];
}
return 0;
}L2-016 愿天下有情人都是失散多年的兄妹
呵呵。大家都知道五服以内不得通婚,即两个人最近的共同祖先如果在五代以内(即本人、父母、祖父母、曾祖父母、高祖父母)则不可通婚。本题就请你帮助一对有情人判断一下,他们究竟是否可以成婚?
Input
输入第一行给出一个正整数N(2 ≤ N ≤104),随后N行,每行按以下格式给出一个人的信息:
本人ID 性别 父亲ID 母亲ID
其中ID是5位数字,每人不同;性别M代表男性、F代表女性。如果某人的父亲或母亲已经不可考,则相应的ID位置上标记为-1。
接下来给出一个正整数K,随后K行,每行给出一对有情人的ID,其间以空格分隔。
注意:题目保证两个人是同辈,每人只有一个性别,并且血缘关系网中没有乱伦或隔辈成婚的情况。
Output
对每一对有情人,判断他们的关系是否可以通婚:如果两人是同性,输出Never Mind;如果是异性并且关系出了五服,输出Yes;如果异性关系未出五服,输出No。
思路:保存每个编号的父母关系,以及每个编号的性别,直接对于询问的两人DFS两遍,看看有没有重复访问的点。注意一个很坑的地方,父母编号给出时,父母的性别也是给定的,这是需要保存的信息!
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int n, q;
bool vis[N], flag, viss[N];
struct node {
int f, m, s;
} e[N];
void DFS1(int u, int cnt) {
if(cnt > 4) return;
if(e[u].f != -1 && !vis[e[u].f]) {
vis[e[u].f] = true;
DFS1(e[u].f, cnt + 1);
}
if(e[u].m != -1 && !vis[e[u].m]) {
vis[e[u].m] = true;
DFS1(e[u].m, cnt + 1);
}
}
void DFS2(int u, int cnt) {
if(cnt > 4) return;
if(e[u].f != -1 && vis[e[u].f]) {
flag = false;
return;
}
if(e[u].m != -1 && vis[e[u].m]) {
flag = false;
return;
}
if(e[u].f != -1 && !viss[e[u].f]) {
viss[e[u].f] = true;
DFS2(e[u].f, cnt + 1);
}
if(e[u].m != -1 && !viss[e[u].m]) {
viss[e[u].m] = true;
DFS2(e[u].m, cnt + 1);
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n;
for(int i = 1; i <= N; i ++) {
e[i] = {-1, -1, -1};
}
for(int i = 1; i <= n; i ++) {
int id, f, m;
char s;
std::cin >> id >> s >> f >> m;
if(f != -1) e[f].s = 1;
if(m != -1) e[m].s = 0;
e[id].f = f, e[id].m = m, e[id].s = (s == 'F' ? 0 : 1);
}
std::cin >> q;
while(q --) {
int x, y;
flag = true;
std::cin >> x >> y;
memset(vis, 0, sizeof(vis));
memset(viss, 0, sizeof(viss));
DFS1(x, 1);
DFS2(y, 1);
if(e[x].s == e[y].s)
std::cout << "Never Mind" << '\n';
else if(flag)
std::cout << "Yes" << '\n';
else
std::cout << "No" << '\n';
}
return 0;
}L2-017 人以群分
社交网络中我们给每个人定义了一个“活跃度”,现希望根据这个指标把人群分为两大类,即外向型(outgoing,即活跃度高的)和内向型(introverted,即活跃度低的)。要求两类人群的规模尽可能接近,而他们的总活跃度差距尽可能拉开。
Input
输入第一行给出一个正整数N(2≤N≤105)。随后一行给出N个正整数,分别是每个人的活跃度,其间以空格分隔。题目保证这些数字以及它们的和都不会超过2^31。
Output
按下列格式输出:
Outgoing #: N1
Introverted #: N2
Diff = N3
其中N1是外向型人的个数;N2是内向型人的个数;N3是两群人总活跃度之差的绝对值。
思路:如果是偶数个人,则直接排序后中间分开;若是奇数个人,比较前后哪个是n/2时差较大。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int n;
ll a[N], pre[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n;
for(int i = 1; i <= n; i ++) {
std::cin >> a[i];
}
std::sort(a + 1, a + 1 + n);
for(int i = 1; i <= n; i ++) {
pre[i] = pre[i - 1] + a[i];
}
int cnt1 = n / 2, cnt2 = n - cnt1;
ll dif = pre[n] - pre[cnt1] - pre[cnt1];
if(n & 1) {
if(dif < pre[n] - pre[cnt1 + 1] - pre[cnt1 + 1])
cnt1 ++, cnt2 --, dif = pre[n] - pre[cnt1 + 1] - pre[cnt1 + 1];
}
std::cout << "Outgoing #: " << cnt2 << '\n';
std::cout << "Introverted #: " << cnt1 << '\n';
std::cout << "Diff = " << abs(dif) << '\n';
return 0;
}L2-018 多项式A除以B
这仍然是一道关于A/B的题,只不过A和B都换成了多项式。你需要计算两个多项式相除的商Q和余R,其中R的阶数必须小于B的阶数。
Input
输入分两行,每行给出一个非零多项式,先给出A,再给出B。每行的格式如下:
N e[1] c[1] ... e[N] c[N]
其中N是该多项式非零项的个数,e[i]是第i个非零项的指数,c[i]是第i个非零项的系数。各项按照指数递减的顺序给出,保证所有指数是各不相同的非负整数,所有系数是非零整数,所有整数在整型范围内。
Output
分两行先后输出商和余,输出格式与输入格式相同,输出的系数保留小数点后1位。同行数字间以1个空格分隔,行首尾不得有多余空格。注意:零多项式是一个特殊多项式,对应输出为0 0 0.0。但非零多项式不能输出零系数(包括舍入后为0.0)的项。在样例中,余多项式其实有常数项-1/27,但因其舍入后为0.0,故不输出。
思路:用两个数组分别存储两个多项式,另一个数组存商,循环相除求解,细节见代码。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int a, b, x;
double y;
double c1[N], c2[N], c3[N];
int f(double a[], int e) {
int cnt = 0;
for(int i = e; i >= 0; i --) {
if(fabs(a[i]) > 0.05)
cnt ++;
}
return cnt;
}
void solve(double a[], int e) {
std::cout << f(a, e);
if(!f(a, e)) {
std::cout << " 0 0.0" << '\n';
return;
}
for(int i = e; i >= 0; i --) {
if(fabs(a[i]) > 0.05)
std::cout << ' ' << i << ' ' << std::fixed << std::setprecision(1) << a[i];
}
std::cout << '\n';
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> a;
int max1, max2;
for(int i = 1; i <= a; i ++) {
std::cin >> x >> y;
if(i == 1)
max1 = x;
c1[x] = y;
}
std::cin >> b;
for(int i = 1; i <= b; i ++) {
std::cin >> x >> y;
if(i == 1)
max2 = x;
c2[x] = y;
}
int d = max1 - max2;
while(max1 >= max2) {
double v = c1[max1] / c2[max2];
c3[max1 - max2] = v;
for(int i = max1, j = max2; i >= 0 && j >= 0; i --, j --) {
c1[i] -= v * c2[j];
}
if(fabs(c1[max1]) < 0.05) max1 --;
}
solve(c3, d);
solve(c1, max1);
return 0;
}L2-019 悄悄关注
新浪微博上有个“悄悄关注”,一个用户悄悄关注的人,不出现在这个用户的关注列表上,但系统会推送其悄悄关注的人发表的微博给该用户。现在我们来做一回网络侦探,根据某人的关注列表和其对其他用户的点赞情况,扒出有可能被其悄悄关注的人。
Input
输入首先在第一行给出某用户的关注列表,格式如下:
人数N 用户1 用户2 …… 用户N
其中N是不超过5000的正整数,每个用户i(i=1, ..., N)是被其关注的用户的ID,是长度为4位的由数字和英文字母组成的字符串,各项间以空格分隔。
之后给出该用户点赞的信息:首先给出一个不超过10000的正整数M,随后M行,每行给出一个被其点赞的用户ID和对该用户的点赞次数(不超过1000),以空格分隔。注意:用户ID是一个用户的唯一身份标识。题目保证在关注列表中没有重复用户,在点赞信息中也没有重复用户。
Output
我们认为被该用户点赞次数大于其点赞平均数、且不在其关注列表上的人,很可能是其悄悄关注的人。根据这个假设,请你按用户ID字母序的升序输出可能是其悄悄关注的人,每行1个ID。如果其实并没有这样的人,则输出“Bing Mei You”。
思路:模拟,结构体排序。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int n, m, num;
std::string s[N], name;
struct node {
std::string name;
int cnt;
} e[N];
bool cmp(node a, node b) {
if(a.name < b.name) return true;
else return false;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n;
std::unordered_map<std::string, int> mp;
for(int i = 1; i <= n; i ++) {
std::cin >> s[i];
mp[s[i]] ++;
}
std::cin >> m;
int cnt = 0;
for(int i = 1; i <= m; i ++) {
std::cin >> name >> num;
e[i] = {name, num};
cnt += num;
}
double pre = cnt * 1.0 / m;
std::sort(e + 1, e + 1 + m, cmp);
int cc = 0;
for(int i = 1; i <= m; i ++) {
if(e[i].cnt > pre && !mp[e[i].name])
std::cout << e[i].name << '\n', cc ++;;
}
if(!cc)
std::cout << "Bing Mei You" << '\n';
return 0;
}L2-020 功夫传人
一门武功能否传承久远并被发扬光大,是要看缘分的。一般来说,师傅传授给徒弟的武功总要打个折扣,于是越往后传,弟子们的功夫就越弱…… 直到某一支的某一代突然出现一个天分特别高的弟子(或者是吃到了灵丹、挖到了特别的秘笈),会将功夫的威力一下子放大N倍 —— 我们称这种弟子为“得道者”。
这里我们来考察某一位祖师爷门下的徒子徒孙家谱:假设家谱中的每个人只有1位师傅(除了祖师爷没有师傅);每位师傅可以带很多徒弟;并且假设辈分严格有序,即祖师爷这门武功的每个第i代传人只能在第i-1代传人中拜1个师傅。我们假设已知祖师爷的功力值为Z,每向下传承一代,就会减弱r%,除非某一代弟子得道。现给出师门谱系关系,要求你算出所有得道者的功力总值。
Input
输入在第一行给出3个正整数,分别是:N(≤10^5)——整个师门的总人数(于是每个人从0到N−1编号,祖师爷的编号为0);Z——祖师爷的功力值(不一定是整数,但起码是正数);r ——每传一代功夫所打的折扣百分比值(不超过100的正数)。接下来有N行,第i行(i=0,⋯,N−1)描述编号为i的人所传的徒弟,格式为:
Ki ID[1] ID[2] ⋯ ID[Ki]
其中Ki是徒弟的个数,后面跟的是各位徒弟的编号,数字间以空格间隔。Ki为零表示这是一位得道者,这时后面跟的一个数字表示其武功被放大的倍数。
Output
在一行中输出所有得道者的功力总值,只保留其整数部分。题目保证输入和正确的输出都不超过10^10。
思路:模拟即可。注意祖师爷也可能是得道者!不然会悲惨-1。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
ll n, x, y, id;
double z, r, re[N];
ll mp[N];
std::vector<int> vec[N];
void DFS(int u) {
if(mp[u]) re[u] *= mp[u];
double c = re[u] * r;
for(auto v : vec[u]) {
re[v] = c;
DFS(v);
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n >> z >> r;
r = (100 - r) / 100;
for(int i = 0; i < n; i ++) {
std::cin >> x;
if(!x) {
std::cin >> y;
mp[i] = y;
}
for(int j = 1; j <= x; j ++) {
std::cin >> id;
vec[i].push_back(id);
}
}
re[0] = z;
DFS(0);
double ans = 0;
for(int i = 0; i < n; i ++) {
if(mp[i])
ans += re[i];
}
std::cout << (ll)ans << '\n';
return 0;
}