线性表详解

news2025/1/16 10:54:31

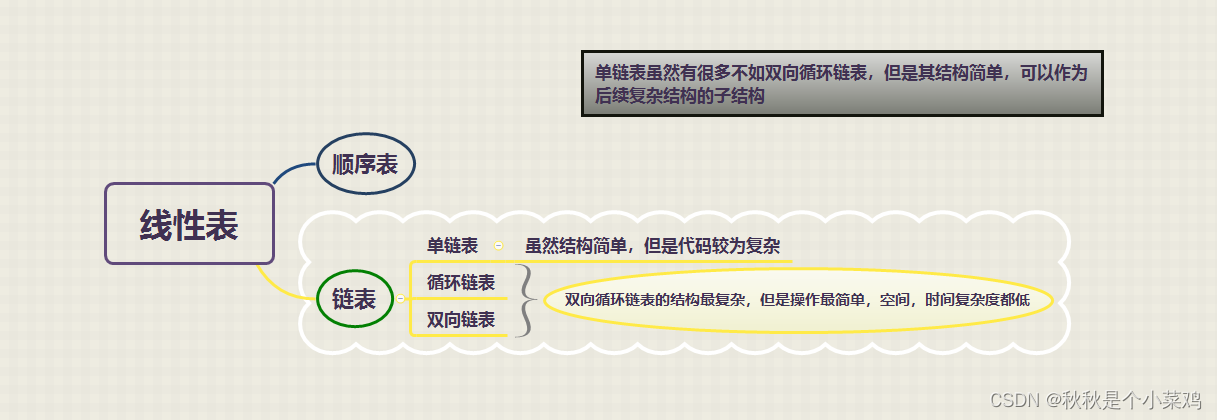
目录

1.线性表的定义和特点

2.案例

2.1一元多项式的计算

可以通过下面这个题目简单练习一下

2.2稀疏多项式的计算

2.3图书信息管理系统

3.线性表的类型定义

4.线性表的顺序表示和实现

4.1线性表的顺序储存表示

4.2顺序表中基本操作的实现

5.线性表的链式表现和实现

5.1单链表的定义和实现

5.2单链表的基本操作实现

5.3循环链表

5.4双向链表

6.顺序表和链表的比较

6.1空间性能

6.2时间性能

7.线性表的应用

7.1线性表的合并

7.2有序表的合并

8.小结

1.线性表的定义和特点

定义：由n（n≥0）个数据特性相同的元素构成的有限序列称为线性表。

线性表中的元素个数n定义为线性表的长度。n=0时为空链。

特点：

（1）存在唯一的一个被称为“第一个”的数据元素

（2）存在唯一的一个被称为“最后一个”的数据元素

（3）除第一个以外，结构中的每个数据元素均只有一个前驱；

（4）除最后一个以外，结构中的每个数据元素均只有一个后继；

2.案例

2.1一元多项式的计算

用两个线性表来储存系数，这样就转化为两个链表对应元素相操作的问题了

可以通过下面这个题目简单练习一下

剑指 Offer II 025. 链表中的两数相加 - 力扣（Leetcode）

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        //方法： 把所有数字压入栈中，再依次取出相加
        stack<int> s1, s2;
        while (l1) {
            //1.把l1中所有数字压入栈s1中
            s1.push(l1 -> val);
            l1 = l1 -> next;
        }
        while (l2) {
            //2.把把l2中所有数字压入栈s2中
            s2.push(l2 -> val);
            l2 = l2 -> next;
        }
        int carry = 0;

        ListNode* ans = nullptr;//用于储存最后返回的值
        
        while (!s1.empty() or !s2.empty() or carry != 0) {
            int a = s1.empty() ? 0 : s1.top();
            int b = s2.empty() ? 0 : s2.top();
            if (!s1.empty()) s1.pop();
            if (!s2.empty()) s2.pop();
            int cur = a + b + carry;
            carry = cur / 10;
            cur %= 10;
            auto curnode = new ListNode(cur);
            curnode -> next = ans;
            ans = curnode;
        }
        return ans;
    }
};

2.2稀疏多项式的计算

稀疏多项式的次幂跳度往往很大，这时如果再按照每个次幂来记录对应系数会有大量的0，比较浪费空间。这时我们采用（系数，指数）来记录多项式。

用一个长度为m且每个元素由两个数据线（系数项和指数项）的线性表。和多项式的计算其实差不多，不过原来简单多项式的线性表元素是单个数，稀疏多项式用的是（m，n）这样的数对。

具体的代码在后面介绍（c++中有个很好的结构叫做（pair）键值对，在树的对应章节会介绍）

2.3图书信息管理系统

出版社有一些图书数据保存在一个文本文件 book . txt 中，为简单起见，在此假设每种图书只包括三部分信息： ISBN （书号）、书名和价格，文件中的部分数据如图2.1所示。现要求实现一个图书信息管理系统，包括以下6个具体功能。
(1）查找：根据指定的 ISBN 或书名查找相应图书的有关信息，并返回该图书在表中的位置序号。(2）插人：插入一种新的图书信息。
(3）删除：删除一种图书信息。
(4）修改：根据指定的 ISBN ，修改该图书的价格。
(5）排序：将图书按照价格由低到高进行排序。
(6）计数：统计图书表中的图书数量。
要实现上述功能，与以上案例中的多项式一样，我们首先根据图书表的特点将其抽象成一个线性表，每本图书作为线性表中一个元素，然后可以采用适当的存储结构来表示该线性表，在此基础上设计完成有关的功能算法。具体采取哪种存储结构，可以根据两种不同存储结构的优缺点，视实际情况而定。

具体代码实现会在后面单独的一篇博文给出

3.线性表的类型定义

说明：

（1）出翔数据类型进士一个模型的定义，不涉及模型的具体实现（不是某种语言的代码实现），下面描述的所涉及参数不考虑具体数据类型；

（2）下面抽象数据类型中给出的操作只是基本的操作。

ADT List{
数据对象：D={ai|ai∈ElemSet,i=1,2,...n,n≥0}
数据操作关系：R={<ai-1,ai>,ai∈D,i=2,...,n}
基本操作；
InitList(&L)
操作结果：构造一个空的线性表L（初始化）
DestoryList(&L)
初始条件：线性表L已经存在
操作结果：销毁线性表L
ClearList(&L)
初始条件：线性表L已经存在
操作结果：将线性表L重置为空表
ListEmpty(L)
初始条件：线性表L已经存在
操作结果：若线性表L为空表，返回true，若不是，返回false
ListLength(L)
初始条件：线性表L已经存在
操作结果：返回线性表L中数据元素个数
GetElem(L,i,&e)
初始条件：线性表L已经存在,且1≤i≤ListLength(L)
操作结果：用e返回L中第i个数据元素的值
LocateElem(L,e)
初始条件：线性表L已经存在
操作结果：用e返回L中第1个和e相同的元素在L中的位置。若这样的值不存在，则返回值为空值
ProirElem(L,cur_e,&pre_e)
初始条件：线性表L已经存在
操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_e返回其前驱，否则操作失败，pre_e无定义
NextElem(L,cur_e,&next_e)
初始条件：线性表L已经存在
操作结果：若cur_e是L的数据元素，且不是最后一个，则用next_e返回其前驱，否则操作失败，next_e无定义
ListInsert(&L,i,e)
初始条件：线性表L已经存在且1≤i≤ListLength(L)
操作结果：在L中的第i个位置之前按插入新的元素e，L的长度+1.
ListDelete(&L,i)
初始条件：线性表L已经存在且非空，且1≤i≤ListLength(L)
操作结果：删除L中的第i个位置的元素，L的长度-1.
TraverseList(L)
初始条件：线性表L已经存在
操作结果：对线性表L进行遍历，在遍历过程中对L的每个元素访问一次。

4.线性表的顺序表示和实现

4.1线性表的顺序储存表示

定义：用一组地址连续的存储单元一次存储线性表的数据元素，这种表示方法也称作顺序储存结构或顺序映像。通常，称这种存储结构的线性表为顺序表

特点：逻辑上相邻的元素，物理位置上也相邻。

在c语言中可以用动态分配的一维数组来表示线性表，描述如下

#define N 200
typedef int SLDataType;
struct SeqList
{
    SLDataType *elem;  //存储空间的基地址
	int length;        //当前长度
}SqList;               //顺序表的结构类型为SqList

4.2顺序表中基本操作的实现

//顺序表中基本操作的实现
//初始化
bool InitList(SeqList& L)
{
	L.elem = new SLDataType[N];
	if (!L.elem) exit(-1);
	L.length = 0;
	return true;
}
//取值
bool GetElem(SeqList L, int i, SLDataType& e) {
	if (i<1 || i>L.length) return false;

	e = L.elem[i - 1];
	return true;
}
//查找
int LocateElem(SeqList L,SLDataType e)
{
	for (int i = 0;i < L.length;i++)
	{
		if (L.elem[i] == e) 
			return i + 1;
	}
	return 0;
}
//插入
bool ListInsert(SeqList& L, int i, SLDataType e)
{
	if ((i < 1) || (i > L.length + 1))return false;
	if (L.length == N) return false;
	
	for (int j = L.length - 1;j >= i - 1;j++)
	{
		L.elem[j + 1] = L.elem[j];
		L.elem[i - 1] = e;
		L.length++;

		return true;
	}
}

//删除
bool ListDelete(SeqList& L, int i)
{
	if ((i < 1) || (i > L.length)) return false;
	for (int j = i;j <= L.length - 1;j++)
	{
		L.elem[j - 1] = L.elem[j];
		L.length--;
	}
	return true;
}

5.线性表的链式表现和实现

静态顺序表存在一个问题：N太小，可能不够用，N太大，可能浪费空间，所以很多时候链式线性表更为常用。

5.1单链表的定义和实现

特点：用一组任意的春初单元存储线性表的数据元素

定义：

//1.定义
typedef int SLDataType;

typedef struct LNode {
	SLDataType data;	/*数据域*/
	struct LNode* next; /*指针域*/
}LNode,*LinkList;

5.2单链表的基本操作实现

//2.初始化
bool InitList(LinkList& L)
{
	L = new LNode;
	L->next = NULL;
	return true;
}

//3.取值
bool GetElem(LinkList L,int i, SLDataType& e)
{
	LNode *p = L->next;
	int j = 1;
	while (p && j < i)
	{
		p = p->next;
		j++;
	}
	if (!p || j > i) 
		return false;

	e = p->data;
	return true;
}

//4.查找
LNode* LocateElem(LinkList L, SLDataType e)
{
	LNode* p = L->next;
	while (p && p->data != e)
	{
		p = p->next;
	}
	return p;
}


//5.插入
bool ListInsert(LinkList L,int i,SLDataType e)
{
	LNode* p = L;int j = 0;
	while (p && (j < i - 1))
	{
		p = p->next;
		j++;
	}
	if (!p || j > i - 1)
		return false;

	LNode* s = new LNode;
	s->data = e;
	s->next = p->next;
	p->next = s;

	return true;
}

//6.删除
bool ListDelete(LinkList& L, int i)
{
	LNode* p = L;
	int j = 0;

	while ((p->next) && j < i - 1)
	{
		p = p->next;j++;
	}
	if (!p || j > i - 1)
		return false;
}


//前插法创建单链表
void CreateList_H(LinkList& L, int n)
{
	L = new LNode;
	L->next = NULL;
	
	for (int i = 0;i < n;i++)
	{
		LNode* p  = new LNode;
		cin >> p->data;
		p->next = L->next;
		
		L->next = p;

	}
}

//后插法创建新链表
void CreateList_R(LinkList& L, int n)
{
	LNode* L = new LNode;
	LinkList r = L;
	for (int i = 0;i < n;++i)
	{
		LNode *p = new LNode;
		cin >> p->data;

		p->next = NULL;r->next = p;
		r = p;
	}
}

5.3循环链表

特点：表中最后一个节点的指针域指向头结点

操作与单链表基本类似。

区别：遍历链表的判别条件不同，为 p!=NULL或者p->next!=NULL;

5.4双向链表

✍双向链表几乎和单向列表一样。唯一的不同是每一个节点都要两个指针。与单向列表相同的是他的继承点都指向下一个节点（如果存在）。但是每个节点有一个额外的指针指向前面的一个节点（如果存在）。

使用这个额外的指针能够让我们从链表的末尾开始向前迭代，但是这样会使用两倍的内存。但是他的好处是我们会很容易的搜索，插入或者 删除比较靠后的节点，其时间复杂度是O（1）。如果用单向列表做那么时间复杂度为O（n）。

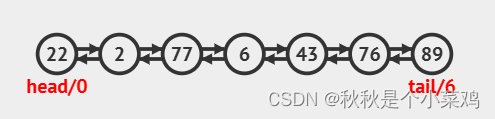
 不带头结点的单链表是链表的最简单的一种结构，最复杂的一种结构是带有头结点的双向循环链表。

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int LTDataType;
typedef struct ListNode
{
	struct ListNode* next;		//指向直接前驱
	struct ListNode* prev;		//指向直接后继
	LTDataType data;			//数据域
}LTNode;


LTNode* BuyListNode(LTDataType x)
{
	LTNode* node = (LTNode*)malloc(sizeof(LTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	node->data = x;
	node->next = NULL;
	node->prev = NULL;
	return node;
}

//void ListInit(LTNode** pphead)
//{
//	*pphead = BuyListNode(-1);
//	(*pphead)->next = *pphead;
//	(*pphead)->prev = *pphead;
//}

LTNode* ListInit()
{
	LTNode* phead = BuyListNode(-1);
	phead->next = phead;
	phead->prev = phead;

	return phead;
}

void ListPrint(LTNode* phead)
{
	assert(phead);

	LTNode* cur = phead->next;
	while (cur != phead)
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

void ListPushBack(LTNode* phead, LTDataType x)
{
	assert(phead);

	/*LTNode* newnode = BuyListNode(x);
	LTNode* tail = phead->prev;
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;*/

	ListInsert(phead, x);

}

void ListPushFront(LTNode* phead, LTDataType x)
{
	assert(phead);

	//LTNode* newnode = BuyListNode(x);
	//LTNode* next = phead->next;

	 phead newnode next
	//phead->next = newnode;
	//newnode->prev = phead;
	//newnode->next = next;
	//next->prev = newnode;

	ListInsert(phead->next, x);
}

//void ListPushFront(LTNode* phead, LTDataType x)
//{
//	assert(phead);
//
//	LTNode* newnode = BuyListNode(x);
//
//	phead->next->prev = newnode;
//	newnode->next = phead->next;
//
//	phead->next = newnode;
//	newnode->prev = phead;
//}

void ListPopBack(LTNode* phead)
{
	assert(phead);

	assert(phead->next != phead);
	//assert(!ListEmpty(phead));

	/*LTNode* tail = phead->prev;
	LTNode* tailPrev = tail->prev;

	free(tail);

	tailPrev->next = phead;
	phead->prev = tailPrev;*/

	ListErase(phead->prev);
}

void ListPopFront(LTNode* phead)
{
	assert(phead);
	assert(phead->next != phead);

	ListErase(phead->next);
}

bool ListEmpty(LTNode* phead)
{
	assert(phead);

	return phead->next == phead;
}

// 在pos位置之前插入x
void ListInsert(LTNode* pos, LTDataType x)
{
	assert(pos);
	LTNode* prev = pos->prev;
	LTNode* newnode = BuyListNode(x);

	// prve newnode pos
	prev->next = newnode;
	newnode->prev = prev;
	newnode->next = pos;
	pos->prev = newnode;
}

//  删除pos位置的节点
void ListErase(LTNode* pos)
{
	assert(pos);
	LTNode* prev = pos->prev;
	LTNode* next = pos->next;

	prev->next = next;
	next->prev = prev;
	free(pos);
}

6.顺序表和链表的比较

6.1空间性能

（1）储存空间的比较

顺序表的存储空间必须预先分配，元素个数扩充受到一定限制，易造成存储空间的浪费或者空间一处现象。链表则不需要预先分配空间，对空间的利用更充分。

（2）存储密度的大小

存储密度=数据元素本身所占存储量/节点结构占用的存储量。如果不考虑

6.2时间性能

（1）存取性能的比较

顺序表---O(1)         链表---O(n)

（2）删除和插入

顺序表---O(n)     链表---O(1) 

7.线性表的应用

7.1线性表的合并

可以参考这个题目的练习

1669. 合并两个链表 - 力扣（Leetcode）

class Solution {
public:
    ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {
        ListNode* preA = list1;
        for (int i = 0; i < a - 1; i++) {
            preA = preA->next;
        }
        ListNode* preB = preA;
        for (int i = 0; i < b - a + 2; i++) {
            preB = preB->next;
        }
        preA->next = list2;
        while (list2->next != nullptr) {
            list2 = list2->next;
        }
        list2->next = preB;
        return list1;
    }
};



 

7.2有序表的合并

21. 合并两个有序链表 - 力扣（Leetcode）

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (l1 == NULL) {
            return l2;
        }
        if (l2 == NULL) {
            return l1;
        }
        if (l1->val <= l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        }
        l2->next = mergeTwoLists(l1, l2->next);
        return l2;
    }
};

8.小结

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/435539.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

vba：inputbox

vba：inputbox

inputbox函数与方法 1.区别一&#xff1a;外观区别 InputBox 函数 在一对话框来中显示提示&#xff0c;等待用户输入正文或按下按钮&#xff0c;并返回包含文本框内容的 String。 Application.InputBox 方法 显示一个接收用户输入的对话框。返回此对话框中输入的信息。 -----…
阅读更多...
分享一个国内使用的ChatGPT的方法

分享一个国内使用的ChatGPT的方法

介绍 ChatGPT ChatGPT是一种基于自然语言处理技术的对话生成模型。它是由OpenAI公司开发的一种语言模型&#xff0c;可以在大规模语料库上进行无监督学习&#xff0c;并生成高质量的自然语言文本。ChatGPT可以用于多种应用场景&#xff0c;例如智能客服、语音助手、聊天机器人…
阅读更多...
JAVA学习笔记（注解）

JAVA学习笔记（注解）

1. JDK预定义注解 (1) Deprecated&#xff08;表示标记对象已过时&#xff09; (2) SuppressWarnings("all") &#xff08;忽略标记对象的警告&#xff09; 2. 元注解&#xff08;用于描述注解的注解&#xff09; Target 描述注解所生效的位置 Retention 描述注…
阅读更多...
SpringBooot

SpringBooot

目录 一、简介 1、使用原因 2、JavaConfig &#xff08;1&#xff09;Configuration注解 &#xff08;2&#xff09;Bean注解 &#xff08;3&#xff09;ImportResource注解 &#xff08;4&#xff09;PropertyResource注解 &#xff08;5&#xff09;案例 3、简介 4…
阅读更多...
Faster-RCNN代码解读8：代码调试与总结

Faster-RCNN代码解读8：代码调试与总结

Faster-RCNN代码解读8&#xff1a;代码调试与总结 前言 ​ 因为最近打算尝试一下Faster-RCNN的复现&#xff0c;不要多想&#xff0c;我还没有厉害到可以一个人复现所有代码。所以&#xff0c;是参考别人的代码&#xff0c;进行自己的解读。 ​ 代码来自于B站的UP主&#xff0…
阅读更多...
网络协议-前端重点——DNS和CDN

网络协议-前端重点——DNS和CDN

目录 DNS的基础知识 统一资源定位符&#xff08;URL&#xff09;&#xff08;网址&#xff09; DNS&#xff08;Dimain Name System&#xff09;(域名系统) DNS Query过程 DNS记录 A记录 AAAA记录 CNAME记录&#xff08;Canonical Name Record&#xff09; MX记录&#…
阅读更多...
Blender3.5 视图切换

Blender3.5 视图切换

目录 1. 数字小键盘切换视图1.1 正交顶视图1.2 正交前视图1.3 正交右视图1.4 透视图1.5 四格视图 2. 鼠标点击切换视图2.1 点击视图&#xff0c;根据需求选择对应视图2.2 点导航栏的坐标轴切换 3. 启用字母区数字键3.1 编辑——偏好设置——输入——勾选“模拟数字键” 1. 数字…
阅读更多...
Linux驱动——高级I/O操作（四）

Linux驱动——高级I/O操作（四）

目录 几种I/O模型总结 异步通知 几种I/O模型总结 阻塞 IO:在资源不可用时&#xff0c;进程阻塞&#xff0c;阻塞发生在驱动中&#xff0c;资源可用后进程被唤醒,在阻塞期间不占用CPU&#xff0c;是最常用的一种方式。 非阻塞 I/O: 调用立即返回&#xff0c;即便是在资…
阅读更多...
《Unity Shader 入门精要》第10章 高级纹理

《Unity Shader 入门精要》第10章 高级纹理

第10章 高级纹理 10.1 立方体纹理 在图形学中&#xff0c;立方体纹理 &#xff08;Cubemap&#xff09; 是环境映射 &#xff08;Environment Mapping&#xff09; 的一种实现方法。 和之前见到的纹理不同&#xff0c;立方体纹理一共包含了6张图像&#xff0c;这些图像对应了…
阅读更多...
typescript的keyof的用法

typescript的keyof的用法

第一种&#xff1a;与接口一起用&#xff0c;返回联合类型 interface Person {name: string;age: number;location: string;}type K1keyof Person; // "name" | "age" | "gender" let a:K1name 第二种&#xff1a;与typeof一起用&#xff0c;可…
阅读更多...
天梯赛练习（L2-013 ~ L2-020）

天梯赛练习（L2-013 ~ L2-020）

L2-013 红色警报 战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序&#xff0c;当失去一个城市导致国家被分裂为多个无法连通的区域时&#xff0c;就发出红色警报。注意&#xff1a;若该国本来就不完全连通&#xff0c;是分裂的k个区域&#xff0c;而失去一…
阅读更多...
【springcloud开发教程】负载均衡——Ribbon

【springcloud开发教程】负载均衡——Ribbon

Ribbon是什么&#xff1f; Spring Cloud Ribbon 是基于Netflix Ribbon 实现的一套客户端负载均衡的工具。简单的说&#xff0c;Ribbon 是 Netflix 发布的开源项目&#xff0c;主要功能是提供客户端的软件负载均衡算法&#xff0c;将 Netflix 的中间层服务连接在一起。Ribbon 的…
阅读更多...
CentOS7安装docker以及docker-compose

CentOS7安装docker以及docker-compose

前言 系统版本&#xff1a;CentOS7.9 docker版本&#xff1a;当前最新版本是23.0.3 docker compose版本&#xff1a;v2.17.2 参考官网文档&#xff1a;跳转链接 安装docker 删除原有的docker&#xff08;如果有的话&#xff09; sudo yum remove docker \docker-client …
阅读更多...
CSAPPLab1-DataLab

CSAPPLab1-DataLab

1、bitXor 异或&#xff1a;不是同时为0和不是同时为1的情况进行按位与 /** bitXor - x^y using only ~ and &* Example: bitXor(4, 5) 1* Legal ops: ~ &* Max ops: 14* Rating: 1*/int bitXor(int x, int y) {return ~(~x & ~y) & ~(x & y); } …
阅读更多...
可鉴别加密工作模式-同时保护数据机密性和完整性（OCB、CCM、KeyWrap、EAX和GCM）第一部分

可鉴别加密工作模式-同时保护数据机密性和完整性（OCB、CCM、KeyWrap、EAX和GCM）第一部分

当算法用于同时保护数据的机密性和完整性时&#xff0c;应选取合适的可鉴别加密工作模式&#xff0c;例如OCB、CCM、KeyWrap、EAX和GCM等工作模式。以下总结来自GBT36624-2018国标文本。 在可鉴别加密工作模式之前&#xff0c;先来说说分组密码的工作模式可参考GBT17964-2021版…
阅读更多...
反欺诈（羊毛盾）API 实现用户行为分析的思路分析

反欺诈（羊毛盾）API 实现用户行为分析的思路分析

简介 反欺诈&#xff08;羊毛盾&#xff09;API 是一种用于识别和防范各种欺诈行为的技术解决方案。它可集成到各种应用程序和平台中&#xff0c;通过手机号码、手机IP进行异常检测&#xff0c;达到防范恶意注册、虚假评论、虚假交易等欺诈行为的目的。 本文主要介绍反欺诈&a…
阅读更多...
1677_MIT 6.828 xv6中增加CPU alarm

1677_MIT 6.828 xv6中增加CPU alarm

全部学习汇总&#xff1a; GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 前面把课程要求做了一个简单的翻译&#xff0c;从课程的要求说明中其实已经能够得到很多的提示。这个alarm的功能&#xff0c;其实有点类似回调函数的概念&#xf…
阅读更多...
基于springboot+mysql+jsp实现校园新闻发布系统

基于springboot+mysql+jsp实现校园新闻发布系统

基于springbootmysqljsp实现校园新闻发布系统 一、系统介绍1、系统主要功能&#xff1a;2.涉及技术框架&#xff1a;3.本项目所用环境&#xff1a; 二、功能展示三、其它系统四、获取源码 一、系统介绍 1、系统主要功能&#xff1a; 普通用户&#xff1a;浏览主页面&#xff…
阅读更多...
【音视频处理】直播工作原理，直播CDN、推流拉流、流媒体服务究竟是什么

【音视频处理】直播工作原理，直播CDN、推流拉流、流媒体服务究竟是什么

大家好&#xff0c;欢迎来到停止重构的频道。 本期我们讨论直播技术。 我们将会介绍&#xff0c;直播工作原理&#xff0c;流媒体服务的作用&#xff0c;推流/拉流、直播CDN等等。 这里需要特别说明的是&#xff0c;直播指的是&#xff1a;1对多的直播&#xff0c;平常直播平…
阅读更多...
基于copula的风光联合场景生成与缩减

基于copula的风光联合场景生成与缩减

目录 1 主要内容 风光出力场景生成方法 2 部分程序 3 程序结果 4 程序链接 点击直达&#xff01; 1 主要内容 该程序方法复现《融合风光出力场景生成的多能互补微网系统优化配置》风光出力场景生成部分&#xff0c;目前大多数研究的是不计风光出力之间的相关性影响&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023