目录
一、前言
二、二维绘图
1、曲线图、散点图plot
2、隐函数、显函数与参数方程的绘图
①ezplot
②fplot
三、三维绘图
1、单曲线plot3
2、多曲线plot3
3、曲面
①实曲面surf
②网格曲面mesh
四、特殊的二维、三维图
1、极坐标图polar
2、平面散点图scatter
3、平面等值线图contour
4、空间等值线图contour3
5、三维散点图scatter3
五、处理图形
一、前言
绘图可以说是MATLAB的精髓了。想当初小编在做高数题想不出来的时候,还用过MATLAB画过几次图,偷偷把答案算出来,可以说是加满了狠活儿与科技。当然了如果有小伙伴们对Python作图感兴趣,可以看看小编写的另外两篇博客:
python数据可视化之matplotlib实践 基础篇(1)_下载matplotlib库_计算机鬼才~的博客-CSDN博客
python数据可视化之matplotlib实践 基础篇(2)_matplotlib hatch_计算机鬼才~的博客-CSDN博客
本篇博客我们将从二维图像、三维图像两个方面来讲如何使用MATLAB绘图。
二、二维绘图
1、曲线图、散点图plot
MATLAB作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给MATLAB函数画图。
调用方法:plot(X,Y,S)
参数说明:X,Y是向量,分别表示点集的横坐标和纵坐标,S代表线的类型,具体如下
| 符号 | 线型 | 符号 | 线型 |
| y | 黄色 | c | 蓝绿色 |
| b | 蓝色 | g | 绿色 |
| m | 粉红 | r | 红色 |
| . | 点 | o | 圈 |
| + | +号 | x | x |
| -- | 长虚线 | : | 短虚线 |
分段函数图:plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn)
我们来画一个三角函数与反三角函数:
x=linspace(-pi,pi,30);
y=asin(x);
z=cos(x);
plot(x,y,'x',x,z,'g')

2、隐函数、显函数与参数方程的绘图
①ezplot
| 函数 | 作用说明 |
| ezplot(‘f(x)’,[a,b]) | 表示在a<x<b绘制显函数f=f(x)的函数图. |
| ezplot(‘f(x,y)’,[xmin,xmax,ymin,ymax]) | 表示在区间xmin<x<xmax和 ymin<y<ymax绘制隐函数f(x,y)=0的函数图. |
| ezplot(‘x(t)’,’y(t)’,[tmin,tmax]) | 表示在区间tmin<t<tmax绘制参数方程x=x(t),y=y(t)的函数图 |
绘画:
A.函数在[0,3]的图像
ezplot('x^3-4 ', [0,3]) 
B.隐函数在x
[0,5],y
[-4,0]的图像
ezplot('exp(x)+y^3',[0,5,-4,0]) 
C.参数函数在参数范围为[0,
]的图像
ezplot('cos(t)^3','sin(t)^3', [0,2*pi])
②fplot
函数:fplot(‘fun’,lims)
作用说明:表示绘制字符串fun指定的函数在lims=[xmin,xmax]的图形.
额外说明:[1] fun必须是M文件的函数名或是独立变量为x的字符串
[2] fplot函数不能画参数方程和隐函数图形,但在一个图上可以画多个图形
三、三维绘图
1、单曲线plot3
函数:plot3(x,y,z,s)
作用说明:x,y,z分别表示曲线上点集的横坐标、纵坐标、函数值,S代表曲线颜色
例如:在区间[0,10π]画出参数曲线 x=sint,y=cost, z=t。
t=0:pi/100:10*pi;
plot3(sin(t),cos(t),t)
rotate3d
2、多曲线plot3
函数:plot3(x,y,z)
作用说明:其中x,y,z是都是m×n矩阵,其对应的每一列表示一条曲线
例如:画多条曲线观察函数
x=-3:0.1:3;y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
plot3(X,Y,Z)
3、曲面
①实曲面surf
函数:surf(x,y,z)
作用说明:画出数据点(x,y,z)表示的曲面
例如:画函数的图形
x=-3:0.1:3;
y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
surf(X,Y,Z)
shading flat
rotate3d

②网格曲面mesh
函数:mesh(x,y,z)
作用说明:画出数据点(x,y,z)表示的网格曲面
例如:画出曲面在不同视角的网格图
x=-3:0.1:3;
y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
mesh(X,Y,Z) 
四、特殊的二维、三维图
1、极坐标图polar
函数:polar (theta,rho,s)
作用说明:用角度theta即(弧度表示)和极半径rho即
作极坐标图,用s指定线型
例如:绘画极坐标曲线
theta=linspace(0,2*pi),
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho,'g')
title('Polar plot of sin(2*theta).*cos(2*theta)');
2、平面散点图scatter
函数:scatter(X,Y,S,C)
作用说明:在向量X和Y的指定位置显示彩色圈.X和Y必须大小相同
3、平面等值线图contour
函数:contour(x,y,z,n)
作用说明:绘制n个等值线的二维等值线图
[X,Y]=meshgrid(-2:.2:2,-2:.2:3);
Z=X.*exp(-X.^2-Y.^2);
[C,h]=contour(X,Y,Z);
clabel(C,h)
colormap cool
4、空间等值线图contour3
函数:contour 3(x,y,z,n)
作用说明:其中n表示等值线数
[x,y,z]=peaks;
subplot(1,2,1)
contour3(x,y,z,16,'s')
grid, xlabel('x-axis'),ylabel('y-axis')
zlabel('z-axis')
title('contour3 of peaks');
subplot(1,2,2)
contour(x,y,z,16,'s')
grid, xlabel('x-axis'), ylabel('y-axis')
title('contour of peaks');

5、三维散点图scatter3
函数:scatter3(X,Y,Z,S,C)
作用说明:在向量X,Y和Z指定的位置上显示彩色圆圈,且向量X,Y和Z的大小必须相同
[x,y,z]=sphere(16);
X=[x(:)*.5 x(:)*.75 x(:)];
Y=[y(:)*.5 y(:)*.75 y(:)];
Z=[z(:)*.5 z(:)*.75 z(:)];
S=repmat([1 .75 .5]*10,prod(size(x)),1);
C=repmat([1 2 3],prod(size(x)),1);
scatter3(X(:),Y(:),Z(:),S(:),C(:),'filled'),view(-60,60)

五、处理图形
| 函数方法 | 作用 |
| GRID ON | 加格栅在当前图上 |
| GRID OFF | 删除格栅 |
| hh = xlabel(string) | 在当前图形的x轴上加图例string |
| hh = ylabel(string) | 在当前图形的y轴上加图例string |
| hh = zlabel(string) | 在当前图形的z轴上加图例string |
| hh = title(string) | 在当前图形的顶端上加图例string |
| hold on | 保持当前图形, 以便继续画图到当前图上 |
| hold of | 释放当前图形窗口 |
例如:在区间[0,10π]画出参数曲线 x=sint,y=cost, z=t,并加入相关的文字。
t=0:pi/100:10*pi;
plot3(sin(t),cos(t),t)
xlabel('自变量X')
ylabel('自变量Y')
zlabel('函数Z')
title('示意图')
grid on
rotate3d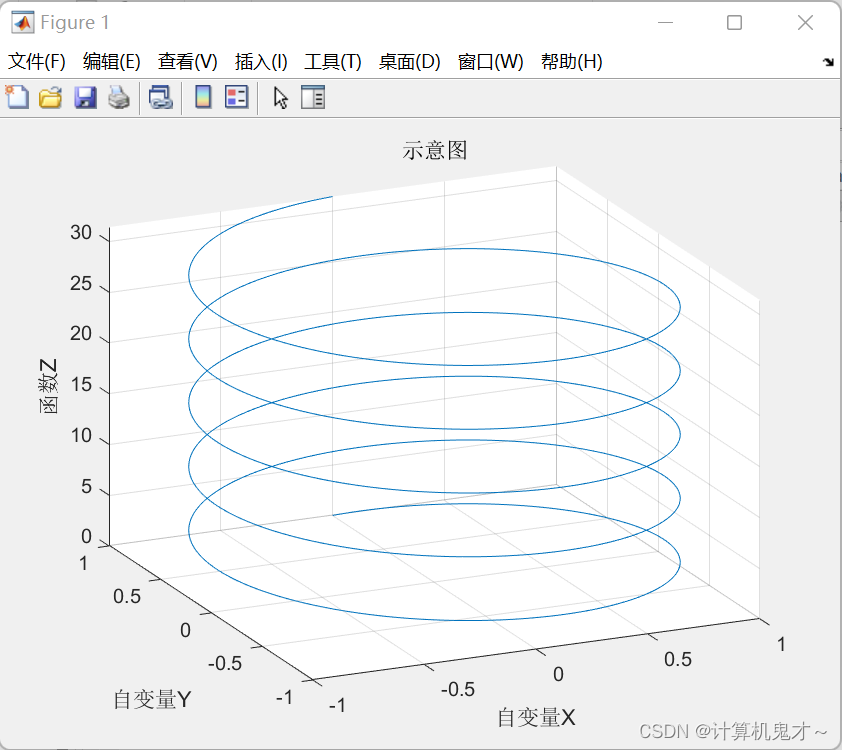
好的,数学建模学习的第二天,不知道大家学会了多少呢?如果对大家有所帮助,麻烦大家给我一个免费的小心心吧!