学习目标：

要学习向量与矩阵的范数，我会采取以下几个步骤：

1. 了解基本概念：首先，我会了解向量和矩阵的范数的基本概念和定义，以及它们的性质和特点，这是理解和掌握范数的基础。

2. 学习具体算法：其次，我会学习具体的算法和计算方法，如计算向量的L1、L2、无穷范数，计算矩阵的1范数、2范数、无穷范数等等。我会在学习过程中多做一些例题，理解范数的计算方法和应用场景。

3. 掌握范数的应用：在学习范数的过程中，我会关注范数在实际问题中的应用，如在机器学习、信号处理、图像处理等领域中的应用，通过实际问题的分析和解决，加深对范数的理解和应用能力。

4. 建立数学模型：在学习范数的应用中，我会注意建立数学模型，把实际问题抽象成数学模型，并应用范数的概念和算法进行求解，这可以帮助我更好地理解和掌握范数的应用。

5. 不断练习和总结：最后，我会进行练习和总结，通过多做练习题、实际问题分析和总结经验，不断提高自己的范数应用能力和解决问题的能力。同时，我会保持学习的热情和耐心，不断探索和挑战更深层次的数学知识和应用。

---

 3.3.1 向量的范数：

向量的范数是一种衡量向量大小的方法。它可以被定义为一个非负实数，表示为 ||x||，其中 x 是一个 n 维向量。向量的范数可以被定义为以下三种类型之一：

1. L1 范数：也称为曼哈顿范数，它是向量元素绝对值之和，表示为 ||x||1。它衡量的是向量中各个元素的绝对大小之和。

2. L2 范数：也称为欧几里得范数，它是向量元素的平方和的平方根，表示为 ||x||2。它衡量的是向量的长度或模，即该向量到原点的欧几里得距离。

3. 无穷范数：也称为切比雪夫范数，它是向量元素绝对值的最大值，表示为 ||x||∞。它衡量的是向量中最大元素的绝对值。

这些范数之间有着不同的性质和应用场景。L1 范数适用于希望强制稀疏性或鼓励特征选择的问题。L2 范数适用于希望强制平滑或鼓励权重衰减的问题。而无穷范数适用于希望强制元素间最大差距或最大误差的问题。

 3.3.2 矩阵的范数

矩阵的范数（Matrix norm）是矩阵理论中的一个重要概念，它衡量了矩阵的大小或者变换的幅度，类似于向量的范数。

矩阵的范数定义为一个函数，把一个矩阵映射到实数，具体来说，矩阵的范数 $| \cdot |$ 满足以下条件：

1. 非负性：对于任意矩阵 A，有 |A| \geq 0。

2. 齐次性：对于任意矩阵 A 和任意实数 alpha，有 \alpha | = |\alpha| |A|。

3. 三角不等式：对于任意矩阵 A和 B，有 |A+B| \leq |A|+|B|。

通常情况下，矩阵的范数可以有多种定义方式，常用的包括：

1. L^p 范数：p 阶范数定义为 |A|p = (\sum{i,j}|a_{i,j}|^p)^{1/p}，其中 a_{i,j} 是矩阵 A 的元素。

2. 2-范数（或者谱范数）：矩阵的 2-范数定义为 |A|2 = \sqrt{\lambda{\max}(A^TA)}，其中 \lambda_{\max}(A^TA)是矩阵 A^TA的最大特征值。

3. Frobenius 范数：Frobenius 范数定义为 |A|F = \sqrt{\sum{i,j}|a_{i,j}|^2}，其中 a_{i,j}是矩阵 A的元素。

不同的范数适用于不同的情况和问题，选择合适的范数可以帮助我们更好地理解矩阵的性质和特点，也有利于在矩阵计算中做出更好的决策和优化。

 3.3.2 算子范数

矩阵的算子范数（Operator norm），也称为矩阵的最大列模数（Maximum column norm），是矩阵范数的一种常见形式，它对矩阵的列向量的伸缩性进行度量。对于一个 m \times n的矩阵 A，其算子范数定义为：

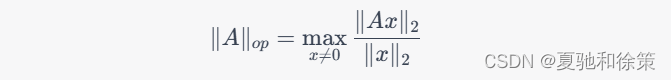
其中，|x|_2 表示 x 的 L^2范数，即 |x|2 = \sqrt{\sum{i=1}^n x_i^2}。算子范数可以理解为矩阵对于向量的最大缩放比例，即它衡量了矩阵对于输入向量的最大放大效应。

算子范数有多种计算方式，常用的包括以下几种：

1. 1-范数：算子范数可以定义为矩阵列向量的 $L^1$ 范数的最大值，即 |A|{op} = \max{j=1,\ldots,n}\sum_{i=1}^m |a_{ij}|。

2. $\infty$-范数：算子范数也可以定义为矩阵行向量的 L^{\infty}范数的最大值，即 |A|{op} = \max{i=1,\ldots,m}\sum_{j=1}^n |a_{ij}|。

3. 2-范数：算子范数可以表示为矩阵的最大奇异值，即 |A|{op} = \sigma{\max}(A)，其中 \sigma_{\max}(A) 是矩阵 A 的最大奇异值。

算子范数的选择取决于所涉及的问题和应用场景，不同的范数可能有不同的计算复杂度和准确性，因此需要根据具体情况选择最合适的算子范数。

 总结：

向量和矩阵的范数是线性代数中的重要概念，其应用广泛，涉及到很多领域，如数值计算、信号处理、统计学等等。以下是向量和矩阵范数的重点和难点，以及容易出错的地方：

1. 定义和性质：向量和矩阵范数的定义和性质是理解和计算范数的关键，要熟练掌握每种范数的定义和常用性质，如正定性、三角不等式等等。

2. 计算方法：向量和矩阵范数的计算方法不同，需要根据不同的范数选择合适的计算方法，如 L^p范数可以使用幂函数计算，算子范数需要计算矩阵的最大奇异值等等。

3. 应用场景：不同的向量和矩阵范数适用于不同的问题和应用场景，需要根据具体情况选择最合适的范数，如欧几里得范数适用于距离计算，而 L^1 范数适用于稀疏表示等等。

4. 精度和稳定性：范数计算的精度和稳定性是另一个需要注意的问题，由于计算过程中可能涉及到浮点数舍入误差和数值不稳定性等问题，因此需要注意计算过程中的精度和稳定性。

5. 矩阵的特征值和奇异值：矩阵范数通常涉及到矩阵的特征值和奇异值，需要对矩阵的特征值和奇异值有一定的了解，特别是对于算子范数和谱范数等需要计算矩阵的特征值和奇异值的范数。

6. 矩阵的维度和尺寸：在计算矩阵范数时需要注意矩阵的维度和尺寸，不同的范数对于矩阵的维度和尺寸有不同的要求，需要注意选择合适的范数和矩阵大小。