Author: Tianjiao Ding, Shengbang Tong, Kwan Ho Ryan Chan, Xili Dai, Yi Ma, Benjamin D. Haeffele
Abstract
在本文中,我们建议同时执行聚类并通过最大编码率降低来学习子空间联合表示。 对合成和现实数据集的实验表明,所提出的方法实现了与最先进的替代方法相当的聚类精度,同时更具可扩展性和学习几何意义的表示。
1. Introduction
- 我们建议同时对数据进行聚类并通过MCR 2 ^2 2 学习正交子空间并集表示,此时假定数据位于流形并集。 这是通过公式 (4) 实现的,该公式优化了表示和受最先进的子空间聚类结果启发的双随机成员公式。
- 我们给出了membership的参数化(图 2)。 此外,由于问题 (4) 是高度非凸的,我们给出了一个关于如何初始化变量和优化它的元算法(算法 1)。
- 我们在仿真和 CIFAR10 上进行实验,以证明所提出方法的一些理想特性。 我们进一步在 CIFAR100-20、CIFAR100-100 和 Tiny-ImageNet200 等具有大量类和不平衡类的数据集上进行实验,表明所提出的方法实现了最先进的性能。
1.1 与NMCE的区别
最近的NMCE也提出了我们研究的同一问题的解决方案,即对数据进行聚类并学习正交子空间表示的并集。特别地,NMCE在表示和成员矩阵上优化MCR2。在本文中,我们采用了类似的公式,使用双随机矩阵对点对affinity进行建模。除了有不同的概念公式和算法外,我们的公式在初始化方面更稳定,自然适用于分层聚类。
2. Problem Formulation
在这里,我们的方法基于MCR 2 ^2 2的原理,该原理旨在当给定membership y y y时的有监督情况下学习理想表示。然后,我们讨论了同时进行聚类和学习表示的挑战,并提出了我们的聚类目标来解决该问题。
2.1. Supervised Manifold Linearizing via MCR 2 ^2 2
令为 f θ : R D → S d − 1 f_\theta:\mathbb R^D\rightarrow \mathbb S^{d-1} fθ:RD→Sd−1为由神经网络重参数化的featurizer,输出的特征为 Z θ : = [ z 1 , . . . , z n ] = [ f θ ( x 1 ) , . . . , f θ ( x n ) ] ∈ R d × n Z_\theta:=[z_1,...,z_n]=[f_\theta(x_1),...,f_\theta(x_n)]\in\mathbb R^{d\times n} Zθ:=[z1,...,zn]=[fθ(x1),...,fθ(xn)]∈Rd×n,MCR 2 ^2 2优化以下目标得到理想的表示:
max
θ
R
(
Z
θ
;
ϵ
)
−
R
c
(
Z
θ
,
Π
;
ϵ
)
s
.
t
.
Z
θ
∈
S
\max_\theta R(Z_\theta;\epsilon)-R_c(Z_\theta,\Pi;\epsilon)\quad s.t. \ Z_\theta\in\mathcal S
θmaxR(Zθ;ϵ)−Rc(Zθ,Π;ϵ)s.t. Zθ∈S
R
(
Z
θ
;
ϵ
)
=
log
det
(
I
−
d
n
ϵ
2
Z
θ
Z
θ
⊤
)
R_(Z_\theta;\epsilon)=\log\det(I-\frac{d}{n\epsilon^2}Z_\theta Z_\theta^\top)
R(Zθ;ϵ)=logdet(I−nϵ2dZθZθ⊤)
R
c
(
Z
θ
,
Π
;
ϵ
)
=
∑
j
=
1
k
⟨
Π
j
,
1
⟩
n
log
det
(
I
+
d
⟨
Π
j
,
1
⟩
ϵ
Z
θ
D
i
a
g
(
Π
j
)
Z
θ
⊤
)
R_c(Z_\theta ,\Pi ;\epsilon)=\sum_{j=1}^k\frac{\langle\Pi_j,\textbf 1\rangle}{n}\log\det\left(I+\frac{d}{\langle\Pi_j,\textbf 1\rangle\epsilon}Z_\theta \mathrm{Diag}(\Pi_j)Z_\theta^\top \right)
Rc(Zθ,Π;ϵ)=j=1∑kn⟨Πj,1⟩logdet(I+⟨Πj,1⟩ϵdZθDiag(Πj)Zθ⊤)
其中 S \mathcal S S表示被normalization layer进行 ℓ 2 \ell_2 ℓ2规范化空间。 Π ∈ R n × k \Pi\in\R^{n\times k} Π∈Rn×k为成员矩阵, Π j \Pi_j Πj为其第j列,因此 ⟨ Π j , 1 ⟩ \langle\Pi_j,\textbf 1\rangle ⟨Πj,1⟩表示属于第j类的数据点数目, ϵ \epsilon ϵ为精度超参。
当正确的 Π \Pi Π给定时,优化MCR 2 ^2 2目标可以得到每个类簇均匀分布于一个子空间中(类内丰富)且不同类簇之间正交(类间可区分)。
2.2. Unsupervised Manifold Linearizing and Clustering via MCR 2 ^2 2
在这里,我们考虑将MCR 2 ^2 2用于无监督的情况。因此需要同时优化 θ \theta θ和 Π \Pi Π。然而,这通常是组合优化问题:其复杂性在呈 n n n和 k k k的指数级增长,并且不允许的平滑和渐进变化。此外,第二个挑战是鸡和蛋的问题:如果已经有了理想的表示,那么可以应用现有的子空间聚类方法来估计membership;同样,如果已经有membership,那么求解MCR 2 ^2 2将得到理想的表示。
双随机子空间聚类
在子空间聚类中,人们通常不会直接学习隶属关系的
n
×
k
n\times k
n×k矩阵。 相反,我们首先学习表示点对之间相似性的affinity矩阵,然后对学习到的内容应用谱聚类以获得最终聚类。 此外,对affinity进行双随机约束,抑制的错误连接以获得最先进的经验性能。受此启发,我们的约束写为:
Ω
=
{
Π
∈
R
n
×
n
:
Π
≥
0
,
Π
1
=
Π
⊤
1
}
\Omega = \{\Pi\in\R^{n\times n}:\Pi\geq0,\Pi\textbf 1=\Pi^\top\textbf 1\}
Ω={Π∈Rn×n:Π≥0,Π1=Π⊤1}
然而,仅此约束不足以实现强大的聚类性能:仅考虑关于 $\Pi$ 的优化,并注意目标关于$\Pi$是强凸的。 由于我们最大化关于凸约束的凸函数,最优的
Π
\Pi
Π将位于
Ω
\Omega
Ω的极值点,对于双随机矩阵是置换矩阵。 这对于聚类来说并不理想,因为它意味着每个点都被分配到它自己独特的类,并且没有动机将点合并到更大的类簇中。 为了解决这个问题,我们添加
ℓ
2
\ell_2
ℓ2正则化鼓励
Π
\Pi
Π偏向均匀矩阵
1
n
1
1
⊤
\frac{1}{n}\bf 11^\top
n111⊤,通过调整正则化项的权重我们还可以调整
Π
\Pi
Π的稀疏度。 这得到了我们最终提出的MLC:
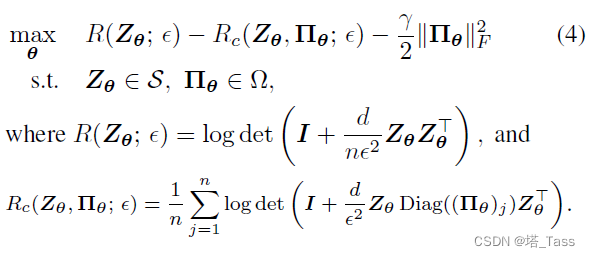
Π
θ
\Pi_\theta
Πθ现在同样由神经网络重参数化。我们首先展示该优化目标的几个优点:
- 参数化为神经网络使用固定的参数,每个mini-batch仅需占用batch size的内存和计算复杂度,而维护自由变量需要占用 n × n n\times n n×n的内存。
- 与NMCE相比,NMCE直接参数化membership,即对该矩阵 Π n × k \Pi_{n\times k} Πn×k建模。 Π n × k \Pi_{n\times k} Πn×k的初始化是任意的,与初始化表示中的结构无关, Π n × k \Pi_{n\times k} Πn×k的错误初始化可能导致来自不同真实簇的特征被压缩,因此NMCE不得不分开训练并需要三个阶段。 另一方面,可以使用来自自监督初始化特征 Z的结构确定地初始化双重随机membership。此外,有趣的是,我们的优化目标允许解释将每个点与其相邻点线性化。
2.3 Algorithms
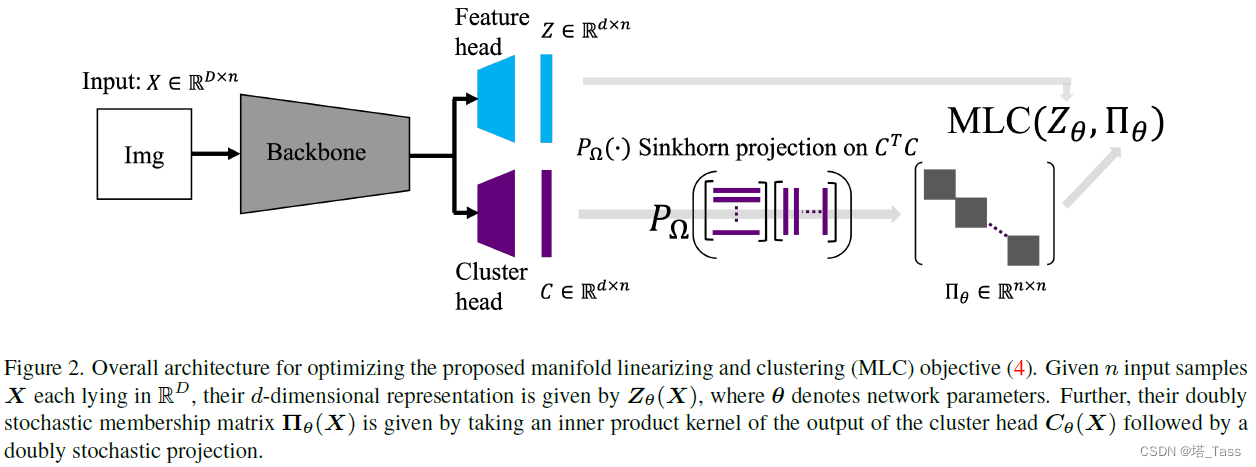
参数化 Z θ Z_\theta Zθ
我们附加了一些具有非线性的仿射层作为表示头,以转换为 R d \R^{d} Rd的输出,然后是一个normalization层以满足 Π ∈ S d − 1 \Pi\in \mathcal S_{d-1} Π∈Sd−1约束。
参数化 Π θ \Pi_\theta Πθ
在子空间聚类中,给定数据 X 的 Π \Pi Π通常采用 g ( X ) ⊤ g ( X ) g(X)^\top g(X) g(X)⊤g(X) 的形式, g g g为某种线性变换。例如在内积核函数中, g = I g=I g=I ;最小二乘回归中 g = ( I + λ X ⊤ X ) − 1 / 2 g=(I+\lambda X^\top X)^{-1/2} g=(I+λX⊤X)−1/2。 这促使我们通过神经网络对 g g g进行参数化,并将 C θ ⊤ C θ ∈ R n × n C_\theta^\top C_\theta\in\R^{n\times n} Cθ⊤Cθ∈Rn×n 作为membership,其中 C θ = g ( X ) C_\theta=g(X) Cθ=g(X)就是图中的cluster head。 然而,这样的 n × n n\times n n×n矩阵通常不是双随机的,因此我们使用了Sinkhorn投影层以获得最终结果 P Ω , η ( C θ ⊤ C θ ) ∈ Ω P_{\Omega,\eta}\left(C_\theta^\top C_\theta\right)\in\Omega PΩ,η(Cθ⊤Cθ)∈Ω。
[1] A unified framework for implicit sinkhorn differentiation. In IEEE/CVF Conference on Computer Vision and Pattern Recognition 2022.
[2] Transformers with doubly stochastic attention. In International Conference on Artificial Intelligence and Statistics, Oct. 2021.
初始化 Z θ Z_\theta Zθ:通过自监督表示学习
正确初始化
Z
Z
Z与
Π
\Pi
Π对收敛到良好的局部最优非常重要。 另一方面,随机初始化的特征通常远非理想, 因此我们采用和NMCE一样的自监督策略,即要求增广样本之间相互接近:
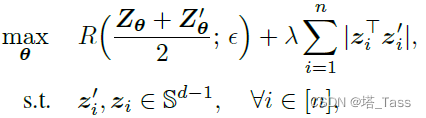
初始化 Π θ \Pi_\theta Πθ
在上述自监督特征初始化之后, Z Z Z已经有了一些我们可以利用的结构。因此,我们建议将 Π θ \Pi_\theta Πθ初始化为 P Ω , η ( Z θ ⊤ Z θ ) ∈ Ω P_{\Omega,\eta}\left(Z_\theta^\top Z_\theta\right)\in\Omega PΩ,η(Zθ⊤Zθ)∈Ω,这很容易通过在前者的自监督初始化后将 Z θ Z_\theta Zθ的参数从复制到Cluster head C θ C_\theta Cθ来实现。
最终的算法1:

所以MLC的cluster head不像NMCE那样能直接展示所属关系,而需要谱聚类这样不稳定不可微的方法。不过NMCE的cluster head也有自己的问题,比如merge acc和标准acc差距过大。
2.4 与子空间聚类的比较
为了证明MLC对样本进行聚类和流形线性化的能力,我们在CIFAR10上进行了实验。子空间聚类方法主要依赖于数据接近线性子空间并集的假设,而许多真实世界的数据集可能无法满足这一假设。为了证明这一点,我们还将所提出的方法与子空间聚类方法进行了比较。将子空间聚类直接应用于CIFAR10的自监督特征将产生较低的聚类精度。相反,MLC能够实现高的聚类精度,并且产生正交子空间表示的并集,在该并集上,子空间聚类方法也可以实现高精度。
3 Experiments
略

![[ 高并发]Java高并发编程系列第二篇--线程同步](https://img-blog.csdnimg.cn/img_convert/c6b8f3f7c738d69fbd794ae6997f7a30.png)



![迭代器设计模式(Iterator Design Pattern)[论点:概念、组成角色、相关图示、示例代码、框架中的运用、适用场景]](https://img-blog.csdnimg.cn/20e2f2a9584e413cb950f50070dc8213.png)