一、贪心算法
1、定义
贪心算法(贪婪算法)是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所作出的是在某种意义上的局部最优解。
贪心算法并不保证会得到最优解，但是在某些问题上贪心算法的解就是最优解。要会判断一个问题能否用贪心算法来计算。
2、找零问题求解
（1）问题
假设商店老板需要找零n元钱，钱币的面额有：100元、50元、20元、5元、1元，如何找零使得所需钱币的数量最少？
（2）求解思路
根据当前最优解，因此首先找到最大面值的钱币张数，可以使需要找零的张数最少，再依次递减到面值小的钱币，进行找零。例如，找零376元，先用100元找，需要3张；再用50元找，可以找1张，然后用20元找，可以找1张，之后用5元找，可以找1张，剩余的用1元找，需要1张。
（3）代码实现
t = [100,50,20,5,1] # 手上的钱,倒序排列
def change(t, n): # n是找零的钱数
m = [0 for _ in range(len(t))] # 找零张数
for i,money in enumerate(t): # i是列表索引，money是索引对应的值
m[i] = n // money # m列表的第i个值，是找零的钱除以钱币的面值
n = n % money # 剩余需找零的钱是取余
return m,n # 找零张数列表，以及找不开的张数
print(change(t, 376))输出结果：
([3, 1, 1, 1, 1], 0)二、背包问题-贪心算法求解
1、背包问题
（1）问题背景
一个小偷在某个商店发现有n个商品，第i个商品价值vi，重wi千克。他希望拿走的价值尽量高，但他的背包最多只能容纳W千克的东西。他应该拿走哪些商品？
（2）背包问题分类
1）0-1背包：对于一个商品，小偷要么把它完整的拿走，要么留下。不能只拿走一部分，或把一个商品拿走多次。（例如：商品为金条）
2）分数背包：对于一个商品，小偷可以拿走其中任意一部分。（例如商品为金砂）
（3）背包问题分析
对于0-1背包和分数背包，贪心算法是否都能得到最优解?为什么?
结论：0-1背包不可以，分数背包可以。
说明：
分数背包可以拿走商品的一部分，根据贪心算法原则可以从最值钱的开始装，将整个背包的空间全部利用完。例如：装金砂和银砂，先装满金砂，有空余的位置再装银砂，直到背包装满。
0-1背包不能拿走一部分商品，必须将商品全部拿走。例如：下面问题：
商品1：v1=60 ，w1=10
商品2∶v2=100 ，w2=20
商品3∶v3=120， w3=30
背包容量:W=50
按照贪心算法的原则，先拿走单价最贵的商品，商品1>商品2>商品3，因此会先装商品1，再装商品2，此时剩余空间为20，无法装下商品3，能够带走的总价值为160。然而最优解应该是带走商品2和商品3，容量刚好为50，且价值为220。
2、分数背包——贪心算法实现
（1）问题实例
分数背包问题，商品可以带走部分。
商品1：v1=60 ，w1=10
商品2∶v2=100 ，w2=20
商品3∶v3=120， w3=30
背包容量:W=50
（2）代码实现
goods = [(60,10),(120,30),(100,20)] # 每个元组代表（价值，重量），也可以用字典表示
goods.sort(key= lambda x : x[0] / x[1], reverse= True) # 根据商品单价降序排序
print(goods)
def fractional_backpack(goods, w): # goods是列表降序排序后，w表示背包容量
m = [0 for i in range(len(goods))] # 表示各商品可装的数量
total_v = 0 # 总价值
# 循环-根据贪心算法原则，求解
for i, (price, weight) in enumerate(goods):
if w >= weight: # 背包空间可以带走整个商品
m[i] = 1 # 商品整个带走
w = w - weight # 剩余背包容量
total_v += price # 商品价值相加
else: # w<weight, 无法将整个商品带走，只能装下一部分
m[i] = w / weight # 可带走部分
w = 0 # 背包容量用完
total_v += price * m[i] # 商品总价值 * 带走的商品数量
break # 跳出循环
return total_v, m
print(fractional_backpack(goods, 50))结果输出：
[(60, 10), (100, 20), (120, 30)]
(240.0, [1, 1, 0.6666666666666666])三、数字拼接问题-贪心算法
问题（p83）
（1）问题概述
有n个非负整数,将其按照字符串拼接的方式拼接为一个整数。如何拼接可以使得得到的整数最大?
例如：32,94,128,1286,6,71可以拼接除的最大整数为94716321286128。
（2）实现理论
虽然可以根据字符串的首个字符大小，再排序，使用贪心算法原则。但是存在数字大小类似的情况，例如，128,1286。通过例如，a= 128，b=1286，对比a+b和b+a的大小，确定怎么排序，得到最后的值更大。
2、代码实现
（1）知识点-函数语法
str()函数：参数转换成字符串类型。
a = 12
b = str(a)
print(b)
#input
"12"map()函数：会根据提供的函数对指定序列做映射。第一个参数 function 以参数序列中的每一个元素调用 function 函数，返回包含每次 function 函数返回值。
语法：map(function, iterable, ...)，function -- 函数，iterable -- 一个或多个序列。
# input
def add(a,b):
return a + b
a = [1,3,5,7]
b = [2,4,6,8]
x = map(add,a,b)
y = list(map(add,a,b))
print(x)
print(y)
# output
<map object at 0x0000020BD5404F70>
[3, 7, 11, 15]join()函数：用于将序列中的元素以指定的字符连接生成一个新的字符串。
语法：str.join(sequence)，sequence -- 要连接的元素序列。
# input
li = [32, 94, 128, 1286, 6, 71]
seq = list(map(str,li))
seq_join = "*".join(seq) # 用*号连接字符串
print(seq_join)
#output
32*94*128*1286*6*71functools模块中的cmp_to_key部分
作用：两个传入参数x,y 当x>y时返回1 等于时返回0，否则返回-1。它在list中的工作机制就是将列表中的元素去两两比较，当cmp返回是正数时交换两元素。在list中表现为排序。
# 输入
from functools import cmp_to_key # 排序模块
li = [32, 94, 128, 1286, 6, 71]
def cmp_rise(a,b):
'''
升序排序：
当前面的参数a小于后面的参数b返回-1，-1代表保持不变，
当前面的的参数a大于等于后面的参数b返回1，1代表交换顺序。
保证前面的数字小于后面的数字
'''
if a < b:
return -1
else:
return 1
x_sorted_by_rise = sorted(li,key=cmp_to_key(cmp_rise))
print(x_sorted_by_rise)
def cmp_decline(a,b):
'''
降序排序：
当前面的参数a小于后面的参数b返回1，1代表交换顺序，
当前面的的参数a大于等于后面的参数b返回-1，-1代表保持不变。
因此保证了前面的数子大于后面的数字，是降序排序。
'''
if a < b:
return 1
else:
return -1
x_sorted_by_decline = sorted(li, key = cmp_to_key(cmp_decline))
print(x_sorted_by_decline)
# 输出
[6, 32, 71, 94, 128, 1286]
[1286, 128, 94, 71, 32, 6]（2）代码实现
from functools import cmp_to_key # 排序模块
li = [32, 94, 128, 1286, 6, 71]
# 根据贪心算法，将数字字符串相连后更大的数字交换位置，后拼接。
# 降序排序，原理在知识点已解析
def xy_cmp(a,b):
if a + b < b + a: # 交换位置
return 1
else:
return -1 # 不交换位置
def number_join(li): # 数字拼接
li = list(map(str, li)) # 转换为字符串
li.sort(key=cmp_to_key(xy_cmp)) # 按xy_cmp函数的排列要求排序
return "".join(li) # 拍好序后的列表拼接
print(number_join(li))输出结果：
94716321286128四、活动选择问题-贪心算法（p85-86）
1、活动选择问题
（1）问题概述
假设有n个活动，这些活动要占用同一片场地，而场地在某时刻只能供—个活动使用。
每个活动都有一个开始时间s和结束时间f(题目中时间以整数表示),表示活动在[si, fi)区间占用场地。
问:安排哪些活动能够使该场地举办的活动的个数最多?
（2）贪心原则
1）结论：最先结束的活动一定是最优解的一部分。
2）证明:
假设a是所有活动中最先结束的活动， b是最优解中最先结束的活动。
如果a=b，结论成立。
如果a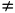
b，则b的结束时间一定晚于a的结束时间，则此时用a替换掉最优解中的b, a一定不与最优解中的其他活动时间重叠，因此替换后的解也是最优解。
2、代码实现
activities = [(0, 6), (5, 7), (3, 9), (1, 4), (3, 5), (5, 9),
(6, 10), (2,14), (12, 16), (8, 11), (8, 12)] # 元组列表表示(si,fi)
# 根据贪心算法结论，按最早结束时间排序
activities.sort(key = lambda x: x[1]) # 这里的x是列表中每个元组，lambda求得x[1],元组中的第二个数
def activities_selection(a): # param a：活动列表
res = [a[0]] # 结果列表，活动列表中最先结束活动的一定也说最优解中最先结束的活动
for i in range(1,len(a)): # a[0]已经传入结果列表
# 保证开始时间与上一个活动结束时间不重叠
if a[i][0] >= res[-1][1]: # 第i个活动的开始时间：a[i][0];上一个活动（最优解中）的结束时间：res[-1][1]
res.append(a[i])
return res
print(activities_selection(activities))输出结果：
[(1, 4), (5, 7), (8, 11), (12, 16)]五、贪心算法总结
用于求解最优化问题，速度较快，代码相对简单。
不是所有的最优化问题都能用贪心算法求解，例如，0-1背包问题。
