分享本文在朋友圈的读者可获得本文数据和 Python 代码。留个言说已分享(不用截屏)我相信你,我会发给你百度盘下载链接。
本文长度为 6393 字,建议阅读 32 分钟
题图:SignalPlus Dashboard
0
引言
Deribit volatility (DVOL) 指数是 Deribit 制定的加密货币期权的波动率指数,它衡量的是 30 天的向前看 (forward-looking) 预期波动率 (implied volatility 从期权价格隐含计算出来),而不是向后看 (backward-looking) 实际波动率 (realized volatility 从标的价格时间序列计算)。
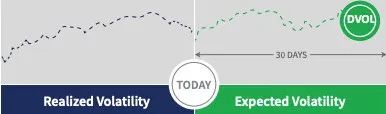
DVOL 是一个年化波动率的预期。粗略来讲,要获得 BTC 价格每日的预期变动,只需将 DVOL 值除以 19 (365 的平方根) 即可。 例如,DVOL 等于 57 (其实指的是 57%) 相当于 3% 的日波动。
和老规矩一样,在前戏王中我会介绍推导所需要的知识点;在理论皇中我会根据不同市场惯例给出不同的波动率指数表达式,如股票市场的 VIX 和币圈市场的 DVOL;在实践狼中我会讲解如何用 Python 来计算 DVOL。
LET'S GO!
1
前戏王
1.1
方差期望
假设标的资产的 SDE 和经过伊藤定理变形后的 SDE 如下:
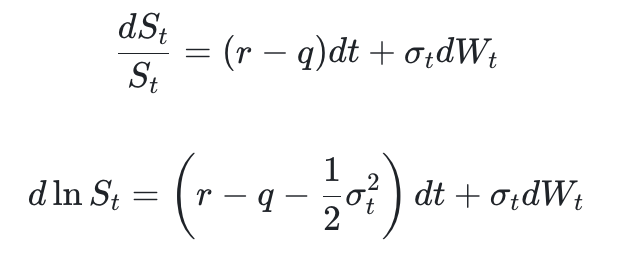
第 2 个公式减去第 1 个公式后,两边乘以 2 得到:
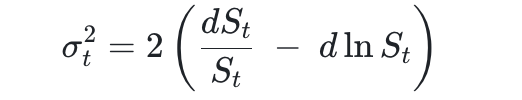
两边从 0 到 T 求积分得到:
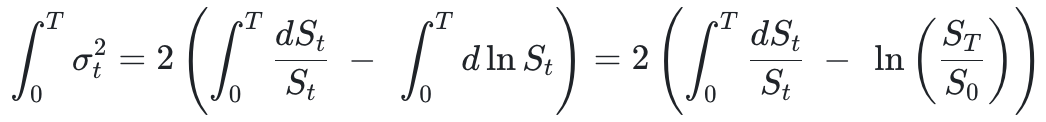
两边求期望得到:
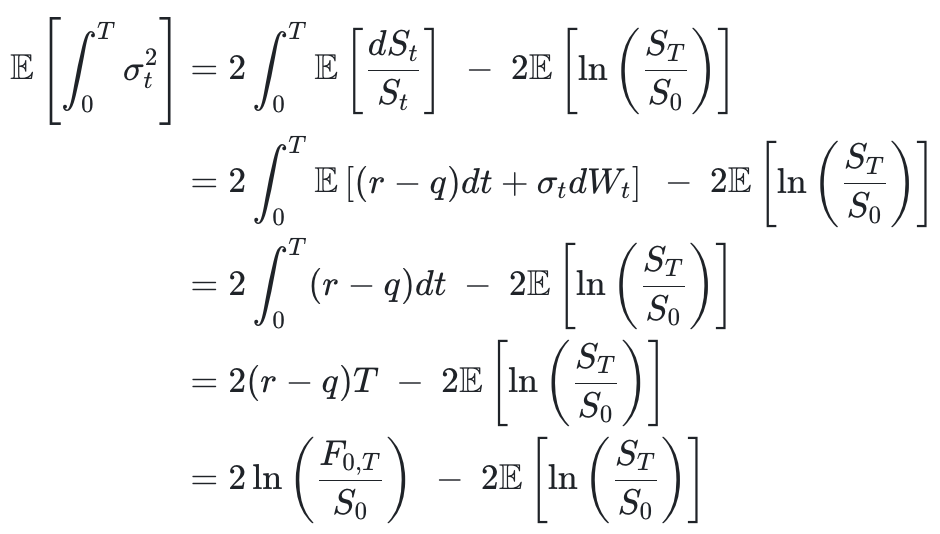
上式中的 F0,T 是标的资产在 T 时到期的远期价格,而左边的期望值年化后 (除以 T) 就是方差,即
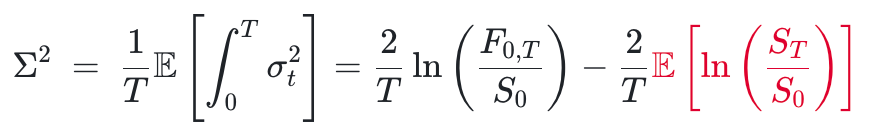
1.2
Carr & Madan 公式
Carr & Madan 公式是本文证明需要的核心内容,公式如下:
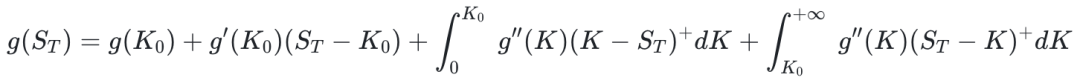
该公式咋一看很复杂,实际上就是利用了泰勒展开。在实操时,可把 g(ST) 看成某个金融产品的支付函数,右边积分项里有 put 和 call 的支付函数,这样对于任何一个金融产品,其支付函数都可以用一系列的 put 和 call 来合成。
为了推导波动率指数,我们选取对数合约作为这个金融产品。
推导见 https://gregorygundersen.com/blog/2023/01/26/carr-madan/。
1.3
对数合约
对数合约 (log contract) 是一种奇异期权 (exotic option),它根据其标的资产价格的对数进行支付。对数合约的收益是单一资产价格的非线性函数。这种类型的期权使投资者表达对未来波动的看法。
给定对数合约的支付函数 g(x) = ln(x/S*),其一阶导数和二阶导数为
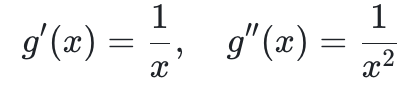
注意到小节 1.1 最后得到公式里红色那一项就是对数合约的期望,利用对数性质 ln(ab) = ln(a) + ln(b) 做以下的恒等变换:
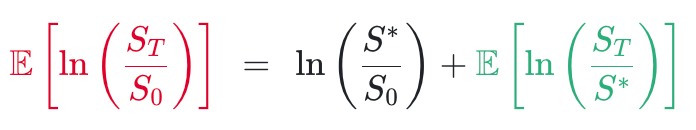
代入 Carr & Madan 公式得到
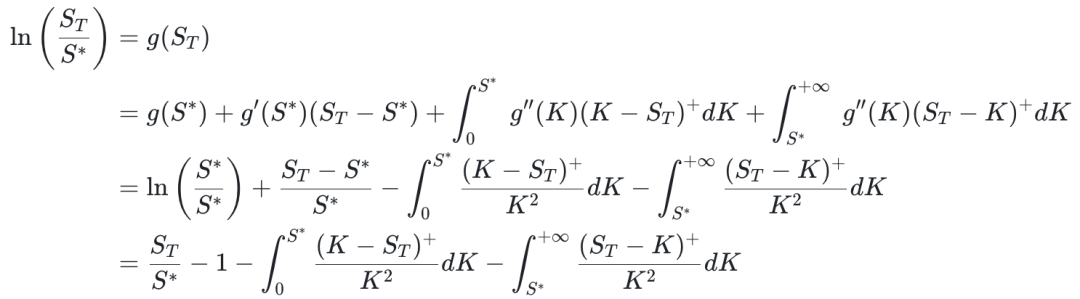
两边求期望可计算出
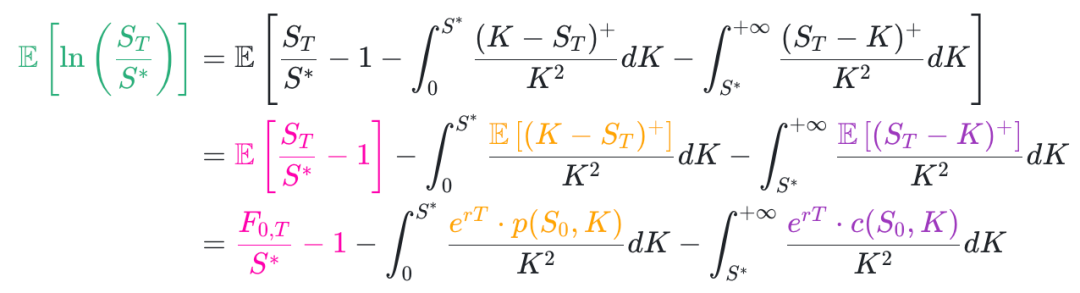
将上面结果代入对数合约得到,
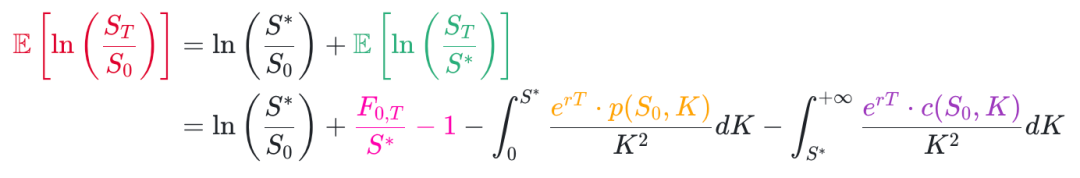
将对数合约推导结果代入方差表达式得到,
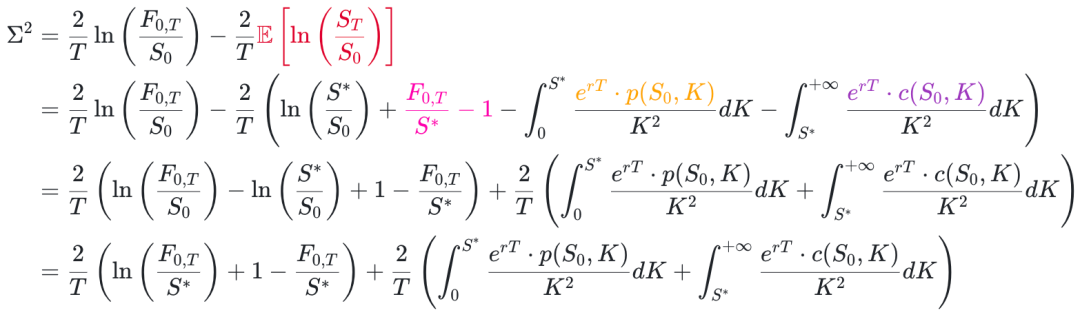
这个公式就是方差的期望的精确数学表达式。
2
理论皇
根据上节最后一个公式根据不同资产市场的惯例做一些调整就能得到股票市场上的 VIX 公式和加密货币市场的 DVOL 公式。
2.1
VIX 公式
上节最后一个公式的推导和模型无关 (model-independent)
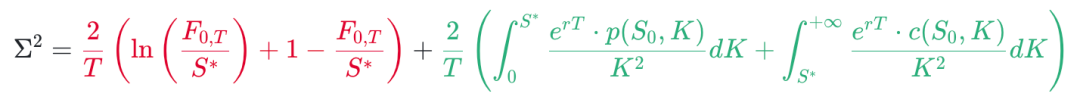
但是用在实操上,还需要做几个近似:
首先远期价格 F0,T 是通过先找到最接近价中 (at-the-money, ATM) 的看涨期权 c0 和看跌期权 p0,再用平价公式 (put-call parity) 计算出来的:
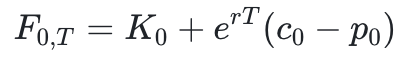
红色的项可根据当 x ≈ 0 有 ln(1+x) ≈ x - 0.5x2 做进一步的化简
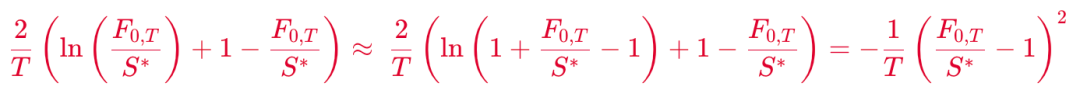
在实操时,通常 S* 选一个离 F0,T 很近但是小于它的值,那么 1 - F0,T/S* 是一个很接近 0 的数,因此上面的近似关系成立。
绿色的项可用累加近似积分
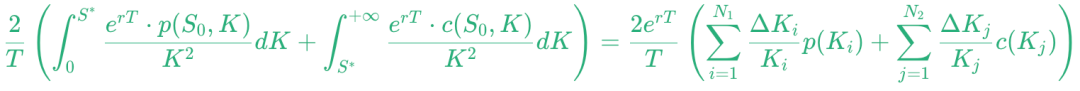
由于 S* ≈ F0,T ,那么上式中的看跌期权 p(Ki), Ki ≤ F0,T 和看涨期权 c(Kj), Kj ≥ F0,T 都是价外期权 (out-of-the-money, OTM)。这样可操作的 VIX 指数表达式为
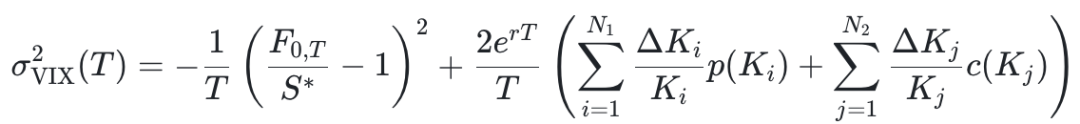
实际上 VIX 是衡量 30 天的波动率的指标,因此会根据离 30 天最近的两个到期日的期权计算出 σ2VIX(T1) 和 σ2VIX(T2),再做一个线性插值,
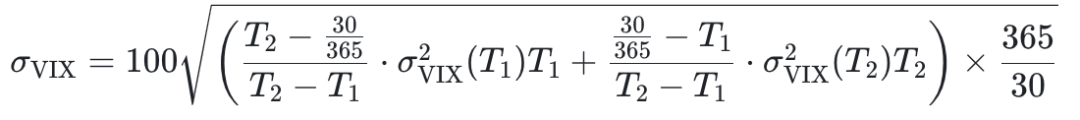
2.2
DVOL 公式
DVOL 是 Deribit 发布的关于加密货币的波动率指数,Deribit 上面的期权有两大特征:
-
期权是币本位而不是 U 本位
标的是期货价格而不是现货价格
根据上述两个特征我们需要更改两处地方
1. 计算远期价格 F0,T 的公式需要改,因为期权是币本位,因此需要用 F0,T 转换成 U 本位,而且去掉 r,公式改成
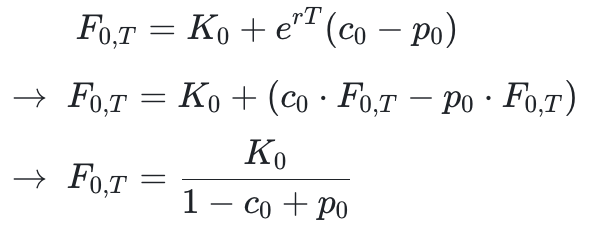
这个和 Deribit 官网上 DVOL 白皮书的公式吻合:

2. 计算 strike constribution 的地方也要改:
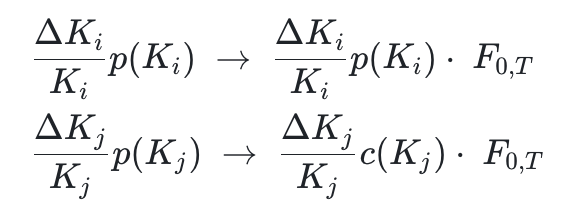
这个也和 Deribit 官网上 DVOL 白皮书的公式吻合:
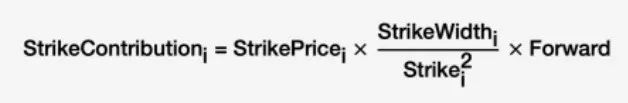
最终方差的公式变成
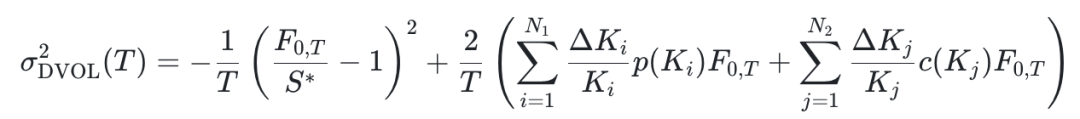
同理 DVOL 是衡量 30 天的波动率的指标,因此会根据离 30 天最近的两个到期日的期权计算出 σ2DVOL(T1) 和 σ2DVOL(T2),再做一个线性插值,
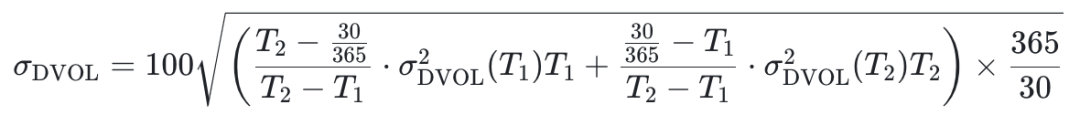
3
实践狼
3.1
数据预处理
在 31-Apr-2023 (精确时间 UTC 10:42) 时从 Deribit 上截取的离 30 天之后最近的两个到期日期权的信息。
28-Apr-2023 到期的期权信息 (28 天)
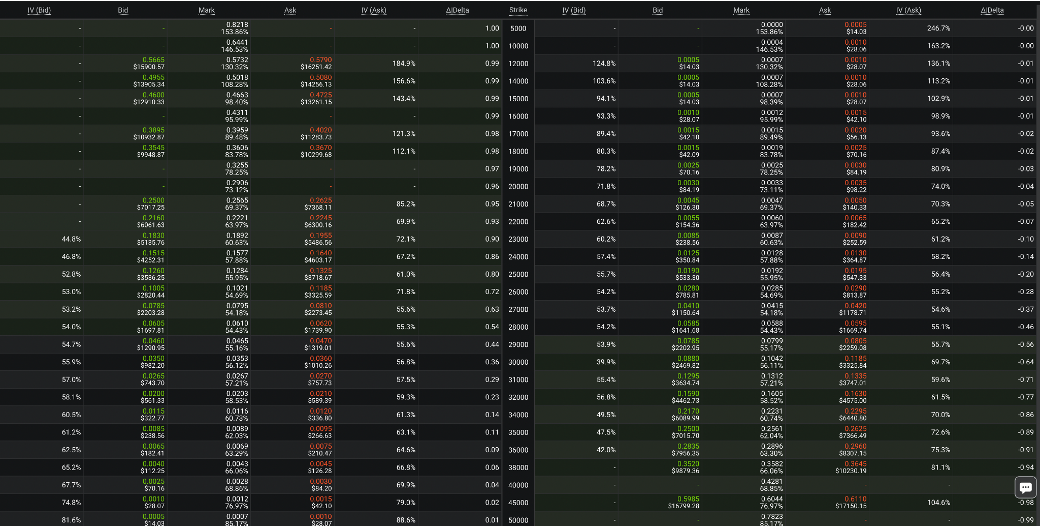
26-May-2023 到期的期权信息 (56 天)
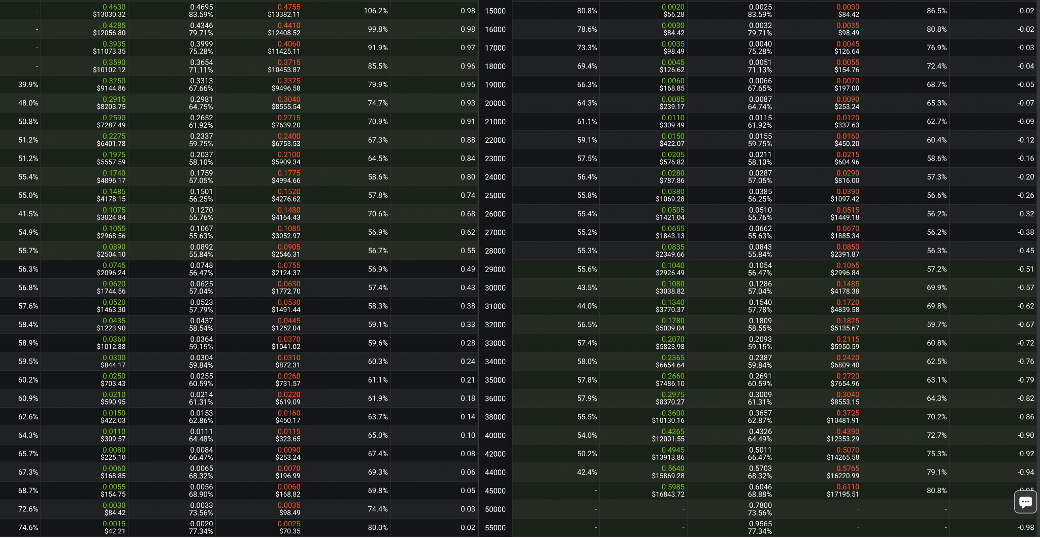
截图的数据比较乱,好消息时可以从 Deribit Options 页面上下载 csv 格式的数据,点击下图右上角的红框即可。 这样就可以下载 28-April-2023 和 26-May-2023 的数据了 (注意当你们在未来下载时,要根据当天的 30 天后来选择最近两个到期日)。

计算 DVOL 只需要不同 strike 对应 call 和 put 的 bid | mid | ask,额外还需要 delta 值来过滤数据。从上图下载的 csv 数据可处理成下图的样子。
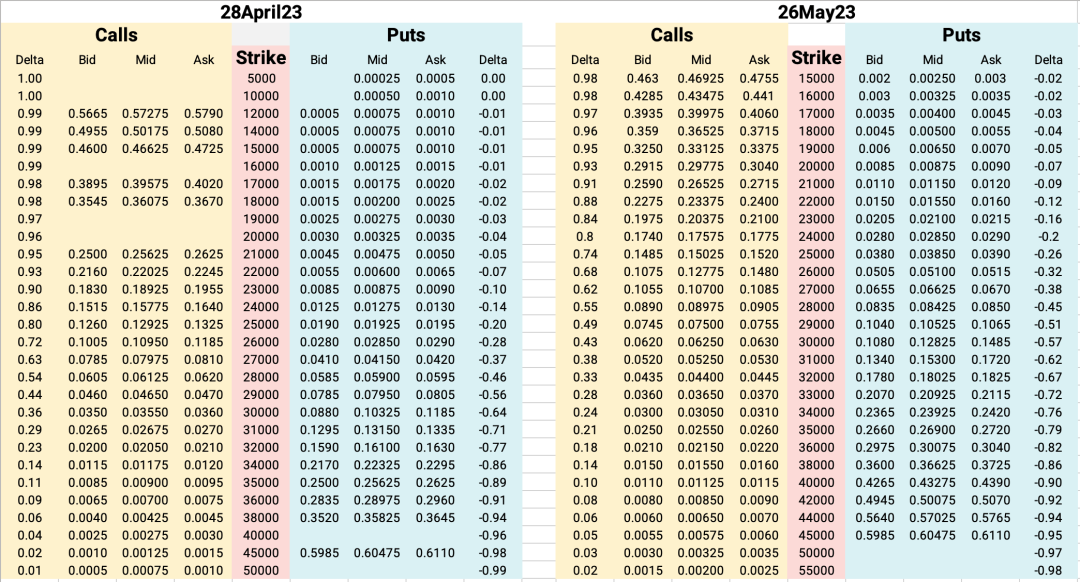
接下来用 Python 来计算 DVOL。
3.2
数据读取
首先引入需要的库 datetime, numpy 和 pandas。
from datetime import datetime
import pandas as pd
import numpy as np上图的数据已存成 excel 里的两个 sheets,用 pd.read_excel() 将 sheet_name 参数设为 None 可以读取所有 sheets 中的数据。注意 header 参数设为 [0, 1] 是为了将数据转换成两层列标签的 DataFrame。第一层列标签是 "calls", "puts";第二层列标签是 "Delta", "Bid", "Mid", "Ask"。
data = pd.read_excel( "data.xlsx", sheet_name=None,
header=[0,1], index_col=0 )
data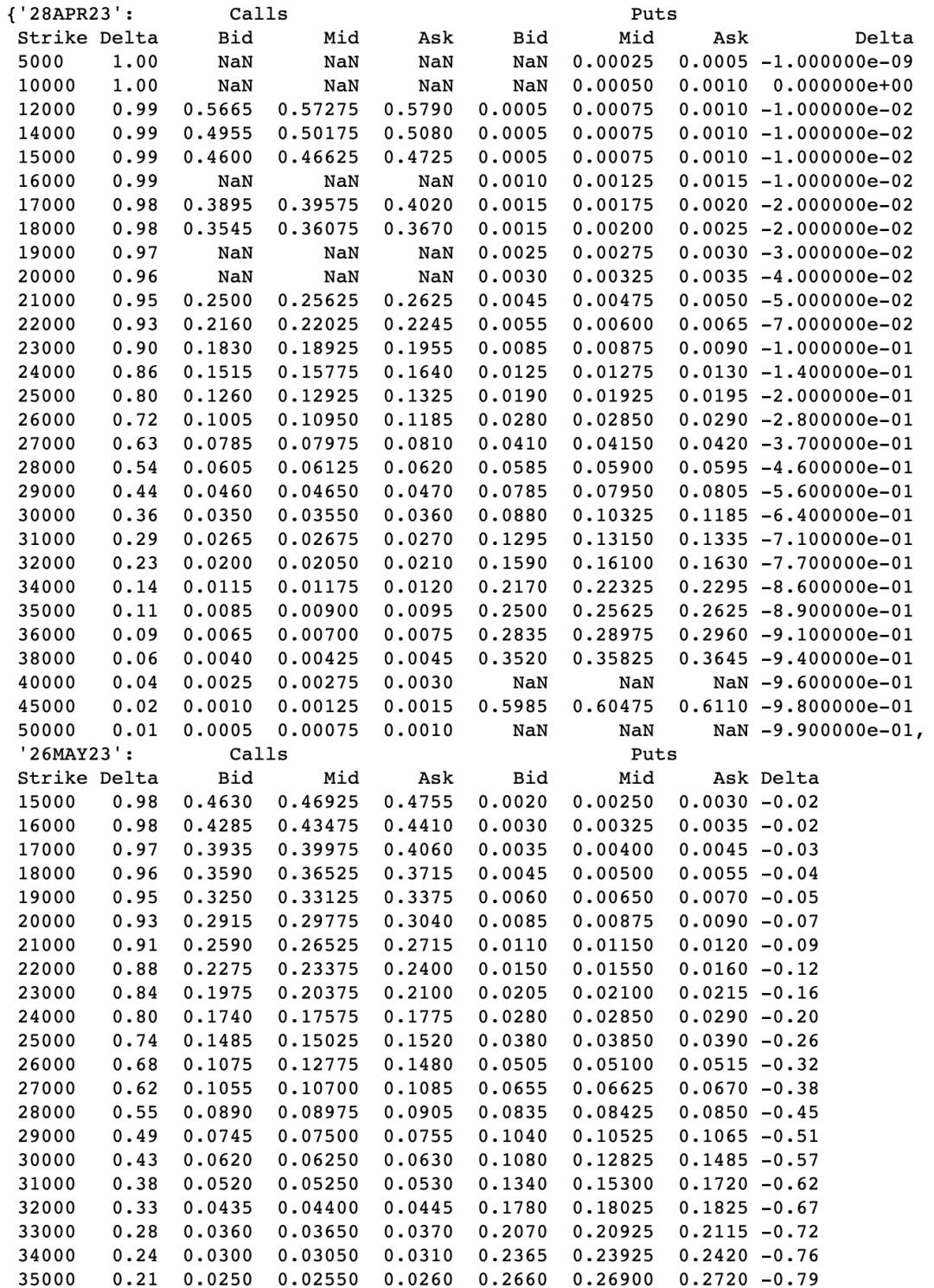
丢弃掉 delta 小于 5% 的数据,因为对应的 OTM call 和 put 的期权值太小,用它们来计算波动率会“歪曲”波动率市场深度。
写一个 cutoff() 函数来过滤 delta 小于 5% 的数据。
def cutoff( pdf, delta_cutoff=0.05 ):
return pdf[ (pdf["Calls"]["Delta"] >= delta_cutoff)
& (pdf["Calls"]["Delta"] <= 1-delta_cutoff) ]注意,这里 delta < 0.05 是指的 delta 绝对值,由于 call delta 为正,put delta 为负,那么就是过滤掉
-
delta 小于 0.05 的 call
delta 大于 -0.05 的 put (即 delta 大于 0.95 的 call)
过滤完的数据可视化如下图所示。
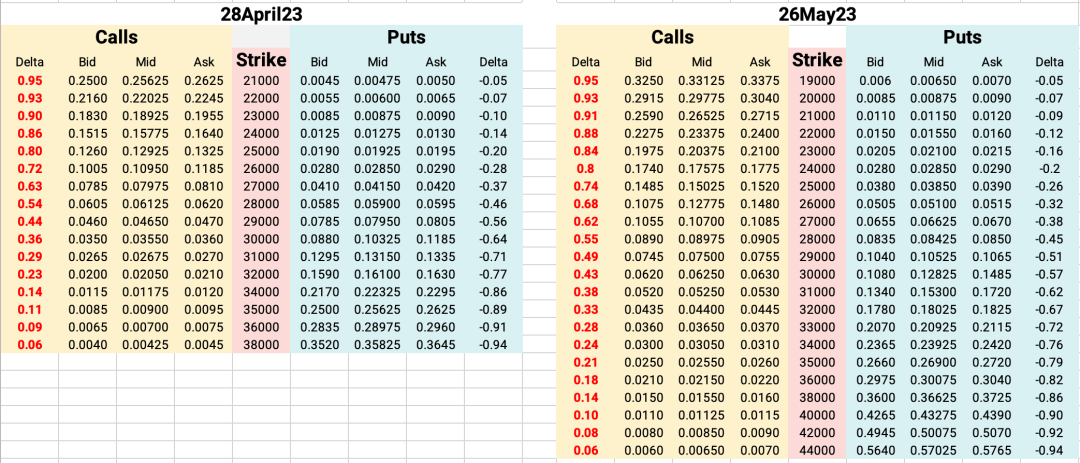
3.3
计算远期价格
根据小节 2.2,远期价格是通过先找到最接近价中 (at-the-money, ATM) 的看涨期权和看跌期权,再用平价公式 (put-call parity) 计算出来的。写一个 get_forward() 函数来实现。
def get_forward( pdf ):
abs_call_minus_put = np.abs(pdf["Calls"]["Mid"]
- pdf["Puts"]["Mid"])
idx = np.argmin(abs_call_minus_put)
call_mid = pdf["Calls"]["Mid"].iloc[idx],
put_mid = pdf["Puts"]["Mid"].iloc[idx]
strike_min = pdf.index[idx]
forward = strike_min / (1-call_mid + put_mid)
strike_cutoff = strike_min if forward > strike_min
else pdf.index[idx+1]
return strike_cutoff, forward代码解释如下:
-
第 2-3 行计算 call 和 put 的 mid 差的绝对值
第 4 行找到最小绝对值的索引
第 5-6 行根据索引找出对应的 call 和 put 作为 ATM call 和 ATM put
第 7 行根据索引找出对应的 strike 作为 ATM strike
第 8 行用平价公式计算 forward
第 9 行将最接近 forward 但比 forward 小的一个 strike 设为 strike cutoff
上述计算 forward 的过程的可视化如下图:
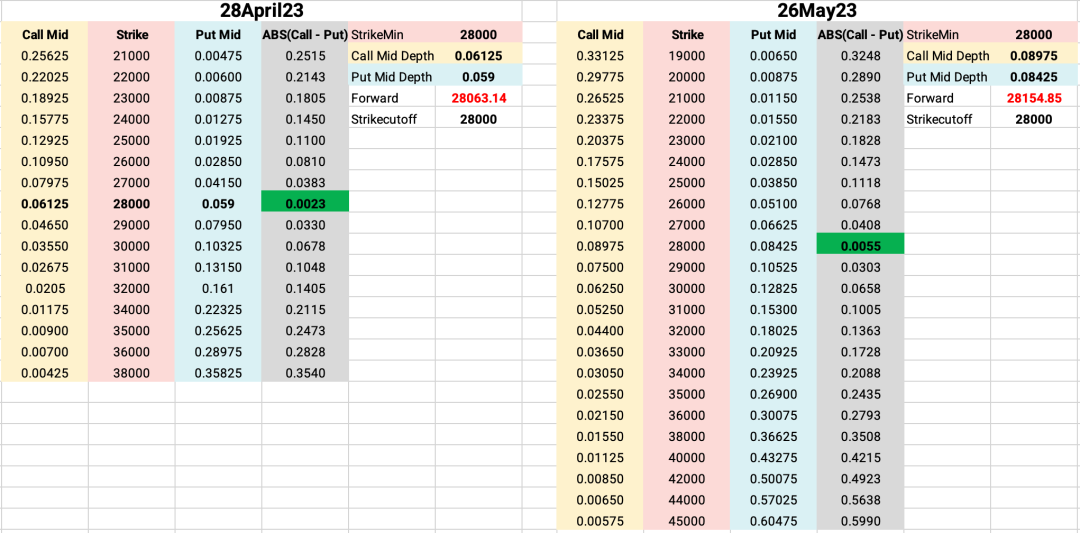
3.4
计算方差
接下来根据小节 2.2 的公式来计算方差:
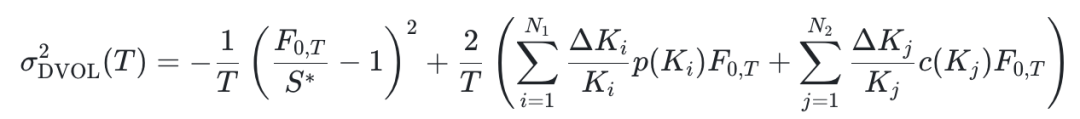
首先写一个 get_strike_width() 函数来计算公式里面的
Δ
K,公式如下:
代码很简单无需进一步的解释。
def get_strike_width( strike ):
strike_width = np.zeros(strike.shape)
strike_width[1:-1] = 0.5*(strike[2:]-strike[:-2])
strike_width[0] = strike[1] - strike[0]
strike_width[-1] = strike[-1] - strike[-2]
return strike_width接下来写一个 get_variance() 函数来实现以下公式:

def get_variance( pdf, strike_cutoff, forward, t ):
strike = pdf.index.values
strike_width = get_strike_width( strike )
otm_call = pdf["Calls"]["Mid"][strike >= strike_cutoff]
otm_put = pdf["Puts"]["Mid"][strike <= strike_cutoff]
strike_price = pd.concat([otm_put, otm_call], axis=1).mean(axis=1)
strike_contribution = strike_price * strike_width
/ (strike**2) * forward
variance = (2*strike_contribution.sum()
- (forward/strike_cutoff-1)**2) / t
return variance代码解释如下:
第 2 行获取所有 strike 数据
第 3 行用计算每个 strike 对应的行权价格的宽度
第 4-5 行利用 strike_cutoff 来找到 OTM call (舍弃所有 strike 小于 strike_cutoff 的 call) 和 OTM put (舍弃所有 strike 大于 strike_cutoff 的 put)
第 6 行将 OTM call 和 OTM put 横向拼接,并求均值,这么做的原因是在 strike cutoff 处 同时有 call 和 put,因此求一个均值当作期权价格
第 7 行根据公式计算 strike contribution
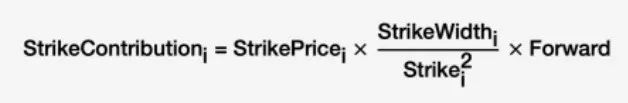
第 8 行根据公式计算 variance
上述计算 variance 的过程的可视化如下图:
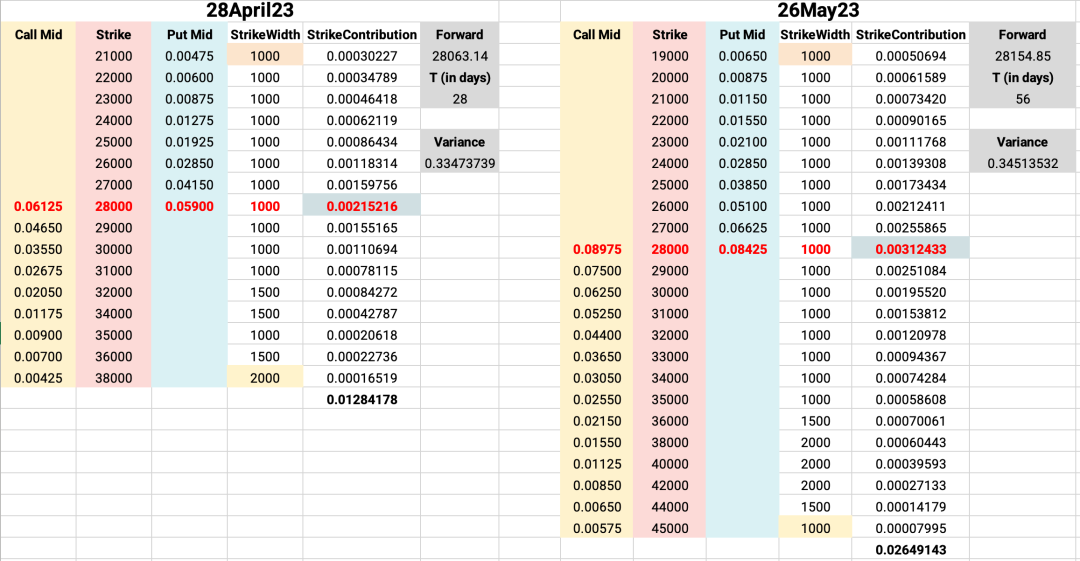
3.6
插值 DVOL
最后将所有函数放入 get_dvol() 函数中,对两个到期日的期权数据分别计算出方差,然后线性插值出 30 天的方差,最后开根号得到 DVOL。
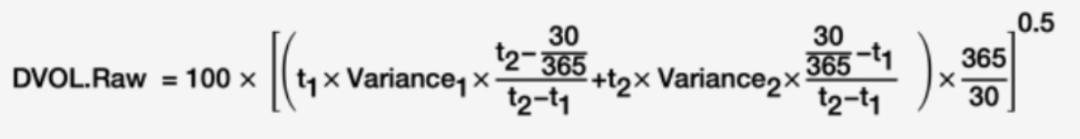
def get_dvol( data, today ):
t_list, variance_list = [], []
for expiry, df in data.items():
df = cutoff( df )
strike_cutoff, forward = get_forward( df )
t = (datetime.strptime(expiry,"%d%b%y")
- datetime.strptime(today,"%d%b%y")).days / 365
variance = get_variance( df, strike_cutoff, forward, t )
t_list.append(t)
variance_list.append(variance)
t1, t2 = t_list
v1, v2 = variance_list
dvol = ((t1*v1*(t2-30/365)/(t2-t1)
+ t2*v2*(30/365-t1)/(t2-t1)) * 365/30)**0.5
return dvol*100最后代入具体数据得到在 31-Mar-2023 计算的 DVOL 值是 57.98。
today = "31MAR23"
get_dvol(data, today)57.9761828940359插值 DVOL 过程的可视化如下:
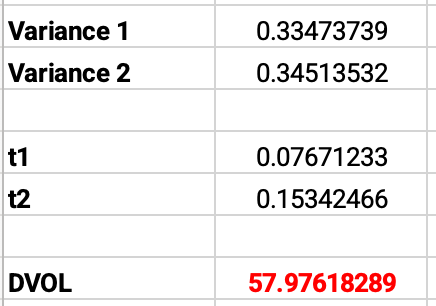
3.7
更多细节
Deribit 在计算 DVOL 时还有三个小细节需要处理:
EMA 平滑
上节计算出来的 DVOL 其实上叫 DVOL.RAW,每秒计算一次。但为了过滤噪声和平滑数据,Deribit 取最后 240 个点的指数移动平均线 (EMA) [通过调节参数 EMAPeriod] 以获得波动率指数 DVOL 的最终值。
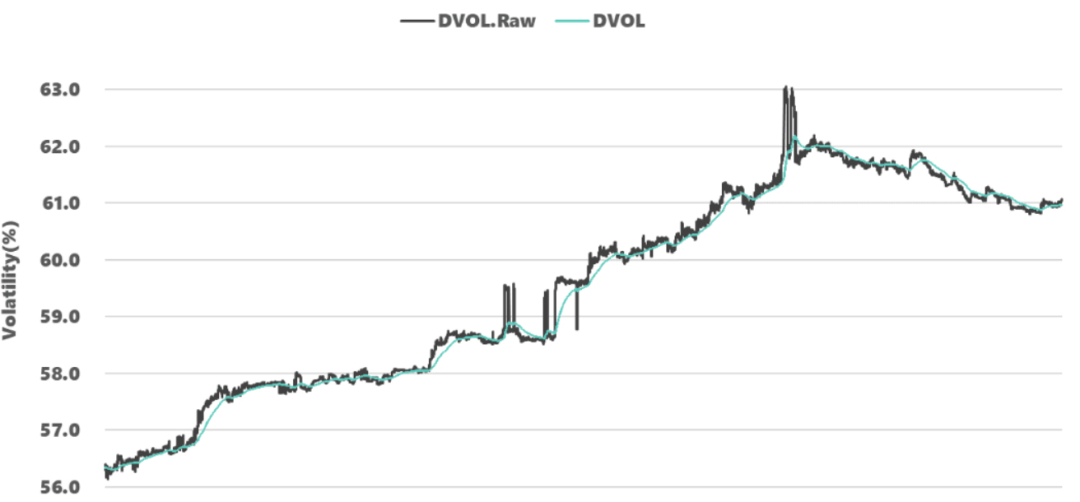
从上图不难看出,平滑后的 DVOL (淡蓝线) 比平滑前 DVOL.Raw (黑色) 少了很多 spikes。
计算 Instrument Price
我们在小节 3.1 中使用的 mid price 是已经处理好的,真正要用的 Instrument Price 还需要做下图的操作:

首先定义基差为 Depth Ask – Depth Bid,定义阈值 c = max(min(MaxSpreadBidRatio * DepthBid, MaxSpreadWidth), MinSpreadWidth)
-
当基差小于 c 时,Instrument Price 可用 Mid Depth Price 来代表。
当基差大于 c 时,Instrument Price 用 VWAP Trade Price 来代表。
如果 VWAP Trade Price 不存在,Instrument Price 用 60 秒到90 秒前的 Past Mark Price 来代表。
如果 Past Mark Price 也不存在,Instrument Price 用 Current Mark Price 来代表。
计算 Mid Depth Price
中间深度价格 = (深度卖价 + 深度买价) / 2,两者都被计算为 VWAP,直到达到至少 2 BTC [通过调节参数 DepthVolume] 的累计交易量,并总共使用 5 个层级 [通过调节参数 DepthLevels]。从第一个层级开始,每个层级只能比上一个层级相差 1 个 tick(即 0.0005 BTC)。如果这些级别的总交易量少于 2 BTC,则将在后面再创建 1 个层级,剩余的交易量为 2 BTC。具体例子如下图所示:
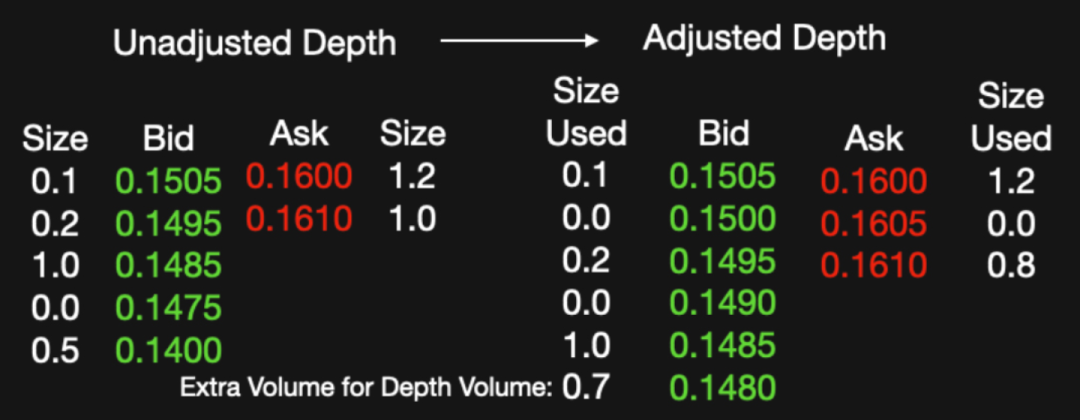
在 Bid 边,注意到加入了 0.1500 和 0.1490,因为要确保每个层级相差 0.0005 BTC。此外 0.1485 已经到第 5 层级了,累计交易量只有 1.3 BTC,因此再用 0.7 BTC 的 0.1480 来补满。 在 Ask 边,前两级累计交易量已经 2.2 BTC 了,因此补充一个 0.1605 的层级,并且在 0.1610 层级把交易量调成 0.8 BTC 使得总数为 2 BTC。
计算深度买价 Depth Bid 为

计算深度卖价 Depth Ask 为
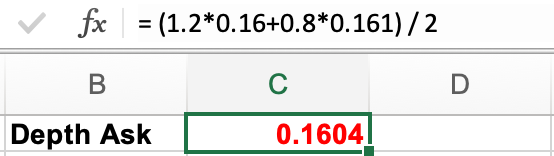
那么中间深度价格 = (深度卖价 + 深度买价) / 2 = 0.1544625。
4
总结
本文从 Carr & Madan 公式和对数合约开始,推导出方差期望的精确数学表达式,接着根据币圈的市场惯例得到 DVOL 的表达式,最后给出一套 Python 实现计算 DVOL 的流程。
以后我会分享更多和 crypto market 相关的硬核技术内容。同学们也可关注我们的官网 https://www.signalplus.com/,以及加入以下我们的社群。