选择题

2-1
我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题？

A.深度优先搜索

B.Kruskal算法

C.拓扑排序算法

D.Dijkstra算法
解析：
本题为单源最短路径问题，应选用dijsktra算法。

2-2
下图为一个AOV网，其可能的拓扑有序序列为：

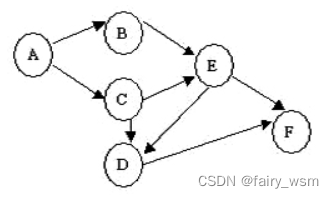
A.ABCEDF

B.ACBDEF

C.ABCDFE

D.ABCEFD
解析：
拓扑排序只输出没有入度的点，输出后删除点，从删除A开始。

2-3
任何一个带权无向连通图的最小生成树——

A.有可能不唯一

B.有可能不存在

C.是唯一的

D.是不唯一的

2-4
先序遍历图示二叉树的结果为

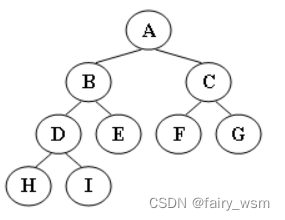
A.A，B，D，H，I，E，C，F，G

B.H，I，D，B，E，F，G，A，C

C.H，D，I，B，E，A，F，C，G

D.A，B，C，D，H，E，I，F，G
解析：
先序遍历 MLR
ABDHIECFG

2-5
设树T的度为4，其中度为1、2、3、4的结点个数分别为4、2、1、1。则T中有多少个叶子结点？

A.6

B.8

C.10

D.4
解析：
非叶子节点
4+2+1+1=8
叶子节点 x
入度之和 x+8-1
出度之和 14+22+3+4=15
出度之和等于入度之和
所以叶子节点有 x=8个

2-6
在AOE网中，什么是关键路径？

A.最短回路

B.最长回路

C.从第一个事件到最后一个事件的最短路径

D.从第一个事件到最后一个事件的最长路径

2-7
给定有向图的邻接矩阵如下：
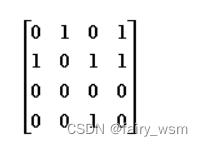顶点2（编号从0开始）的出度和入度分别是：

A.0, 2

B.2, 0

C.1, 3

D.3, 1
解析：
横为出度，纵为入度。

2-8
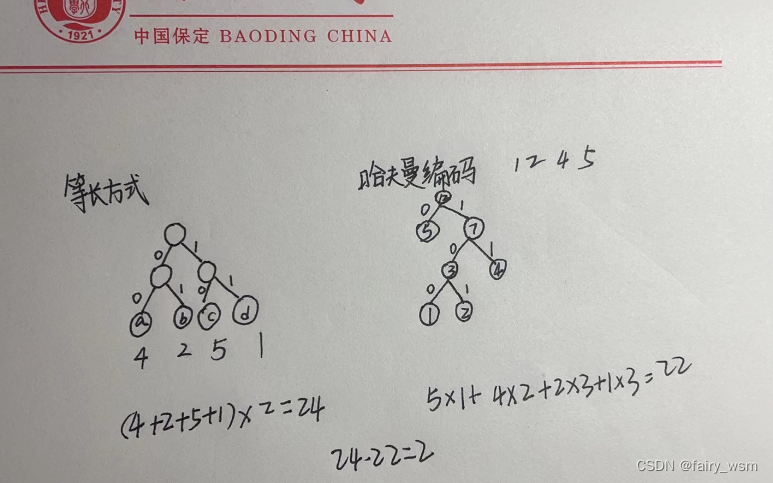
设一段文本中包含4个对象{a,b,c,d}，其出现次数相应为{4,2,5,1}，则该段文本的哈夫曼编码比采用等长方式的编码节省了多少位数？
A.0

B.5

C.4

D.2

2-9
树最适合于用来表示

A.元素之间无联系的数据

B.有序数据元素

C.元素之间具有分支层次关系的数据

D.无序数据元素

2-10
若一棵二叉树的后序遍历序列是{ 1, 3, 2, 6, 5, 7, 4 }，中序遍历序列是{ 1, 2, 3, 4, 5, 6, 7 }，则下列哪句是错的？

A.2是1和3的父结点

B.7是5的父结点

C.这是一棵完全二叉树

D.这是一棵二叉搜索树

解析：
给出了后序+中序 那么我们可以推出整棵树来。
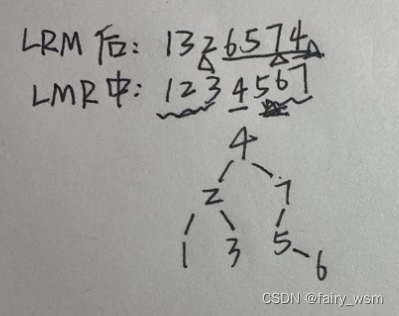所以C为错的。

判断题

1-1
存在一棵总共有2016个结点的二叉树，其中有16个结点只有一个孩子。F
解析：
1-2
将一棵完全二叉树存于数组中（根结点的下标为1）。则下标为23和24的两个结点是兄弟。F
解析：
下标从1开始，2n与2n+1是兄弟

1-3
用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。F
解析：
在邻接表中有两种节点结构，一种是顶点节点的结构，由顶点域和第一条邻接边的指针域构成；另一种是边节点结构，由邻接点域和指向下一条邻接边的指针域构成。所以用邻接表存储图所用的空间大小与图的顶点数和边数都有关。

1-4
无向连通图所有顶点的度之和为偶数。T
解析：
无向图中，一条边连接两个顶点，所以被计算两次，因此所有顶点的度之和为偶数。

1-5
在一个有权无向图中，若b到a的最短路径距离是12，且c到b之间存在一条权为2的边，则c到a的最短路径距离一定不小于10。T
解析：
如果c到a的距离小于10，那么b到a的最短路径肯定小于12
b->c->a

1-6
已知一棵二叉树的先序遍历结果是ABC,　则CAB不可能是中序遍历结果。T
解析：
先序遍历为根左右，中序遍历为左根右
所以b肯定在c的左边

1-7
Prim 算法是通过每步添加一条边及其相连的顶点到一棵树，从而逐步生成最小生成树。T
解析：
Prim首先以一个节点作为最小生成树的初始节点，然后以迭代的方式找出最小生成树中各节点权重最小的边，并加到最小生成树中。（加入之后如果产生回路了就要跳过这条边，选择下一个节点）当所有节点都加入到最小生成树后，就找到了这个连通图的最小生成树。

1-8
在任一有向图中，所有顶点的入度之和等于所有顶点的出度之和T
解析：
有向图中一条边是一个节点的出度，必定是另一个节点的入度，所以所有顶点的入度之和等于所有顶点的出度之和。

1-9
如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G中一定有回路。F
解析：
比如有两个连通分量

1-10
对N（≥2）个权值均不相同的字符构造哈夫曼树，则树中任一非叶结点的权值一定不小于下一层任一结点的权值。T
解析：
权值越大编码长度越短，权值越小编码长度越长。节点所在层数越小编码长度就越短，权值就越大。