👉️ 力扣原文

前言

二叉树前序遍历的顺序为：
先遍历根节点；
随后递归地遍历左子树；
最后递归地遍历右子树。

二叉树中序遍历的顺序为：
先递归地遍历左子树；
随后遍历根节点；
最后递归地遍历右子树。

题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例

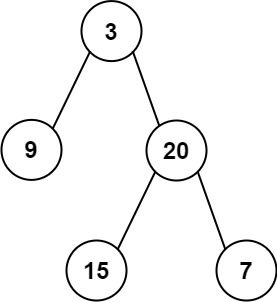
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

输入: preorder = [-1], inorder = [-1]
输出: [-1]

分析思路1

递归:
根据前序遍历中的第一个节点创建根节点，并找到该节点在中序遍历中的位置，进而确定左子树和右子树各自的前序遍历和中序遍历的范围。由此可以递归地构建左子树和右子树，并将左右子树分别挂在根节点的左右孩子上。

题解1

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || inorder == null || preorder.length != inorder.length) {
                return null;
        }
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        return buildTreeHelper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1, map);

    }

    
    private TreeNode buildTreeHelper(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd, Map<Integer, Integer> map) {
        if (preStart > preEnd || inStart > inEnd) {
            return null;
        }
        int rootVal = preorder[preStart];
        TreeNode root = new TreeNode(rootVal);
        int rootIndex = map.get(rootVal);
        int leftSize = rootIndex - inStart;
        root.left = buildTreeHelper(preorder, preStart + 1, preStart + leftSize, inorder, inStart, rootIndex - 1, map);
        root.right = buildTreeHelper(preorder, preStart + leftSize + 1, preEnd, inorder, rootIndex + 1, inEnd, map);
        return root;
    }
}

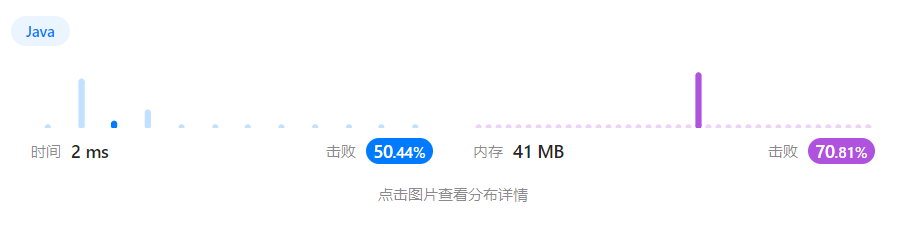
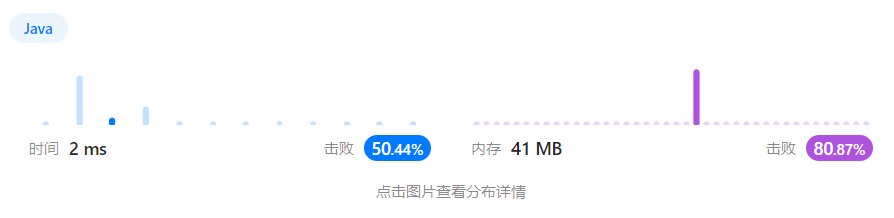
执行结果

分析思路2

迭代:

1. 初始化一个栈和根节点，将根节点入栈。
2. 遍历前序遍历数组，对于每一个值，创建一个新节点，并将其作为当前节点的左儿子，然后将新节点入栈。
3. 如果当前值等于中序遍历数组的第一个值，则说明当前节点的左子树已经构造完成，将栈顶元素出栈，即当前节点变为其父节点，然后将新节点作为当前节点的右儿子，并将新节点入栈。
4. 重复步骤 3，直到前序遍历数组遍历完毕。

题解2

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || inorder == null || preorder.length == 0 || inorder.length == 0) {
        return null;
    }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode root = new TreeNode(preorder[0]);
        stack.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.length; i++) {
            TreeNode node = stack.peek();
            if (node.val != inorder[inorderIndex]) {
                node.left = new TreeNode(preorder[i]);
                stack.push(node.left);
            } else {
                while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                    node = stack.pop();
                    inorderIndex++;
                }
                node.right = new TreeNode(preorder[i]);
                stack.push(node.right);
            }
        }
        return root;
    }
}

执行结果