这是新的系列教程，在本教程中，我们将介绍使用 FPGA 实现深度学习的技术，深度学习是近年来人工智能领域的热门话题。

在本教程中，旨在加深对深度学习和 FPGA 的理解。

用 C/C++ 编写深度学习推理代码
高级综合 (HLS) 将 C/C++ 代码转换为硬件描述语言
FPGA 运行验证

在本文中，我们将循环并行化应用于先前任务并行化的推理内核，并平衡层与层之间的执行时间。

此外，当前内核的外部内存访问效率低下，因此内存访问也是瓶颈。在这种状态下，即使进行循环并行化，内存访问最终也会成为瓶颈。

当前内核瓶颈

下面转载上一篇文章中附上的内核执行时间报告。

运行时报告：

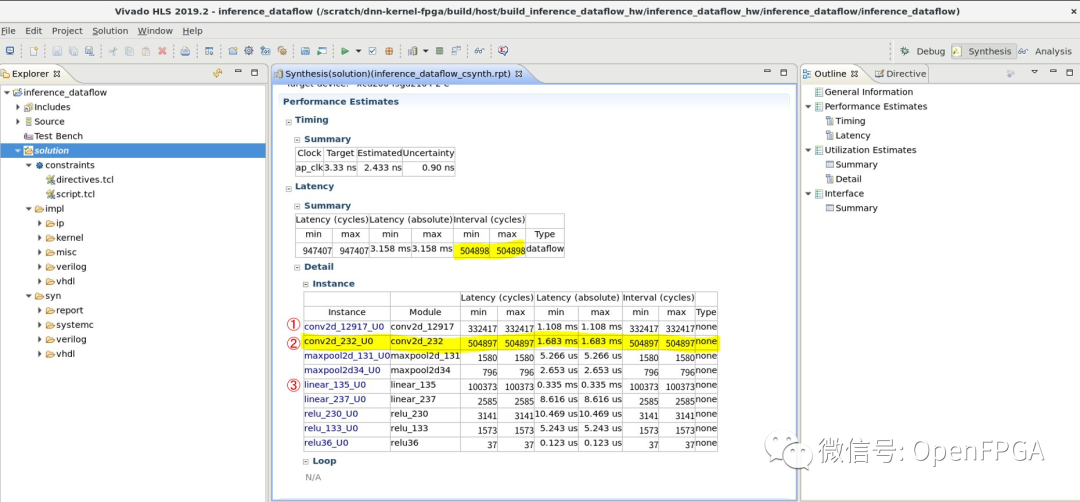
实际时间：

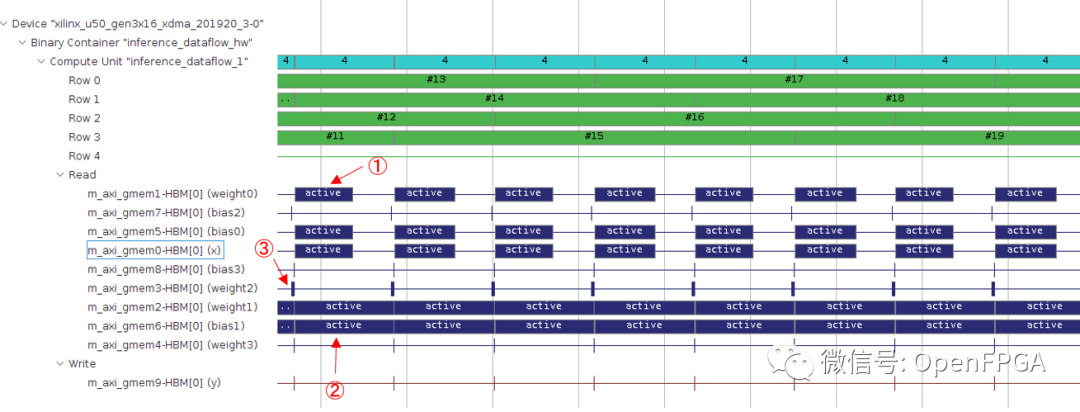
这里，每幅图中的①、②、③分别对应第一个卷积层（conv1）、第二个卷积层（conv2）和第一个全连接层（fc1）。执行时间报告显示conv2、conv1、fc1的执行时间比例为5:3:1。另一方面，在真机实践上，conv2:conv1的比例约为5:3，但fc1层的执行时间与它们相比非常短。整个推理过程的执行时间也是 12.65 ms/image，明显长于报告的吞吐量（504098 cycles / 300MHz = 1.68 ms/image）。

HLS 报告 <-> 实际机器的性能存在这种差异的原因是，HLS 报告是在假设可以在请求外部存储器的时间立即提供数据的情况下创建的。由于在真机上访问外部内存不是那么快，所以在真机上性能明显更差。

内存访问优化

我们发现内存访问效率低下，将对其进行优化。当前内核为卷积层中的每个乘法累加运算从外部 DRAM 获取系数数据。使用此配置，对 DRAM 的访问以非常细的粒度进行操作，因此 DRAM 上的负载变得非常高。

Xilinx的FPGA内部的内存层次结构如下图所示，FPGA中存在分布式RAM（Distributed RAM）、BRAM（Block RAM）、URAM（Ultra RAM）三种。

❝
https://forums.xilinx.com/t5/Xcell-Daily-Blog-Archived/UltraRAM-a-new-tool-in-the-memory-hierarchy-you-ll-want-because/ba-p/708532
❞

这些 FPGA 内部的存储器可以比 DRAM 运行得更快，并且每个周期都可以稳定地读写数据。因此，这次我们将图像、权值大小等数据提前全部复制到FPGA中，并进行修改，让每一层都从FPGA的内存中读取数据。在这种情况下，图像和权重大小读取时间足够小，因此我将坚持使用 HLS 默认值（BRAM 或分布式 RAM）。

要创建的电路框图如下所示。

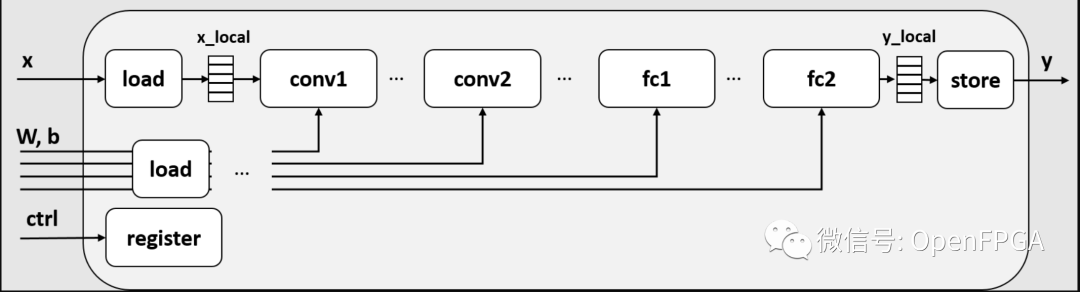
添加一个新电路x，x_local临时存储来自本地内存的 DRAM 输入的数据。至于loadweight输出，它也是将层的数据缓冲到本地内存中，并从端口biasfc2y_localy输出结果。

在此图中，为简单起见，假定本地缓冲区是单个缓冲区。对于上次解释的任务并行化，这个缓冲区应该是乒乓缓冲区。

要在 HLS 中实现此电路，代码中定义load一个store函数和一个本地storememcpy缓冲区。其实我们不需要自己定义这个函数，如果我们使用C标准库，load它会自动生成一个高效的电路，所以我们就用它。

代码如下所示：

111 void inference_with_local_buffer(const float x[kMaxSize],
112                                  const float weight0[kMaxSize], const float bias0[kMaxSize],
113                                  const float weight1[kMaxSize], const float bias1[kMaxSize],
114                                  const float weight2[kMaxSize], const float bias2[kMaxSize],
115                                  const float weight3[kMaxSize], const float bias3[kMaxSize],
116                                  float y[kMaxSize]) {
117 #pragma HLS dataflow
118 #pragma HLS interface m_axi port=x offset=slave bundle=gmem0
...
151
152   const std::size_t x_size = 1 * 28 * 28;
153   const std::size_t w0_size = 4 * 1 * 3 * 3, b0_size = 4;
...
157   const std::size_t y_size = 10;
158
159   float x_local[x_size];
160   float w0_local[w0_size], b0_local[b0_size];
...
164   float y_local[y_size];
165
166   // fetch to local buffer
167   std::memcpy(x_local, x, x_size * sizeof(float));
168   std::memcpy(w0_local, weight0, w0_size * sizeof(float));
...
176
177   // run inference with local buffer
178   dnnk::inference(x_local,
179                   w0_local, b0_local,
180                   w1_local, b1_local,
181                   w2_local, b2_local,
182                   w3_local, b3_local,
183                   y_local);
184
185   // store to global buffer
186   std::memcpy(y, y_local, y_size * sizeof(float));
187 }

第167行，将DRAM上的内存复制到xFPGAx_local内部的内存中。之后，我们用来运行x_local推理dnnk::inferencey_localmemcpy函数，最终输出到DRAM。

以下是综合此电路并在真机上执行的日志。可以看出，原本需要 12.65 [ms/image] 的执行时间已经减少到 1.61 [ms/image]。

$ ./host/run_inference ./host/inference_with_local_buffer_hw.xclbin inference_with_local_buffer 1
Elapsed time: 1.61029 [ms/image]
accuracy: 0.973

卷积层在这个内核中的表现也稍好一些，因为原始内核在卷积层内部没有 DRAM 访问，将处理周期总数减少到 504898 -> 481378 个周期。481378个周期在300MHz转换时为1.604 ms，与上述真机执行时间（1.61 ms）相差无几。因此，从inference_with_local_buffer可以看出，对于使用本地缓冲区进行缓存的函数，内存访问时间不会对整体性能产生不利影响。

通过循环并行化加速卷积层

到此为止，HLS报告的执行时间和真机差不多，所以本文的主题循环并行化将从以下开始。

在卷积函数的最内层循环中，大致进行了以下三个过程。

像素，负载权重
像素，权重的乘积
将乘法结果添加到求和寄存器

这三个过程都是在下面的卷积函数的第31行完成的。

17         for (int32_t ich = 0; ich < in_channels; ++ich) {
 18           for (int32_t kh = 0; kh < ksize; ++kh) {
 19             for (int32_t kw = 0; kw < ksize; ++kw) {
...
 31               sum += x[pix_idx] * weight[weight_idx];
 32             }
 33           }
 34         }

粗略地说，上述内核的处理流程如下图所示。

这里，假设处理load需要1个周期，fmul处理需要3个周期，fadd处理需要4个周期。第一行是迭代（循环的迭代次数）i，下一行是下一次迭代i+1，最后i+2是处理后的波形。在不提取循环并行度的情况下，每次迭代的处理完全不重叠，每次迭代需要8个周期的处理时间。

比如load2-9、10-17等周期，电路都没有运行，一直运行可以进一步提高性能。load电路一直运行时的波形如下图所示。

到目前为止，下一次迭代每 8 个周期开始一次，但在本例中，下一次迭代每 1 个周期开始一次。以这种方式提取不同迭代之间的并行性称为循环并行化。可以进行一次迭代的时间间隔称为II（Iteration Interval），本例中写为II=1。

在循环并行中，并行的抽象方式与之前的任务并行几乎相同。然而，任务并行性提取帧之间的并行性，而循环并行性提取每一层内处理迭代之间的并行性。此外，为了提取任务并行性，需要同时处理多个帧，因此存在需要将多个帧的输入数据预先扩展到FPGA上的DRAM等限制。另一方面，由于循环并行仅在帧内完成，因此可以没有特别限制地提取并行。

循环并行化的方法很简单，#pragma HLS pipeline II=1只需要在循环中添加符号，如下所示：这样做kw可以优化变量的循环，以便它们可以一次处理一个循环。

17         for (int32_t ich = 0; ich < in_channels; ++ich) {
 18           for (int32_t kh = 0; kh < ksize; ++kh) {
 19             for (int32_t kw = 0; kw < ksize; ++kw) {
...
 30 #pragma HLS pipeline II=1
 31               sum += x[pix_idx] * weight[weight_idx];
 32             }
 33           }
 34         }

仅通过添加#pragma HLS pipeline II=1就可以实现II=1，但即使对上述修改后的内核进行综合，也会输出以下记录：目标（Target）为II=1，但实际电路（Final）为II=4。

INFO: [v++ 204-61] Pipelining loop 'Loop 1.1'.
INFO: [v++ 204-61] Pipelining result : Target II = 1, Final II = 4, Depth = 12.

这是因为在第31行的处理中，下一次迭代的计算依赖于上一次迭代sum += ...的相加结果。另一方面，x[pix_idx]的加载处理和x[pix_idx]*weight[weight_idx]的乘法处理不依赖于前迭代的结果，因此可以先处理。

#pragma HLS pipeline应用后的波形大致如下。

load, fmul可以先运行，fadd但要等到上一次迭代完成后才能运行，所以整体faddII受到 4 个周期延迟的速率限制。

通过复制和寄存器提高性能

前面说了这个卷积不可能每个循环都做，因为i+1迭代的结果取决于迭代次数。i在这里，sum通过将 sum 寄存器复制成四个，我们改变了依赖关系，使得i迭代依赖于迭代的结果i-4。由于用文字难以理解，目标波形如下所示。

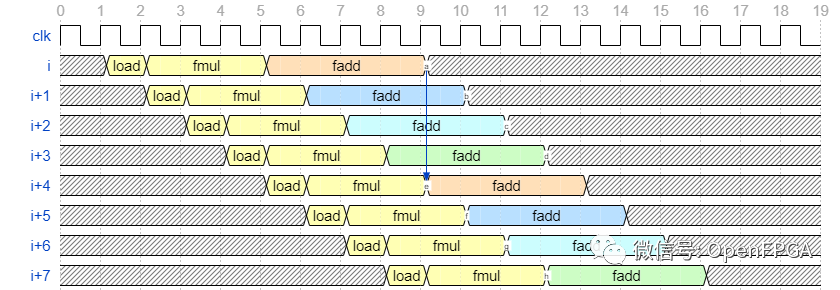
fadd(橙色、蓝色、水色和绿色)的颜色fadd代表输出目标寄存器，输出目标寄存器在每个循环中切换。这样，从第5周期开始到第8周期结束的一次迭代i的计算结果将被fadd第9周期的迭代首次使用。

要创建的电路应该是上面描述的那种，但是从 Vivado HLS/Vitis 创建它需要稍微特殊的编写方式。以下描述基于名为 shift_register_c 的 SDAccel 教程的内容。

下面是使用移位寄存器的卷积函数的代码。

82 static void conv2d_pipelined_v2(const float* x, const float* weight, const float* bias, int32_t width, int32_t height,
 83                                 int32_t in_channels, int32_t out_channels, int32_t ksize, float* y) {
 84   static const int kShiftRegLength = 4;
 85
 86   for (int32_t och = 0; och < out_channels; ++och) {
 87     for (int32_t h = 0; h < height; ++h) {
 88       for (int32_t w = 0; w < width; ++w) {
 89         float shift_reg[kShiftRegLength + 1];
 90 #pragma HLS array_partition variable=shift_reg complete
 91
 92         int32_t glob_idx = 0;
 93         for (int32_t ich = 0; ich < in_channels; ++ich) {
 94           for (int32_t kh = 0; kh < ksize; ++kh) {
 95             for (int32_t kw = 0; kw < ksize; ++kw) {
 96 #pragma HLS pipeline II=1
...
109               float mul = x[pix_idx] * weight[weight_idx];
110
111               // local sum
112               for (int i = 0; i < kShiftRegLength; ++i) {
113                 if (i == 0) {
114                   if (glob_idx < kShiftRegLength) {
                        // 外部でゼロ初期化するとシフトレジスタに推論されなくなるため、ループ内でゼロ初期化相当の処理
115                     shift_reg[kShiftRegLength] = mul;  
116                   } else {
                        // 初期化時以外
117                     shift_reg[kShiftRegLength] = shift_reg[0] + mul;
118                   }
119                 }
120
121                 shift_reg[i] = shift_reg[i + 1];
122               }
123
124               ++glob_idx;
125             }
126           }
127         }
128
129         // global sum
130         float sum = 0.f;
131         for (int i = 0; i < kShiftRegLength; ++i) {
132 #pragma HLS pipeline II=1
133           sum += shift_reg[i];
134         }
135
136         // add bias
137         sum += bias[och];
138
139         y[(och * height + h) * width + w] = sum;
140       }
141     }
142   }
143 }

主要有以下三个区别：

1、移位寄存器定义（L89-L90）
2、本地求和：重复求和寄存器（L111-L122）的求和
3、全局求和：重复求和寄存器（L130-L134）之间的求和处理

1的移位寄存器定义将4+1求和寄存器定义为FPGA上的寄存器。+1只是一个临时寄存器，按照C语言语法只用来临时存放加法的结果，在高级综合时删除。第90 行添加了一个新的 pragma（#pragma HLS array_partition）（）以将移位寄存器定义为寄存器（完整），默认情况下将其推断为 BRAM。pragma 本身可以做很多其他事情，但我将在下一个数据并行化中触及细节。

2 的本地求和在四个求和寄存器上累加乘法结果 (mul)。这里，glob_idx是ich、kh、kw 3个循环的索引。通常情况下，shift_reg[glob_idx % 4] += mul可以复制我们这次正在做的输出寄存器，但是这样，高级综合结果II=4就不会改变。因此，这里使用官方示例中也使用的移位处理（shift_reg[i] = shift_reg[i + 1]）II=1来实现这一点。每次对这两个寄存器进行shift_reg[0]加法mul运算shift_reg[0]时，它所包含的求和寄存器的数字（0 到 3）每个周期都会发生变化。

3 的全局求和对四个求和寄存器执行求和运算。#pragma HLS pipeline我们也在这里指定，但fadd由于延迟，这里我们没有 II=1。

此修改允许kw循环的 II 为 1，从而实现最有效的循环并行化。另一方面，此修复程序并没有提供 4 倍的加速，因为它添加了另一个全局求和循环。

评估

检查综合结果

比较以下三种配置的性能。

内存访问优化后（无循环并行）
#pragma HLS pipeline II=1
使用移位寄存器加速后

结果总结在下表中。

方法	卷积层 II	第二层卷积迭代（二）	整个推理过程的迭代区间（二）
无循环并行	8	481377	481378
pipeline	4	257153	257154
移位寄存器后	1	127009	172482

着眼于第2个卷积层，通过pipeline改变loop parallelism -> onlypipeline获得了约1.87倍的性能提升，通过应用shift register -> 获得了约2.02倍的性能提升。这里，本来是II = 4 -> II = 1，所以我们希望性能提升4倍左右，但实际上，上面描述的全局求和过程占用了很多时间，所以速度未获得提升。

下面是应用移位寄存器后配置的 HLS 报告。

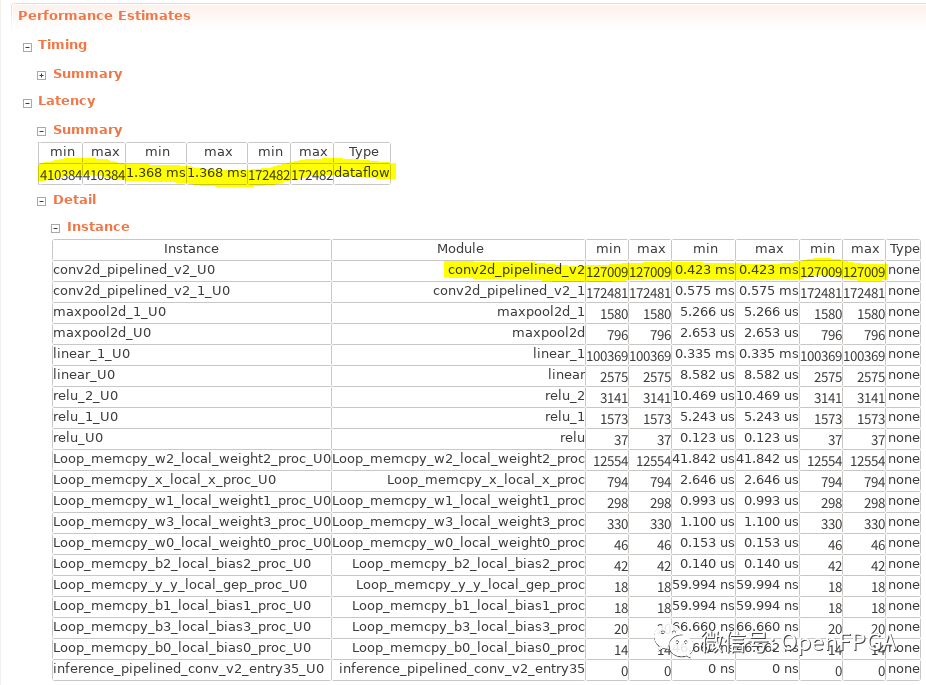
在前面的推理过程中，瓶颈是第二个卷积层（conv2d_pipelined_v2），但这里的瓶颈是第一个卷积层（conv2d_pipelined_v2_1）。这是因为第一个卷积层是 1ch，3×3 卷积，所以一开始每个像素只执行九次操作。在这种情况下，由于能够执行 II=1 的局部求和而带来的性能增益被添加全局求和循环所带来的性能损失所抵消，反之性能下降。另一方面，随着输入通道数和内核大小的增加，局部求和处理的性能提升变得更加明显，因此这种优化在大规模网络中变得更加有效。

总结

到目前为止通过调整的加速率如下。

方法	执行时间（毫秒/图像）	比以前的实施提速	相对于基线的改进百分比
基线	20.81	1.00	1.00
任务并行化	12.65	1.65	1.65
通过本地缓冲区减少外部存储器访问	1.61	7.86	12.93
循环并行化（仅限卷积层）	0.61	2.64	34.11