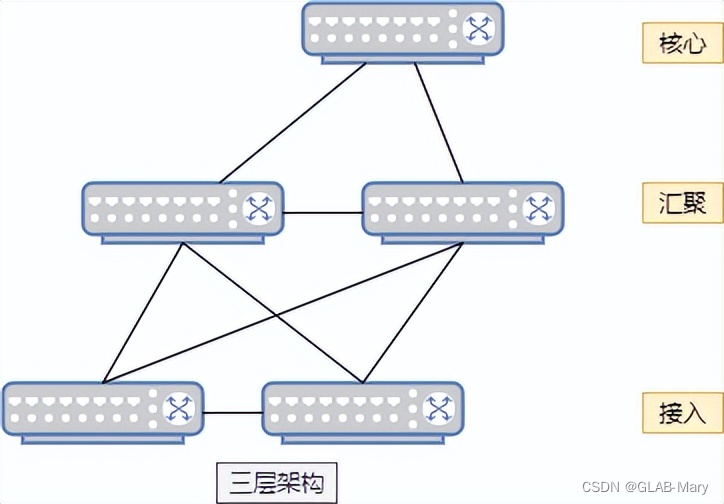
非比较排序之计数排序
- 之前讲的七种排序方法的话,都是比较排序;除此之外还有三种非比胶排序:计数排序,基数排序,桶排序。后面两个实际应用没啥,没啥价值。非比较排序的话,他的条件都比较苛刻,就是说他一般不适用于常规的场景,适用于特殊的场景。
- 计数排序其实就是基于哈希,只不过就是现在还没学过而已,计数排序就是说不借助于这么去比较大小。
- 计数排序的话就是说去统计每个数据出现的次数。比如说你已经知道这个数组总的数据范围是在0~9,然后他就是先给每一个数据建立一个坑位0.1.2.3.4.5.6.7.8.9(其实就是可以新创建一个数组,然后注意:这个新数组的下标就对应到数据数值),这些专属的坑位就是用来统计这个数据它出现的次数,最先开始初始化新数组为0。
- 然后就是去遍历原先的数组,然后就会得到一个又一个的原先数组当中的数值,然后再把这些得到的数值对应到新数组的下标,对新数组下标所指向的那个数据(最开始初始化为0)进行++。
- 然后接下来就可以进行排序,对数组直接怼上去覆盖。首先遍历这个计数新数组,比如说对那个新数组从左到右进行遍历的话,1出现了2次,那么就在原数组给他从头开始覆盖两个2;然后3出现了1次,再在原数组接着继续去覆盖一个3…
从绝对映射优化到相对映射
- 当前方式还不够好,比如说现在我需要排序的数据是100,105,105,101,102,100,109,100。那我如果采用绝对映射的话,我要开110个元素的数组,然后开了那么大结果映射出来就只单单映射在最尾巴那部分,浪费空间啊,前面空间白开了啊。因此采用绝对映射的话是不妥的
- 相对映射:首先必须得去找到原数组当中的最大值与最小值,然后把两者的差range给他算出来。
- 然后我新开计数数组的时候,我开一个range+1大的就OK了。此时不是绝对映射,映射关系如下:
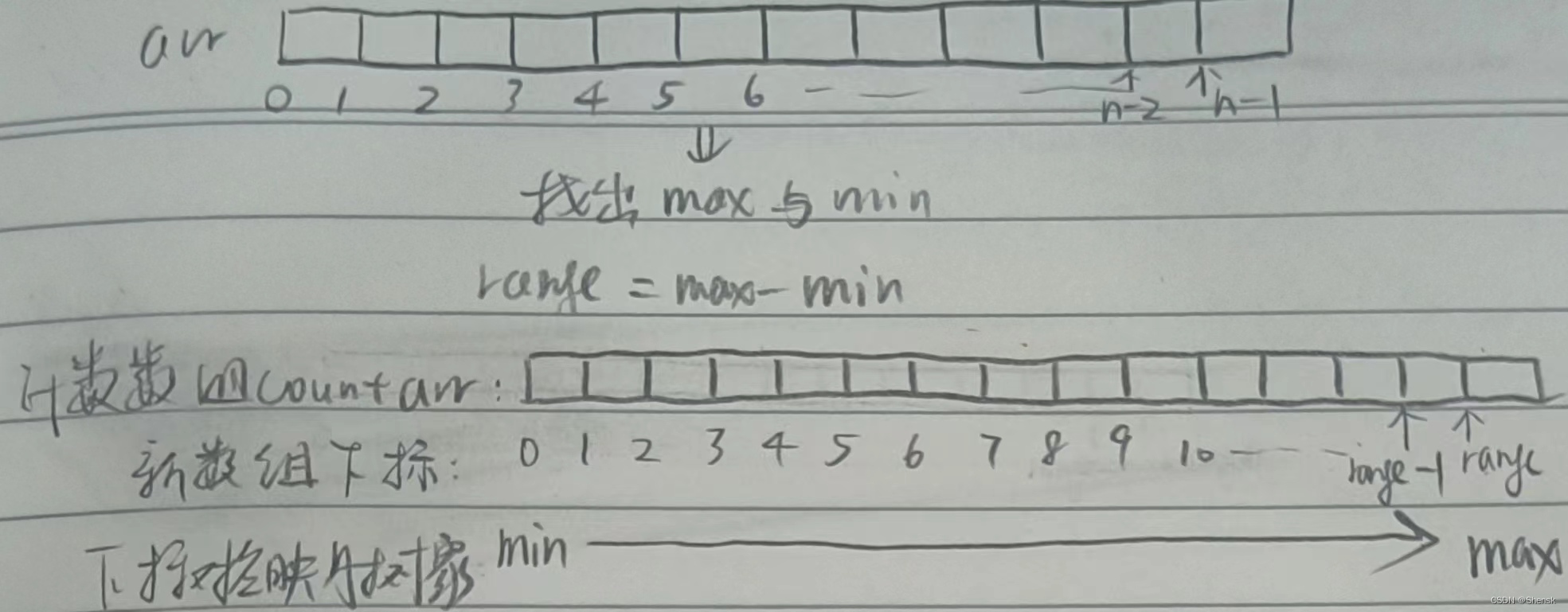
- 总而言之,计数新数组下标与原先数组数值之间是属于映射关系: 新数组下标 + min = 原先数组数值
- 如果说是在绝对映射的情况之下,那有负数是肯定不可以的,但如果是像上面那样进行相对映射的话,是OK了的。
void CountSort(int* arr, int n)
{
int min = arr[0];
int max = arr[0];
for (int i = 0; i < n; i++)
{
if (arr[i] < min)
{
min = arr[i];
}
if (arr[i] > max)
{
max = arr[i];
}
}
int range = max - min;
int* countarr = (int*)malloc(sizeof(int) * (range + 1));
if (countarr == NULL)
{
perror("malloc failed");
return;
}
memset(countarr, 0, sizeof(int) * (range + 1));
for (int i = 0; i < n; i++)
{
countarr[arr[i] - min]++;
}
int j = 0;
for (int i = 0; i <= range; i++)
{
while (countarr[i]--)
{
arr[j++] = i + min;
}
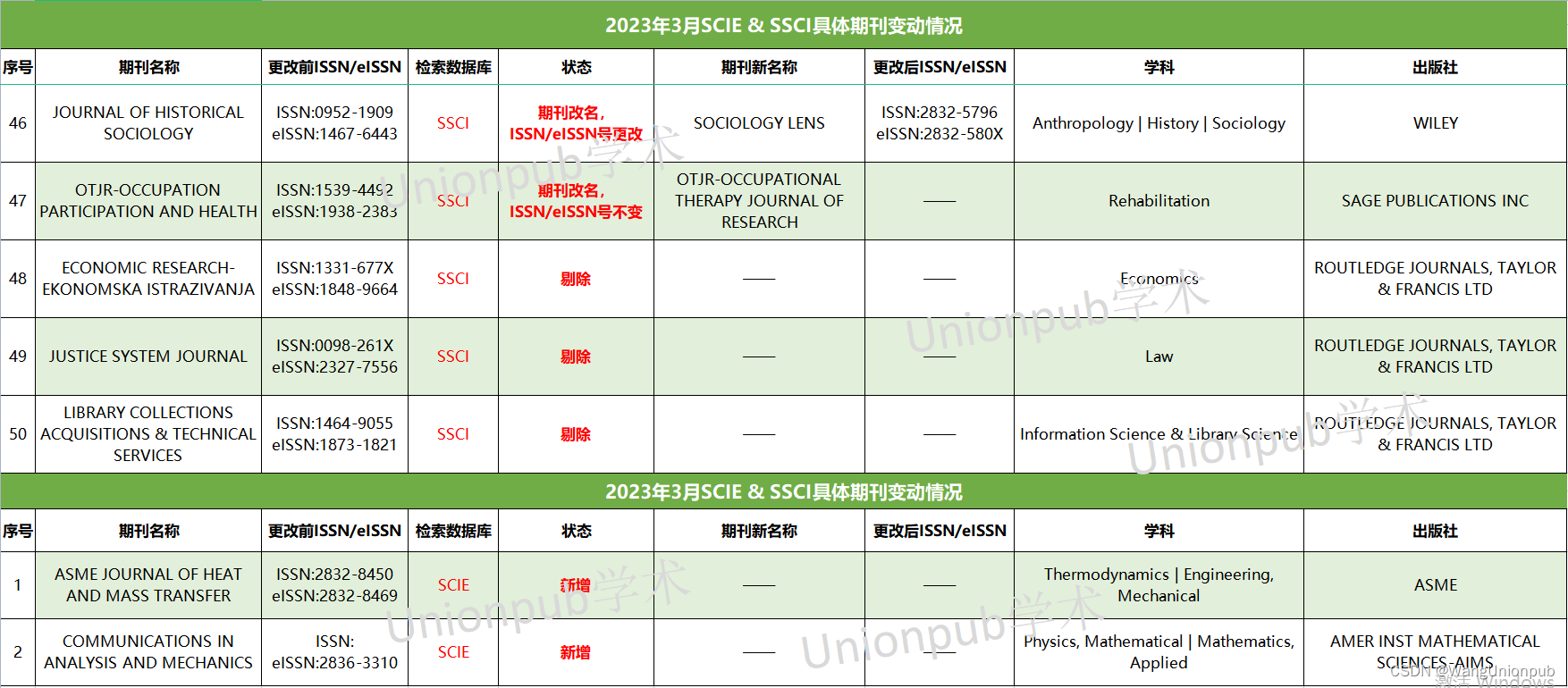
}
free(countarr);
}
- 但这种方法有时候也不太行的,当碰到另外一种场景,相对映射他就又挂了。当你数字范围分散的时候又裂开了。
- 因此计数排序适合范围集中且范围不大的整形数组排序。不适合非整形(如浮点,字符串,因为这时候你无法对应映射到新的计数数组的下标去了,只有整型可以)与范围分散的场景。
时间复杂度
- 首先在这种排序的话,它对原数组首先得遍历一遍去找到最大值,最小值,这就是O(N)。
- 然后还得再去遍历一遍这个原先的数组,对于数组当中的每一个数值通过映射关系找到他在新数组当中对应的下标,然后把这个下标对应位置的新数组数值给他加1。这也是O(N)
- 然后还得去遍历一遍新数组,与此同时,从开头开始要对原先数组进行覆盖操作。当新数组遍历完成之后,此时原先数组已经焕然一新,变成排序完成好之后了。这个过程需要O(range+1),这个range就是max-min.
- 所以总共的时间复杂度就是O(N和range的较大值)

6.