线性回归和逻辑斯蒂回归的区别

线性回归一般用于预测连续值变量，如房价预测问题。
线性回归的一般表达式为：
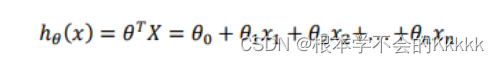
在这里插入图片描述
代价函数为MSE（均方误差）：

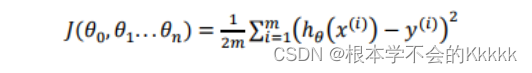
其中权重theta的更新，一般可选用梯度下降等相关优化方法。由于MSE对特征值的范围比较敏感，一般情况下对会对特征进行归一化处理。

逻辑回归虽然叫做回归，但是其主要解决分类问题。可用于二分类，也可以用于多分类问题。由于线性回归其预测值为连续变量，其预测值在整个实数域中。而对于预测变量y为离散值时候，可以用逻辑回归算法（Logistic Regression）逻辑回归的本质是将线性回归进行一个变换，该模型的输出变量范围始终在 0 和 1 之间。
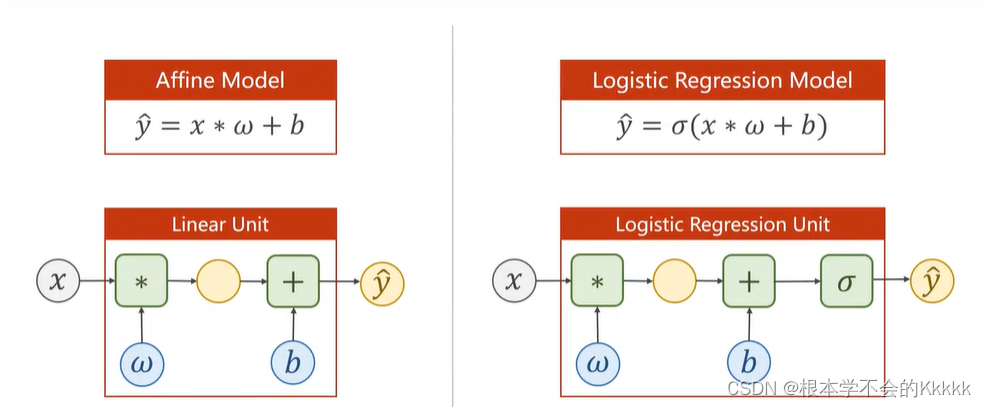
在这里插入图片描述

本质上，逻辑回归就是线性回归再进行了sigmod变换，其值变化到(0,1).

课上代码

from torch.nn import ModuleList
import torch
import torch.nn.functional as F

# 准备数据
x_data = torch.Tensor ([[1.0], [2.0], [3.0]])
y_data = torch.Tensor ([[0], [0], [1]])

# 定义网络
class LogisticRegressionModel (torch.nn.Module):
  def __init__(self):
    super(LogisticRegressionModel, self).__init__()
    self.linear = torch.nn.Linear (1, 1)
  
  def forward (self, x):
    y_pred = F.sigmoid (self.linear(x))
    return y_pred

model = LogisticRegressionModel ()
# 定义优化器和损失函数
criterion = torch.nn.BCELoss (size_average = False)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

for epoch in range (1000):
  y_pred = model (x_data)
  loss = criterion (y_pred, y_data)
  print (epoch, loss.item())

  optimizer.zero_grad()
  loss.backward ()
  optimizer.step()

print ('w=', model.linear.weight.item())
print ('b=', model.linear.bias.item())

x_test = torch.Tensor ([[4.0]])
y_test = model (x_test)
print ('y_pred = ', y_test.data)