目录
见见猪跑(初步了解位图)
位图的模拟实现
位图的应用
1、给定100亿个整数,设计算法找到只出现一次的整数
2、给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
3、位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
哈希切分
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址? 与上题条件相同,如何找到top K的IP?
布隆过滤器
应用场景
布隆过滤器的删除
实现代码
见见猪跑(初步了解位图)
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断这个数是否在这40亿个数中。【腾讯】
关键字:无符号整数。既然是一个整数,那么40亿个,存储就是一个麻烦的事。
根据我们所学:

只存储就需要16G,显然是不合理的,因此我们使用位图来很好的解决了这个问题。
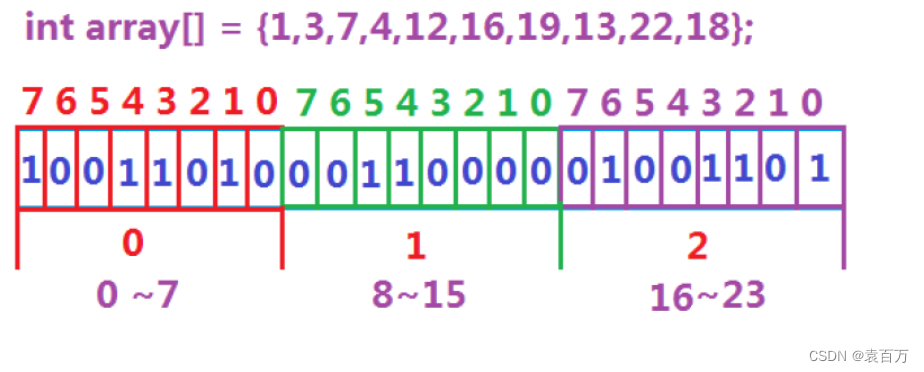
我们已知最小的存储单位是比特,一个比特位可以表示1或0两种状态。我们使1代表存在,0代表不存在。这样的话40亿数据只需要40亿个比特位,一共只需要0.5G,非常好用。
并且将我们需要处理的数据一一映射进每一个比特位上面。
每一个8比特位的空间我们以一个两个字节的char来开辟。
位图的模拟实现
class bitset
{
public:
//构造函数赋初值
bitset()
{
//_bits.resize((N >> 3) + 1, 0);
//开辟大小,并初始化为0
_bits.resize(N / 8 + 1, 0);
}
//插入
void set(size_t x)
{
//i在_bits去找在第几个char里面
size_t i = x / 8;
//j在char中去找在第几个位(bit)里面
size_t j = x % 8;
//将对应位置1
_bits[i] |= (1 << j);
}
//删除
void reset(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
//将所在位置0
_bits[i] &= (~(1 << j));
}
//检查
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
//若在该位有值(为1)则返回的就是非0的
return _bits[i] & (1 << j);
}
private:
vector<char> _bits;
};
void test_bit_set()
{
//bitset<100> bs1;
//
//开辟了42亿的空间
//
bitset<-1> bs2;
//bitset<0xffffffff> bs2;
bs2.set(100);
cout << bs2.test(10) << endl;
cout << bs2.test(100) << endl;
bs2.set(9999);
cout << bs2.test(9999) << endl;
}位图的应用
1、给定100亿个整数,设计算法找到只出现一次的整数
解析:
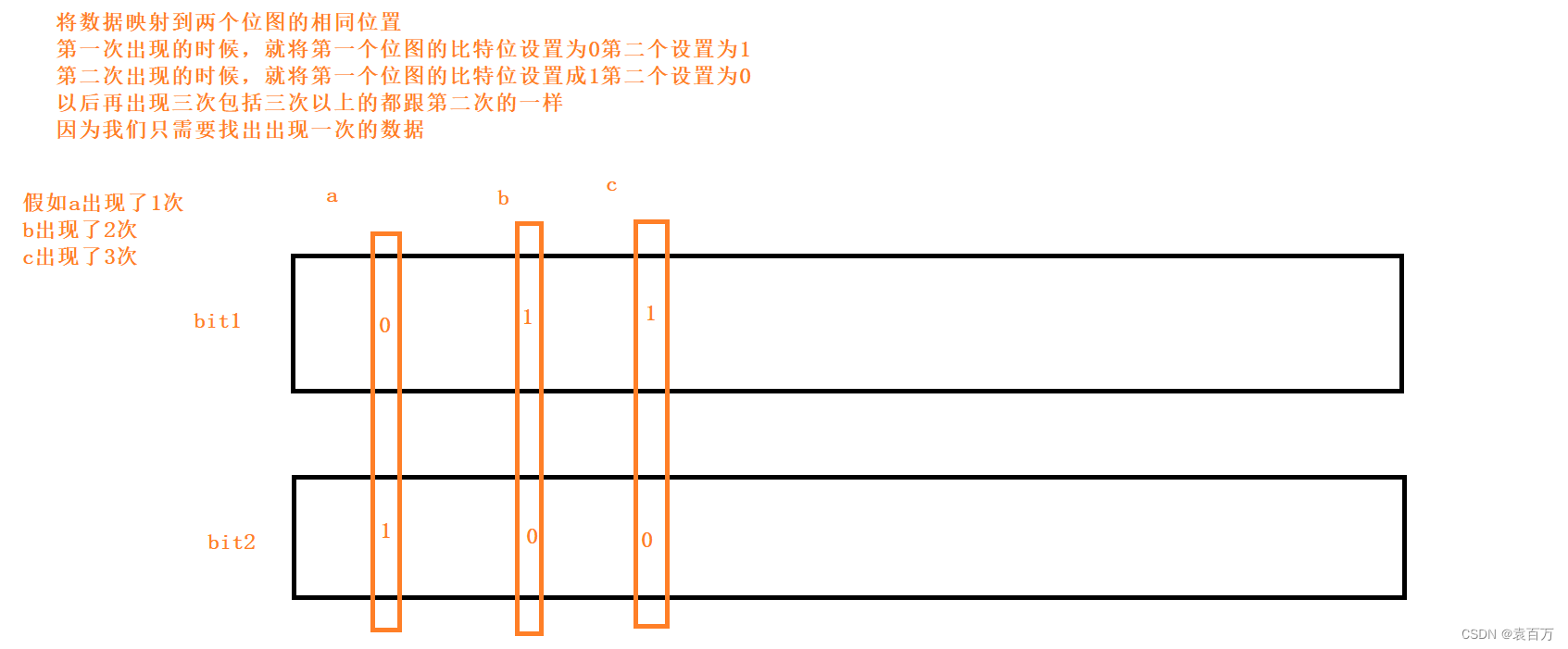
“100亿整数”当我们看到这种字眼,首先直接将这些数据存储到整型里面是不现实的,因此要用到位图。然后我们看到需要找出只出现一次的整数,我们之前的位图只能表示一种状态,就是再或者不在,那么如何才能表示多种状态呢,我们想到了再使用一个位图。
#pragma once
//
//注意:
//无论给定多少个数据我们无符号整型范围最大也就到4294967295--2^32
namespace mwb
{
template<size_t N>
class bitset
{
public:
//构造函数赋初值
bitset()
{
//_bits.resize((N >> 3) + 1, 0);
//开辟大小,并初始化为0
_bits.resize(N / 8 + 1, 0);
}
//插入
void set(size_t x)
{
//i在_bits去找在第几个char里面
size_t i = x / 8;
//j在char中去找在第几个位(bit)里面
size_t j = x % 8;
//将对应位置1
_bits[i] |= (1 << j);
}
//删除
void reset(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
//将所在位置0
_bits[i] &= (~(1 << j));
}
//检查
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
//若在该位有值(为1)则返回的就是非0的
return _bits[i] & (1 << j);
}
private:
vector<char> _bits;
};
template<size_t N>
class twobitset
{
public:
twobitset() {}
void set(size_t x)
{
//插入前的状态
if (!_bs1.test(x) && !_bs2.test(x))//00
{
_bs2.set(x);//01
}
else if (!_bs1.test(x) && _bs2.test(x))//01
{
_bs1.set(x);//1
_bs2.reset(x);//0 // 10
}
// 如果本来就是 10 那么后边再插入都是10
}
void PrintOnce()
{
for (size_t i = 0; i < N; i++)
{
if (!_bs1.test(i) && _bs2.test(i))
{
cout << "只出现一次的数:" << i << endl;
}
}
cout << endl;
}
public:
bitset<N> _bs1;
bitset<N> _bs2;
};
void test_twobitset()
{
twobitset<100> tbs;
int a[] = { 3,5,6,7,8,9,33,55,67,3,3,3,5,9,33 };
//首先把每个数都set进去
for (auto e : a)
{
tbs.set(e);
}
tbs.PrintOnce();
}
}
2、给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
和第一问类似,开两个位图,分别将两组数据映射进位图,两个位图对应的比特位均为1即为交集。
3、位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
同第一问,开两个位图,00代表不存在,01代表出现一次,10代表出现两次,11代表出现两次以上。
哈希切分
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址? 与上题条件相同,如何找到top K的IP?
通过哈希映射的方式可以将相同的IP放进同一个哈希桶里面,然后再使用map。
注意:很可能相同的比较多(数据量大),会导致map不能用。这样我们需要递归再次哈希映射。
布隆过滤器
布隆过滤器(Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。它是用多个哈希函数,将一个数据映射到位图结构中,可以用来告诉你 “某样东西一定不存在或者可能存在”。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
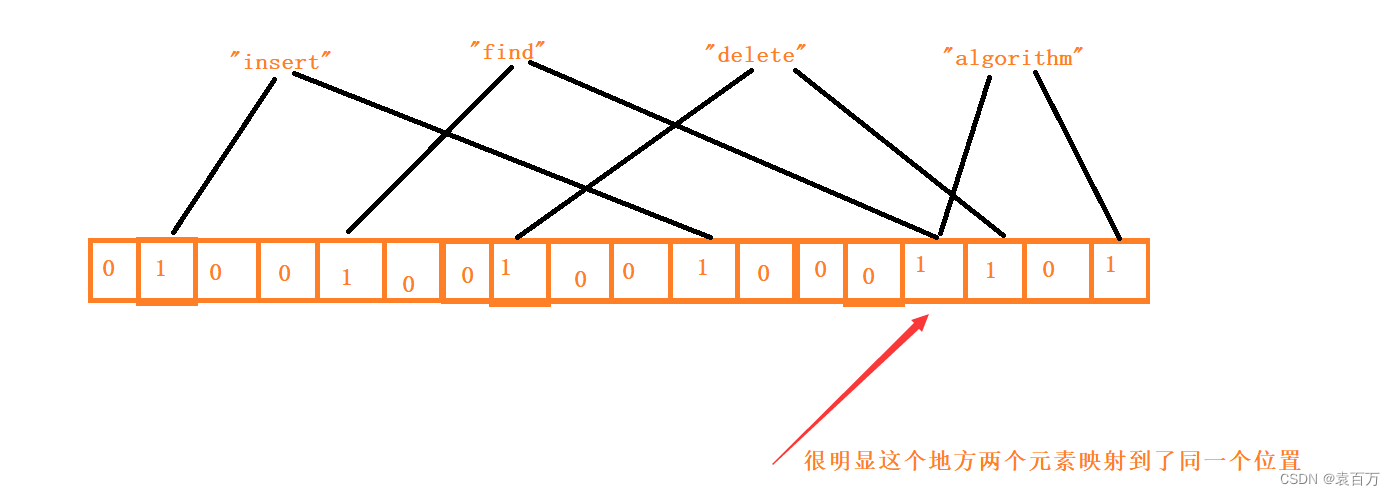
通过图中有一处两个元素映射到了同一个位置,我们也可以发现一点。当我们判断一个元素是否在时是不准确的,但是我们要去判断是否不在是准确的。
那么通过如何做法可以提高我们的准确率呢?这跟我们点外卖需要看好拼多的店的做法是一样的,我们就把这个值去映射多个位置(使用不同的哈希映射函数)然后判断这个值在不在的时候分别检查这几个位置,通过多个映射位置来确定这个值是否存在。
注意:可惜的是我们只能降低误判率,但不能完全消除误判。
应用场景
比如我们在玩游戏的时候需要注册的ID,我们就可以利用布隆过滤器首先对你输入的ID名字进行过滤。(因为布隆过滤器具有优秀的判重能力)。这样就可以在这些数据进入数据库之前进行一个很好的过滤,也减轻了在数据库中比对的负担。增加了效率。
布隆过滤器的删除
我们在布隆过滤器中删除的时候需要注意的是,当一个比特位同时被两个数据映射的时候就要小心了。如果我们因为需要删除其中的某一个数据,将这个比特位给置0了那么另一个数据必将收到影响。因此如果我们真的需要删除数据,在我们在布隆过滤器映射数据的时候哦就要搞一个计数器,来对在这一位上一共映射了多少个数据进行计数,如果需要删除直接计数器-1即可。
实现代码
#pragma once
#include<bitset>
namespace mwb
{
struct BKDRHash
{
size_t operator()(const string& key)
{
size_t hash = 0;
for (auto ch : key)
{
hash *= 131;
hash += ch;
}
return hash;
}
};
struct APHash
{
size_t operator()(const string& key)
{
unsigned int hash = 0;
int i = 0;
for (auto ch : key)
{
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ (ch) ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ (ch) ^ (hash >> 5)));
}
++i;
}
return hash;
}
};
struct DJBHash
{
size_t operator()(const string& key)
{
unsigned int hash = 5381;
for (auto ch : key)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
struct JSHash
{
size_t operator()(const string& s)
{
size_t hash = 1315423911;
for (auto ch : s)
{
hash ^= ((hash << 5) + ch + (hash >> 2));
}
return hash;
}
};
template<size_t N,
size_t X = 6,
class K = string,
class HashFunc1 = BKDRHash,
class HashFunc2 = APHash,
class HashFunc3 = DJBHash,
class HashFunc4 = JSHash>
class BloomFilter
{
public:
void set(const K& key)
{
size_t hash1 = HashFunc1()(key) % (X * N);
size_t hash2 = HashFunc2()(key) % (X * N);
size_t hash3 = HashFunc3()(key) % (X * N);
size_t hash4 = HashFunc4()(key) % (X * N);
_bs.set(hash1);
_bs.set(hash2);
_bs.set(hash3);
_bs.set(hash4);
}
bool test(const K& key)
{
size_t hash1 = HashFunc1()(key) % (X * N);
if (!_bs.test(hash1))
{
return false;
}
size_t hash2 = HashFunc1()(key) % (X * N);
if (!_bs.test(hash2))
{
return false;
}
size_t hash3 = HashFunc1()(key) % (X * N);
if (!_bs.test(hash3))
{
return false;
}
size_t hash4 = HashFunc1()(key) % (X * N);
if (!_bs.test(hash4))
{
return false;
}
//前面判断都是准确,不存在误判
//可能存在误判,映射几个位置都冲突,就会误判
return true;
}
private:
std::bitset<N * X> _bs;
};
void test_bloomfilter1()
{
string str[] = { "猪八戒", "孙悟空", "沙悟净", "唐三藏", "白龙马1","1白龙马","白1龙马","白11龙马","1白龙马1" };
BloomFilter<10> bf;
for (auto& str : str)
{
bf.set(str);
}
for (auto& s : str)
{
cout << bf.test(s) << endl;
}
cout << endl;
srand(time(0));
for (const auto& s : str)
{
cout << bf.test(s + to_string(rand())) << endl;
}
}
}