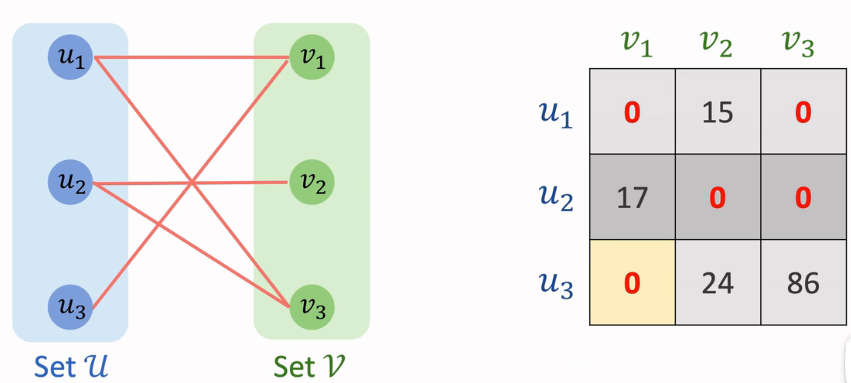
匈牙利算法主要用来解决两个问题：求二分图的最大匹配数和最小点覆盖数。
匈牙利算法事实上有两个算法，分别解决指派问题和二分图最大匹配求解问题，此处算法指求解指派问题的匈牙利算法。

处理流程

方法一

具体如何实现呢？

代码实现

行列归约

主要执行的便是这个函数，在该函数中执行行规约，列规约操作，同时使用cover_zeros.calculate()来进行试指派，得出独立0元素所在的行与列

def calculate(self):
    """
    实施匈牙利算法的函数
    """
    result_matrix = self._cost_matrix.copy()

    # 步骤 1: 矩阵每一行减去本行的最小值
    for index, row in enumerate(result_matrix):
        result_matrix[index] -= row.min()

    # 步骤 2: 矩阵每一列减去本行的最小值
    for index, column in enumerate(result_matrix.T):
        result_matrix[:, index] -= column.min()
    # print('步骤2结果 ',result_matrix)
    # 步骤 3： 使用最少数量的划线覆盖矩阵中所有的0元素
    # 如果划线总数不等于矩阵的维度需要进行矩阵调整并重复循环此步骤
    total_covered = 0
    while total_covered < self._size:
        time.sleep(1)
        # print("---------------------------------------")
        # print('total_covered: ',total_covered)
        # print('result_matrix:',result_matrix)
        # 使用最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量
        cover_zeros = CoverZeros(result_matrix)
        single_zero_pos_list = cover_zeros.calculate()
        covered_rows = cover_zeros.get_covered_rows()
        covered_columns = cover_zeros.get_covered_columns()
        total_covered = len(covered_rows) + len(covered_columns)

        # 如果划线总数不等于矩阵的维度需要进行矩阵调整（需要使用未覆盖处的最小元素）
        if total_covered < self._size:
            result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns)
    # 元组形式结果对存放到列表
    self._results = single_zero_pos_list
    # 计算总期望结果
    value = 0
    for row, column in single_zero_pos_list:
        value += self._input_matrix[row, column]
    self._totalPotential = value

打勾划线与试指派

完成试指派操作，主要是为了完成打勾划线操作。其实际上完成的是原理中的步骤2操作，不过，其在代码实现上是按照下面的流程实现的。

方法二（与方法一完全相同）

其实执行上面的步骤与文章最开始的步骤2效果完全是一致的。如下图：

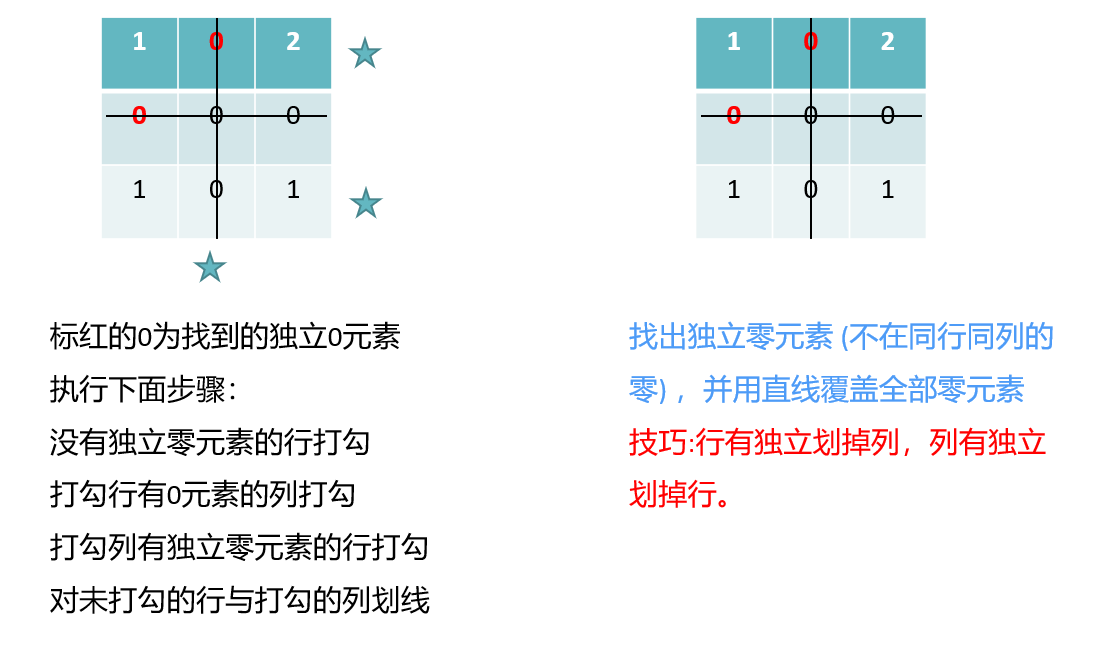
同时关于为何要进行未划线的减去最小值，则是为了增加0元素的数量，而交叉线的加上最小值其实也是做的初等列变换，让其不出现负值。
事实上步骤三按照第二种方式：未划线的行减去最小值，划线的列加上最小值来理解就更直观了。

def calculate(self):
    '''进行计算'''
    # 储存勾选的行和列
    ticked_row = []
    ticked_col = []
    marked_zeros = []
    # 1、试指派并标记独立零元素
    while True:
        # print('_zero_locations_copy',self._zero_locations_copy)
        # 循环直到所有零元素被处理（_zero_locations中没有true）
        if True not in self._zero_locations_copy:
            break
        self.row_scan(marked_zeros)

    # 2、无被标记0（独立零元素）的行打勾
    independent_zero_row_list = [pos[0] for pos in marked_zeros]
    ticked_row = list(set(range(self._shape[0])) - set(independent_zero_row_list))#的到未标记行
    # 重复3,4直到不能再打勾
    TICK_FLAG = True
    while TICK_FLAG:
        # print('ticked_row:',ticked_row,'   ticked_col:',ticked_col)
        TICK_FLAG = False
        # 3、对打勾的行中所含0元素的列打勾
        for row in ticked_row:
            # 找到此行
            row_array = self._zero_locations[row, :]
            # 找到此行中0元素的索引位置
            for i in range(len(row_array)):
                if row_array[i] == True and i not in ticked_col:
                    ticked_col.append(i)
                    TICK_FLAG = True

        # 4、对打勾的列中所含独立0元素的行打勾
        for row, col in marked_zeros:
            if col in ticked_col and row not in ticked_row:
                ticked_row.append(row)
                FLAG = True
    # 对打勾的列和没有打勾的行画画线
    self._covered_rows = list(set(range(self._shape[0])) - set(ticked_row))
    self._covered_columns = ticked_col

    return marked_zeros

在该方法内部有个row_scan方法，该方法是对行进行逐行扫描，选出独立零元素，marked_zeros即为选定的0元素。

 def row_scan(self, marked_zeros):
        '''扫描矩阵每一行，找到含0元素最少的行，对任意0元素标记（独立零元素），划去标记0元素（独立零元素）所在行和列存在的0元素'''
        min_row_zero_nums = [9999999, -1]
        for index, row in enumerate(self._zero_locations_copy):  # index为行号 找出改行最少的0元素
            row_zero_nums = collections.Counter(row)[True]
            if row_zero_nums < min_row_zero_nums[0] and row_zero_nums != 0:
                # 找最少0元素的行
                min_row_zero_nums = [row_zero_nums, index]#记录0的个数，哪行。
        # 最少0元素的行  min_row_zero_nums  记录0的个数，哪行
        row_min = self._zero_locations_copy[min_row_zero_nums[1], :]
        # 找到此行中任意一个0元素的索引位置即可
        row_indices, = np.where(row_min)#如两个0元素，分别为0，2，则返回前面的0即可。
        # 标记该0元素
        # print('row_min',row_min)
        marked_zeros.append((min_row_zero_nums[1], row_indices[0]))
        # 划去该0元素所在行和列存在的0元素
        # 因为被覆盖，所以把二值矩阵_zero_locations中相应的行列全部置为false，先将列变为false，再将行变为false
        self._zero_locations_copy[:, row_indices[0]] = np.array([False for _ in range(self._shape[0])])
        self._zero_locations_copy[min_row_zero_nums[1], :] = np.array([False for _ in range(self._shape[0])])

矩阵调整

最后便是试指派失败后的矩阵调整了

def _adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):
    """计算未被覆盖元素中的最小值（m）,未被覆盖元素减去最小值m,行列划线交叉处加上最小值m"""
    adjusted_matrix = result_matrix
    # 计算未被覆盖元素中的最小值（m）
    elements = []
    for row_index, row in enumerate(result_matrix):
        if row_index not in covered_rows:
            for index, element in enumerate(row):
                if index not in covered_columns:
                    elements.append(element)
    min_uncovered_num = min(elements)
    # print('min_uncovered_num:',min_uncovered_num)
    # 未被覆盖元素减去最小值m
    for row_index, row in enumerate(result_matrix):
        if row_index not in covered_rows:
            for index, element in enumerate(row):
                if index not in covered_columns:
                    adjusted_matrix[row_index, index] -= min_uncovered_num
    # print('未被覆盖元素减去最小值m',adjusted_matrix)

    # 行列划线交叉处加上最小值m
    for row_ in covered_rows:
        for col_ in covered_columns:
            # print((row_,col_))
            adjusted_matrix[row_, col_] += min_uncovered_num
    # print('行列划线交叉处加上最小值m',adjusted_matrix)
    return adjusted_matrix

最大匹配边

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i)
{
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]) //有边且未访问
        {
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int Hungarian()
{
    int cnt = 0;
    for (int i = 1; i <= M; ++i)
    {
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}

补充

事实上，上面的指派问题实际上是求最小权重二分图匹配问题

经过转换：是不是很眼熟，这不就是二分图匹配问题吗，这里就转换成了最大匹配，同时这里的最大匹配也是完全匹配。