前言

上一篇文章我们复习了一下运放的基本知识，尽量的用简单的描述带大家去理解运算放大器：

带你理解运算放大器

对于运放的使用，存在着一些经典常用的应用电路，这个其实网络上已经有大量的文章做记录总结了，作为电子工程师必备的知识，我自己也觉得有必要用一篇文章来做个记录总结。

本文的电路分析都是基于上面推荐博文来进行的，如果有朋友不懂为什么还望先查看上面的博文《带你理解运算放大器》。

我是矜辰所致，全网同名，尽量用心写好每一系列文章，不浮夸，不将就，认真对待学知识的我们，矜辰所致，金石为开！

一、电压跟随器

电压跟随器，电路图如下：

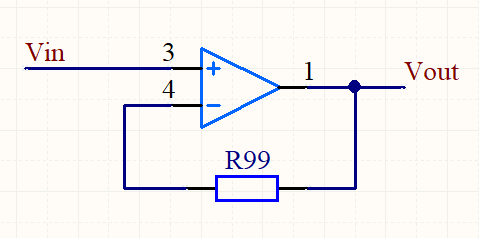
电路分析：

（本文所有的运放电路分析， V+ 表示运放同向输入端的电压，V- 表示反向输入端的电压 。）

Vout = V- ≈ V+ = Vin
➩ Vout ≈ Vin

1.1 电压跟随器反馈电阻需不需要？

在上面的电压跟随器示例中，我画上了一个反馈电阻 R99，大家在学习的运放的时候，可能很多地方也会提一下这个反馈电阻，很多地方会说可加可不加，效果一样。

电阻需不需要加：

但是本文这里个人建议使用电压跟随的的时候反馈电阻要加上！

至于原因，简单来说就是可以防止干扰，让电路更稳定。

电阻需要加多大：

几百欧姆 到 10K 之内。

二、反向比例电路

2.1 反向比例基本电路

最简单的反向比例运放电路，如下图：

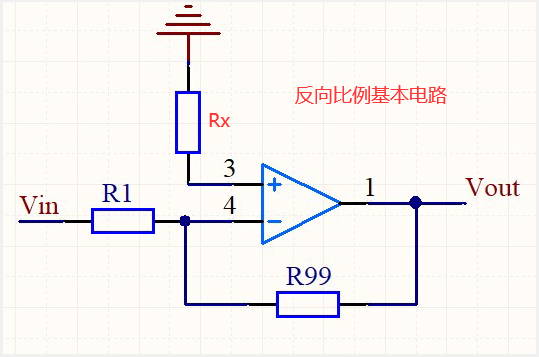
分析：

V+ 接 GND
➩ V- ≈ V+ = 0
R1 和 R99 上电流一样：
➩ ( Vin - V- ) / R1 = ( V- - Vout ) / R99
➩ Vin / R1 = - Vout / R99
➩ Vout = - (R99 / R1)* Vin

运放的对称性说明

在上图中有一个 Rx 称之为直流平衡电阻， 实际设计的时候电阻大小应满足公式：

Rx = R1 // R99

简单来说为了使内部的差分放大器尽量处于平衡状态，提高电路的共模抑制比和减小零漂。

所以在本文后面电路的介绍时候，都会按照这个原则。

2.2 T型反馈网络

其实 T 型反馈和上面反向比例基本电路一样，只不过多加了一个简单电路分析的工作而已，这个以前在笔记本上，那也记录一下把。

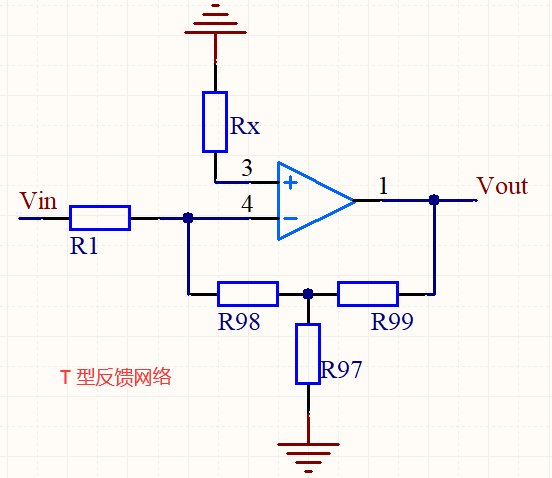
分析：

这个电路有必要把电流流向标注一下，如下图：

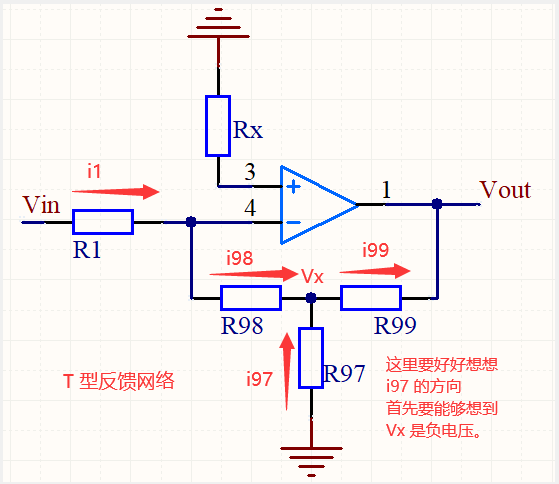
V+ 接 GND
➩ V- ≈ V+ = 0
R1 和 R98 上电流一样： i1 = i98
➩ ( Vin - V- ) / R1 = ( V- - Vx ) / R98
➩ Vin / R1 = - Vx / R98
➩ Vx = - (R98 / R1) Vin
R99 上的电流 = R98 上的电流 + R97 上的电流
➩ i99 = i98 + i97
➩（Vx - Vout）/ R99 = (V- - Vx) / R98 + (0 - Vx) / R97
其中 V- = 0， 再把 Vx 代入公式
➩ Vx/R99 - Vout/R99 = -Vx/R98 - Vx/R97
➩- R98 * Vin / R1 * R99 - Vout / R99 = R98 * Vin / R1 * R98 + R98 * Vin / R1 * R97
➩- Vout / R99 = Vin / R1 + R98* Vin / R1 * R97 + R98 * Vin / R1 * R99
➩- Vout / Vin = R99 / R1 + R98 * R99 / R1 * R97 + R98 / R1
➩ Vout = - Vin * ( R99 / R1 + R98 * R99 / R1 * R97 + R98 / R1)

算死我了 = =！后面的电路不这么算了，直接给出最终结果把，因为很多都是经典的电路，自己不需要过多的算，大家应用起来也能找到最终的公式。

上面的分析我只是用了一种计算方式，这里推荐一篇博文，关于 T 型反馈网络的计算方法：

运算放大器的应用之：T形电阻网络公式的三种推导方法

T 型反馈网络的用途：

为了避免一味的增加反馈电阻而导致的干扰，使用 T 型网络可以在不增加反馈电阻的情况下保证放大倍数，其实就是增加放大倍数的另外一种办法，增加反馈电流。

三、同向比例电路

同向比例检录也是比较简单的常用的基本电路之一，电路如下：

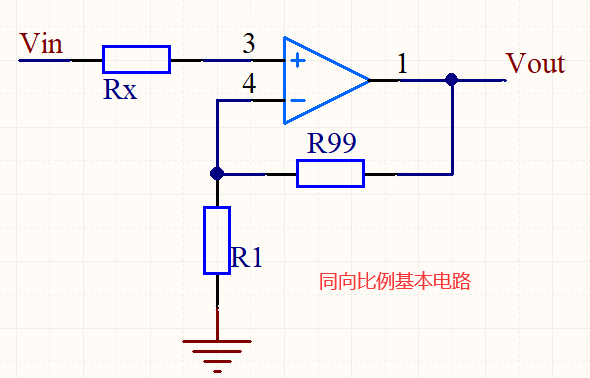
分析：

V+ = Vin
R1 和 R99 电流相等：
➩ (Vout - V-) / R99 =( V- - 0) / R1
➩ Vout = R99 * V- / R1 + V-
➩ Vout = [1 + (R99 / R1)]Vin
.
Rx = R1 // R99

3.1 同向比例与反向比例的对比

既然同向比例运算电路也值么好算，而且还不用取反，那么为什么还需要反向比例运放电路呢？

这就不得不说一下他们各自的特点：

同向比例电路的优点：

• 输入阻抗高，对输入信号的干扰很小，信号源内阻的影响基本上可以忽略不计，典型应用作为电压跟随器使用

缺点：

• 容易产生自激振荡，输入端有一定的共模电压，这个共模电压是我们不想要的，使用时候需要运放具有较高的共模抑制比。

反向比例电路的优点：

• 输入电压为零，因为运放输入的共模电压越小越好，反向比例只存在差模信号，抗干扰能力强 。

缺点：

• 输入阻抗小，那么信号源的内阻就不能忽略。
• 当需要较大的放大倍数时，在反馈电阻不变的情况下（因为反馈电阻也不是越大越好）输入电阻就要选择的更小，信号源的内阻就越不能忽略，对输出的影响就越大。

四、加减运算电路

上面几个电路是运放最基础最常用的电路，接下来也是一些常用电路，但是博主自己一般来说用得都比较少，所以我们这里目前只做基础记录，后期用到的时候再来详细的分析。

4.1 反向求和电路

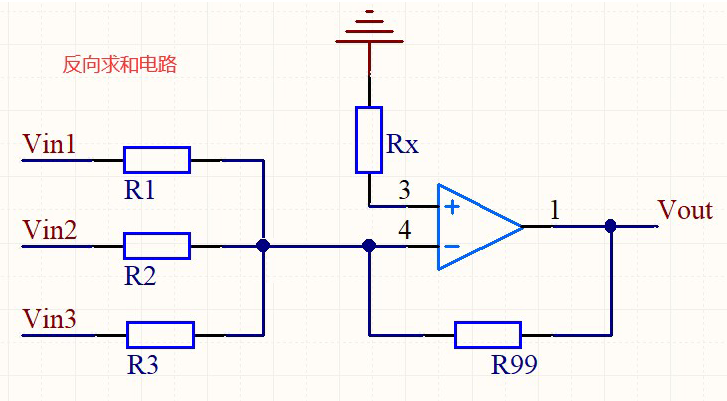
分析：

R1上的电流 + R2电流 + R3 电流 = R99 电流：
➩ (V- - Vout) / R99 =( Vin1 - V-) / R1 + ( Vin2 - V-) / R2 + ( Vin2 - V-) / R3
➩ - Vout / R99 = Vin1 / R1 + Vin2 / R2 + Vin3 / R3
➩ Vout = - R99 * (Vin1 / R1 + Vin2 / R2 + Vin3 / R3)
.
Rx = R1 // R2 // R3 // R99
.
假如 R99 = R1 = R2 = R3
➩ Vout = -（Vin1 + Vin2 +Vin3）

4.2 同向求和电路

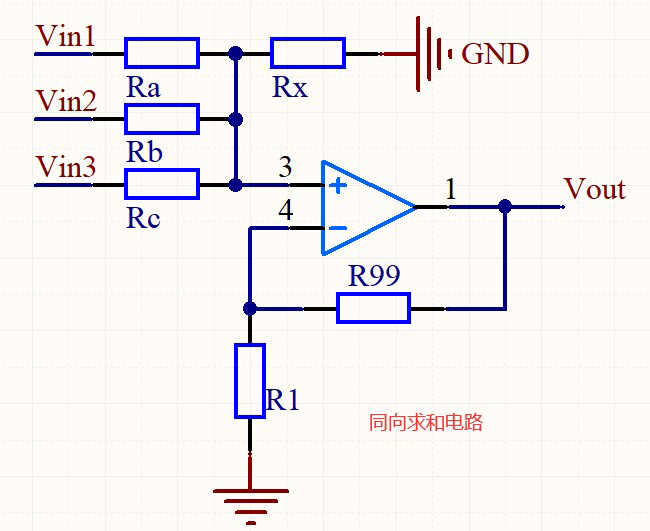
分析：

这里暂时不分析了，自己一点一点算发现好费时间也好累 = =！包括本文后续的电路也只是记录
容我展缓一下，这里记录一下
Vout = （ Ra // Rb // Rc // Rx / R1 // R99）* R99 * ( Vin1 / Ra + Vin2 / Rb + Vin3 / Rc)
.
如果 Ra // Rb // Rc // Rx = R1 // R99 ，根据我们上面的运放对称性说明，一般都会这么设计
所以 Vout = R99 * ( Vin1 / Ra + Vin2 / Rb + Vin3 / Rc)
再假设， R99 = Ra = Rb = Rc
➩ Vout = Vin1 + Vin2 +Vin3

4.3 加减电路

既然上面有加法，减法，下面看一个加减法在一起的电路：

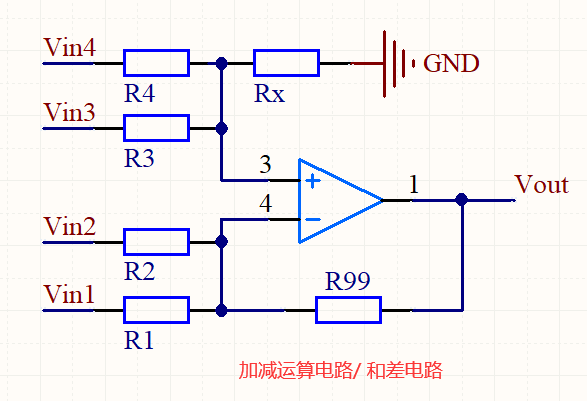
分析：

记录：
运放的对称性
➩ R1 // R2 // R99 = R3 // R4 // Rx
. 结果
Vout = R99 * （ Vin3 / R3 + Vin4 / R4 - Vin1 / R1 - Vin2 / R2）

五、积分电路

积分电路其实很有用途，以后还回来详细的补充说明，本次就先浅浅记录一下：

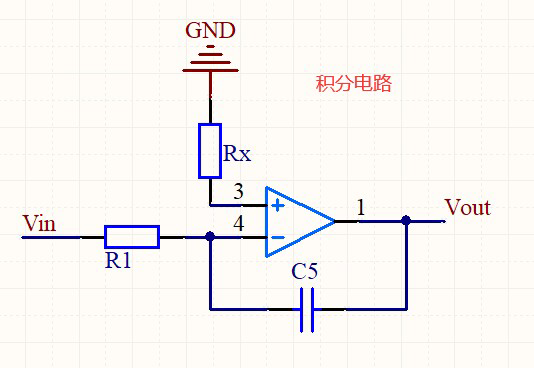
分析：

记录：
电容上的电压等于流过其电流的积分
Vout = - 1 / C ∫ i5 dt
C5 电流 和 R1 电流相等
➩ i5 = i1 = Vin / R
➩ Vout = - (1 / RC ) ∫ Vin dt
.
Vout = - (1 / RC) * Vin对时间 t 的积分

积分电路的用途：

• 将方波变成三角波
• 去除高频干扰
• 移相
• 在模数转换中，将电压量变为时间量

在使用积分电路的时候，为了防止低频信号增益过高，常在电容上并联一个电阻。

六、微分电路

微分电路就是把积分电路的 RC 调换位置：

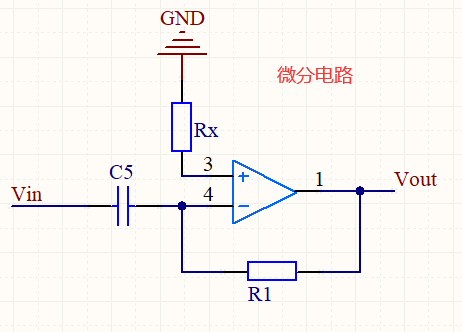
分析：

记录：
Vout = - R * C * d Vin / dt
.
乘积 R C 称为微分器的时间常数
负号表示输入和输出之间存在 180° 的相移

说明：

微分电路对高频噪声特别敏感

微分电路的用途：

微分电路可把矩形波转换为尖脉冲波，主要用于脉冲电路、模拟计算机和测量仪器中。

结语

本文也算是把老早笔记本上记录的一些常用运放电路给记录了一下，也加上了一些细节说明。

因为时间和精力问题，后面的一些电路主要以记录为主，也没有真正的去研究计算，前面的一些电路我真的是用笔在草稿纸上一点一点算的，累死我了 = =！

经常看我文章的小伙伴都知道，我的文章会随着自己新发现或者新认知保持着更新。

那么本文就暂时到这里把，谢谢大家！