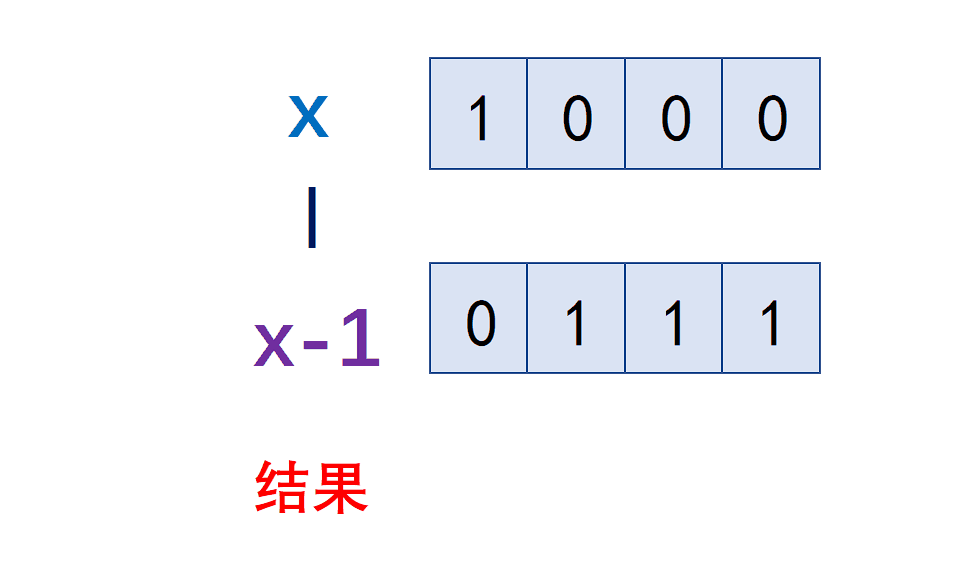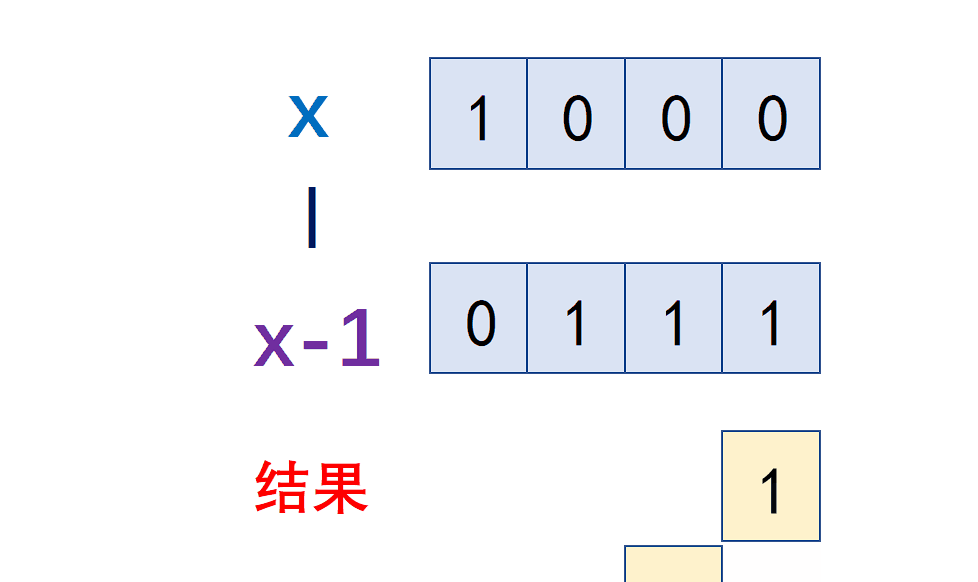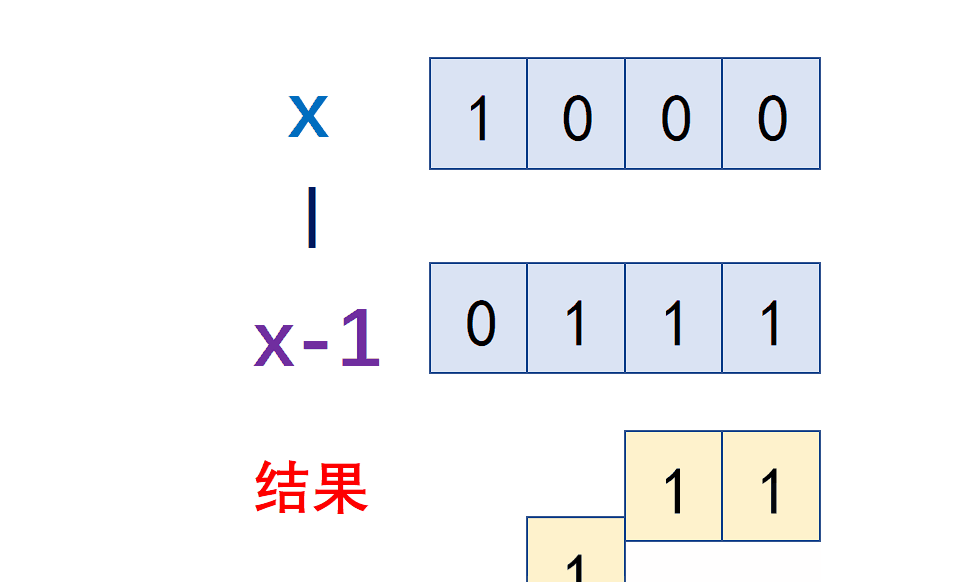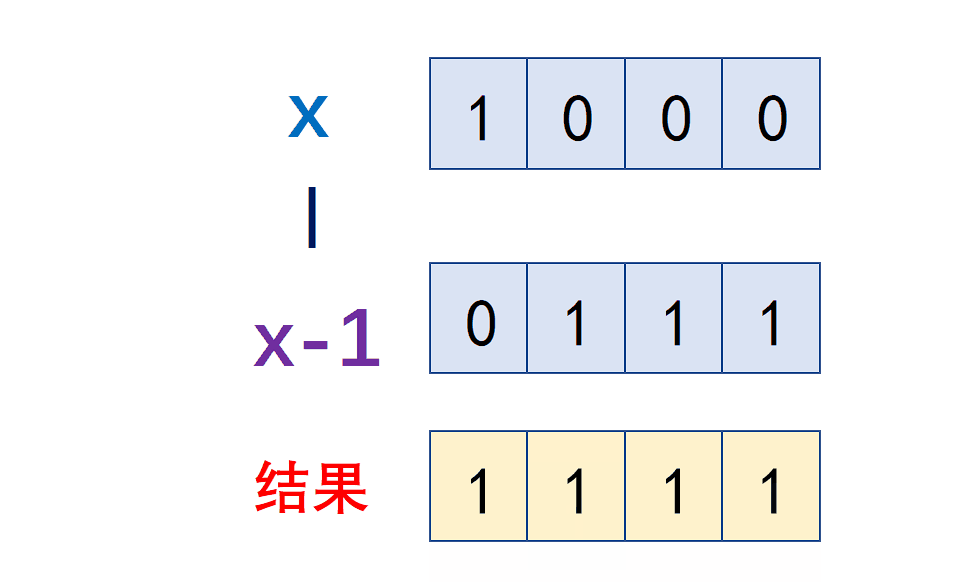
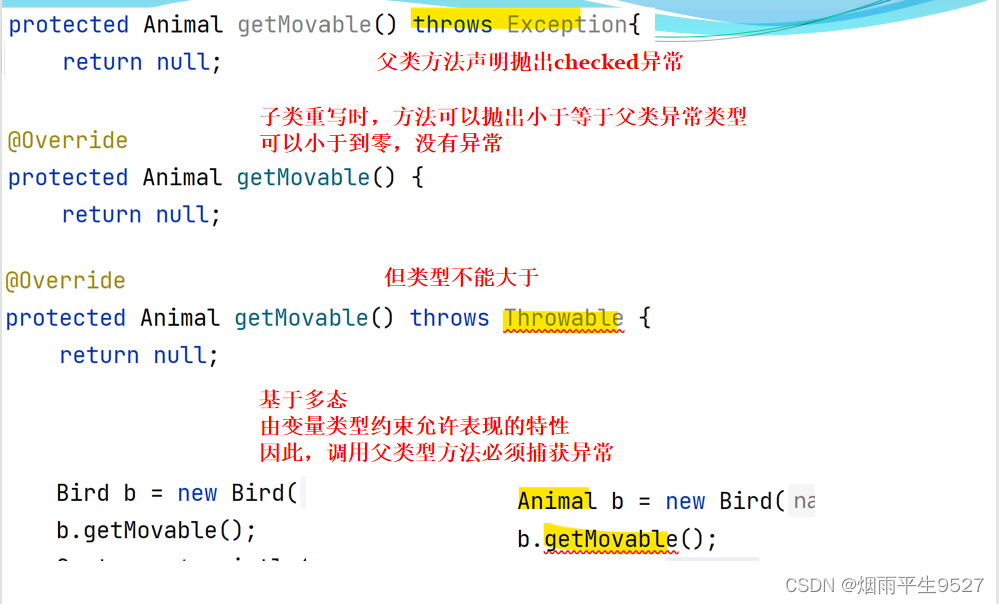
brief
横截面数据对应着某个时间点的数据。
纵向的数据对应着一系列时间点的数据,某个变量随着时间的变动被反复测量。
研究纵向数据,也许会得到“时间”的答案。

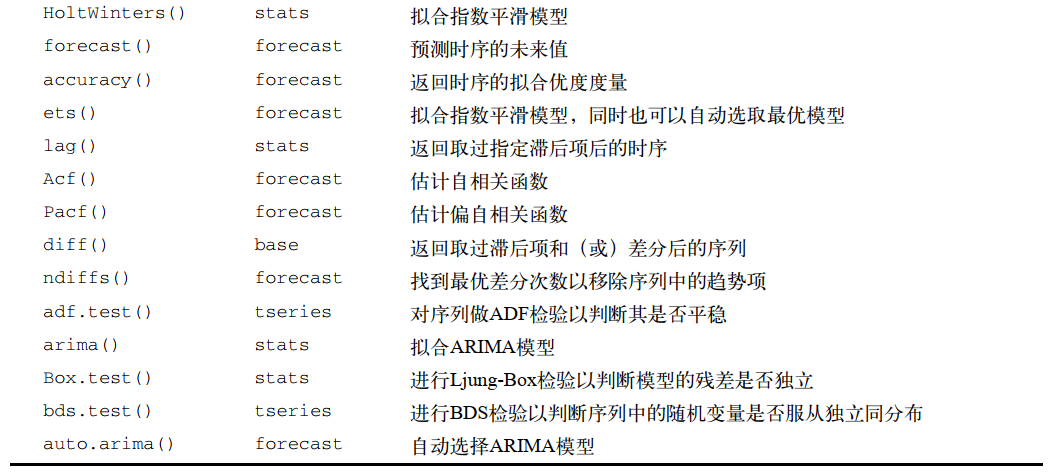
描述时间序列

生成时序对象
x <- runif(20)
ts(x)
ts(x,frequency = 12)
ts(x,frequency = 7)
y <- ts(x,start =2,frequency = 7)
plot(y)
# 时序的起止点,频率等
start(y)
end(y)
frequency(y)

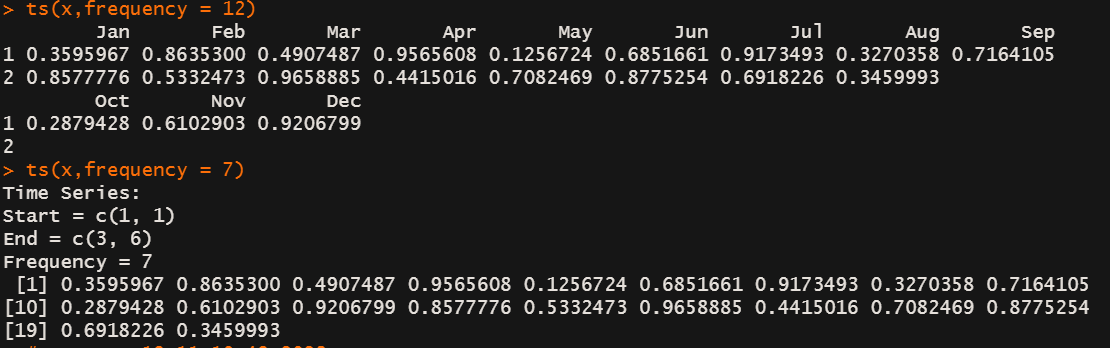

- frequence = 7 对应 daily data
- frequence = 0.2 对应每五个时间单位抽样一次
平滑时序对象

# install.packages("forecast")
library(forecast)
opar <- par(no.readonly=TRUE)
par(mfrow=c(2,2))
ylim <- c(min(Nile), max(Nile))
plot(Nile, main="Raw time series")
plot(ma(Nile, 3), main="Simple Moving Averages (k=3)", ylim=ylim)
plot(ma(Nile, 7), main="Simple Moving Averages (k=7)", ylim=ylim)
plot(ma(Nile, 15), main="Simple Moving Averages (k=15)", ylim=ylim)
par(opar)
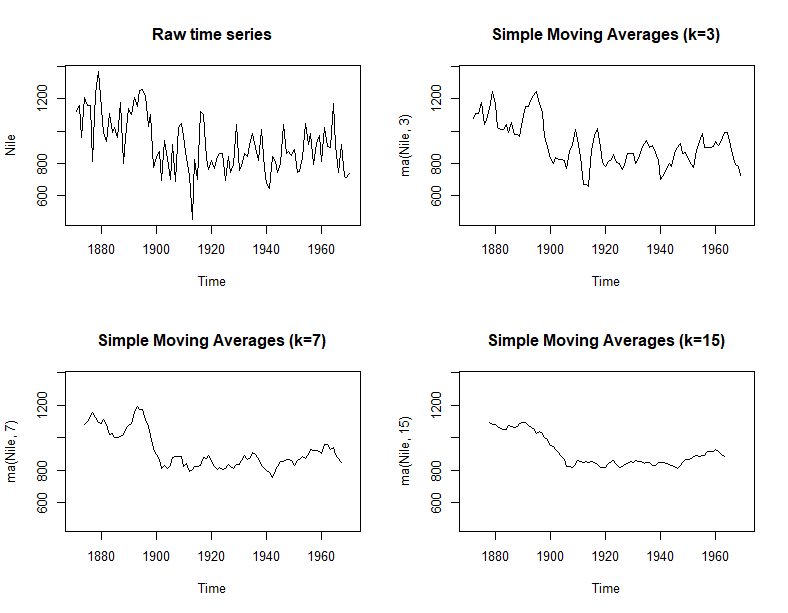
分解时序对象



- 实例
plot(AirPassengers)
可以看到趋势很明显,但是季节性波动越来越大,可能是个相乘性的模型

lAirPassengers <- log(AirPassengers)
plot(lAirPassengers, ylab="log(AirPassengers)")
可以看到做log转化后,方差稳定了,变成了趋势性季节性相加模型了

fit <- stl(lAirPassengers, s.window="period")
plot(fit)
log transform 的data
季节项随时间的变化
趋势项随时间的变化
随机误差项在时间点上的表现等

fit$time.series # log转化后的结果
exp(fit$time.series) # 原始尺度上的数值
季节项,趋势项,随机项的具体数值
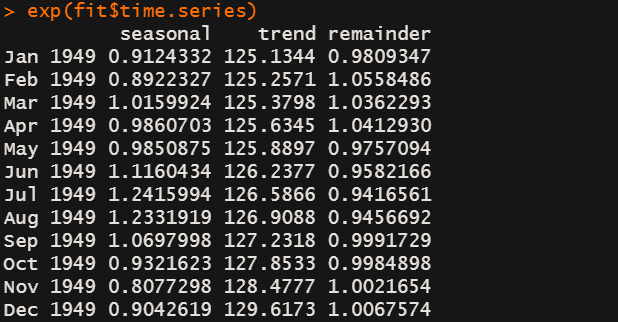
其他的季节性分解可视化函数:
par(mfrow=c(2,1))
library(forecast)
monthplot(AirPassengers, xlab="", ylab="")
seasonplot(AirPassengers, year.labels="TRUE", main="")

预测时间序列
指数预测模型


单指数预测模型





- 平均误差和平均百分比误差,误差值的和平均数,用处不大,正负误差会相互抵消
- RMSE:平均误差平方和的 平方根
- 平均绝对百分误差:误差在真实值中的占比,没有单位,可以用于比较不同模型的预测准确性
- 平均绝对标准化误差:也可以用来比较不同模型的预测准确性
holt指数预测测模型

library(forecast)
fit <- ets(log(AirPassengers), model="AAN")
fit # 返回 alpha beta 值
#评估模型
accuracy(fit)
# 进行预测
pred <- forecast(fit, 5)
pred
holt-winters指数预测模型

library(forecast)
fit <- ets(log(AirPassengers), model="AAA")
fit # 返回 alpha beta gamma值
#评估模型
accuracy(fit)
# 进行预测
pred <- forecast(fit, 5)
pred
ets()函数的其他能力


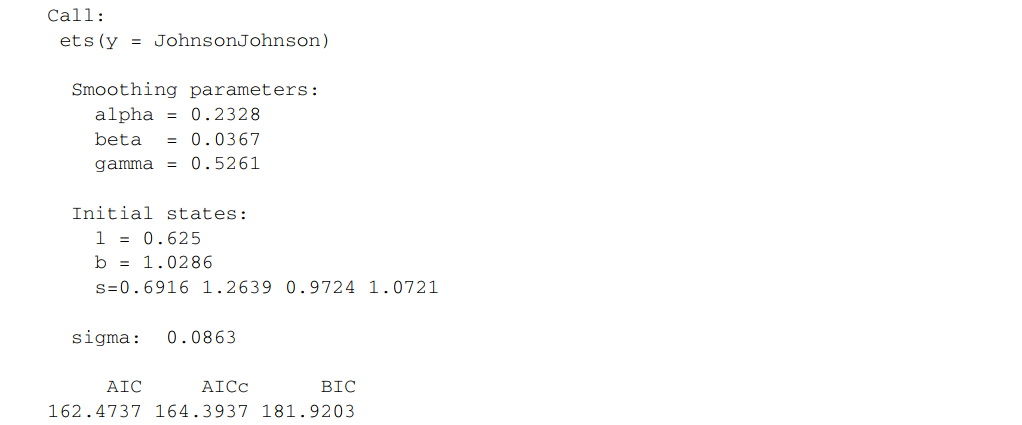
ARIMA预测模型
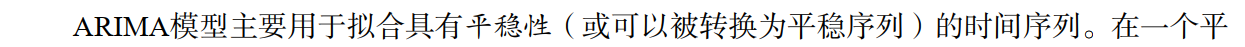



概念介绍部分
-
滞后阶数
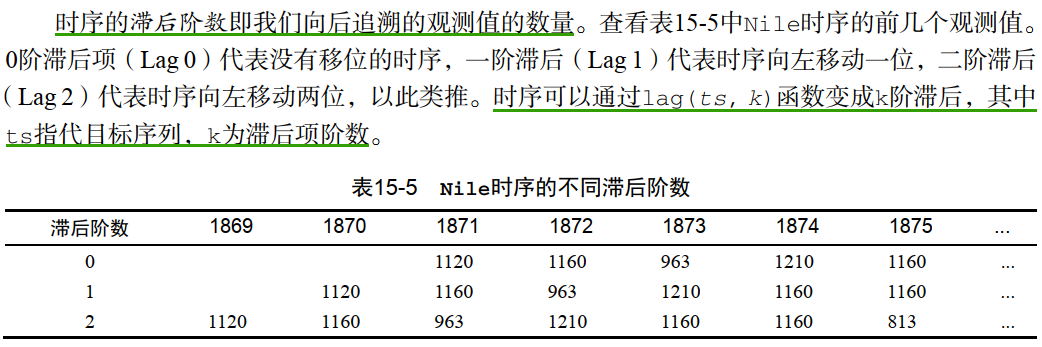
-
时序的自相关
ACk即一些列观察测值(Yt)和K时期之前的观测值(Yt-k)之间的相关性
比如,AC1就是1阶滞后序列与0阶滞后序列之间的相关性AC1,AC2,AC3…ACk构成的图即为自相关图(ACF图)
stats包中的acf()函数或者forecast包中的Acf()函数可以生成ACF图
-
时序的偏相关

-
差分
就是将序列中的观测值Yt 变为 Yt-1 - Yt


-
自回归项
AutoRegressive, AR项 -
移动平均项
Moving Averages, MA项
模型简介


- 验证序列的平稳性
可以先做差分图看看,在做ADF统计检验看看
library(forecast)
plot(Nile)
ndiffs(Nile) # 自动检测最佳的差分数d等于几
dNile <- diff(Nile)
plot(dNile)
貌似差分后数据在均值附近波动了

library(tseries)
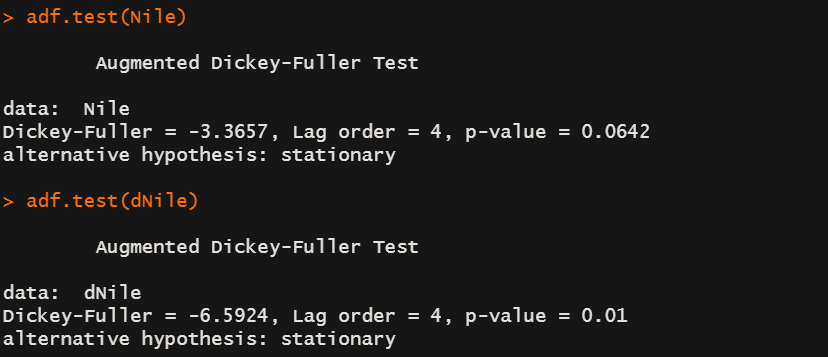
adf.test(Nile)
adf.test(dNile)
前面说过ADF检验P值显著性说明方差稳定
- 模型选择
可以根据ACF 和PACF图选择模型参数
# 针对的都是差分后的数据
Acf(dNile) # 自相关
Pacf(dNile) #偏自相关


- 拟合模型
library(forecast)
fit <- arima(Nile, order=c(0,1,1)) #ts=时序,order=c(p,d,q)
fit

- 模型评价

qqnorm(fit$residuals)
qqline(fit$residuals)
残差项或者说误差项满足正态性则会分布在直线上

检验残差值的相关性系数是否显著不为0

- 预测
用forecast进行预测,forecast(model,k)
forecast(fit, 3)
自动预测
library(forecast)
fit <- auto.arima(sunspots)
fit #返回比较合适的模型参数