自适应遗传算法求解TSP问题（Java）

news2024/9/28 5:30:49

1 引言

普通遗传算法（Sample Genetic Algorithm, SGA）存在着严重的缺点，它的Pc和Pm的值是固定的，本文采用自适应遗传算法进行求解TSP问题。不管是优良个体还是劣质个体都经过了相同概率的交叉和变异操作。这会引起两个很严重的问题：

  1. 相同的概率，这可以说是不公平，因为对于优良个体，我们应该减小交叉变异概率，使之能够尽量保存 ； 而对于劣质个体，我们应该增大交叉变异概率，使之能够尽可能的改变劣质的状况 。所以，一成不变的交叉变异概率影响了算法的效率。
  2. 相同的概率总不能很好的满足种群进化过程中的需要，比如在迭代初期，种群需要较高的交叉和变异概率，已达到快速寻找最优解的目的，而在收敛后期，种群需要较小的交叉和变异概率，以帮助种群在寻找完最优解后快速收敛。所以，一成不变的交叉变异概率影响了算法的效率。

2 问题描述

TSP问题共有3种数学模型，如下。另有https://blog.csdn.net/Zhang_0702_China/article/details/106983492给出了TSP几种建模方式详细介绍。

  1. 消除子回路约束模型（本文采用，下图）
  2. MTZ约束消除子回路模型，Miller-Tucker-Zemlin formulation
  3. 1-tree模型
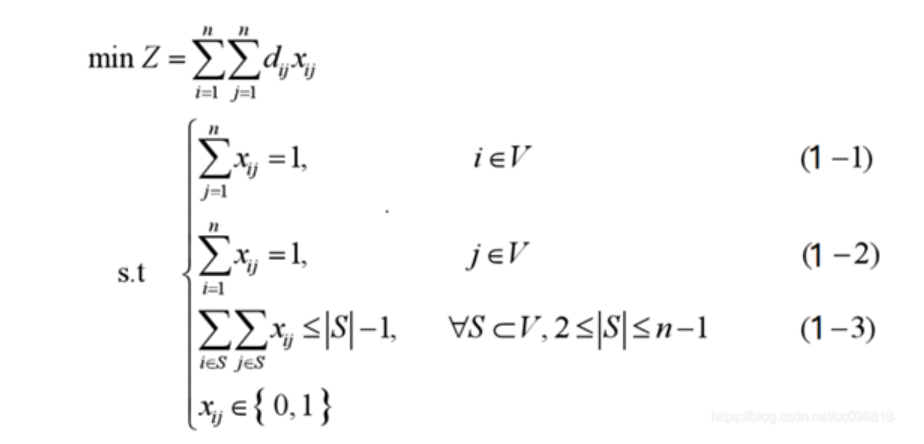
    在这里插入图片描述

3 遗传算法

3.1初始种群生成

种群规模设置为100，随机城市顺序，采用自然数编码方式构造染色体，用0-19表示20个城市，染色体的编码如图所示，每条染色体表示城市访问顺序。如下图表示为：该旅行商从城市2出发，走到城市8，最后回到城市2。在这里插入图片描述
3.2适应度计算
适应度函数是非负的，任何情况下总希望越大越好。TSP问题的目标函数是总距离越小越好，所以设计适应度函数为 f i t n e s s = 1 z fitness=\frac{1}{z} fitness=z1​

3.3 选择操作（精英策略+轮盘赌策略）
精英策略：即选择父代中适应度最大的个体遗传到子代。
轮盘赌选择：计算产生新个体的适应值，根据适应值大小分配个体的概率，根据概率方式选择个体作为下一代种群的父代。基本思想：各个个体被选中的概率与其适应度大小成正比,适应度值越好的个体，被选择的概率就越大。轮盘赌选择步骤如下：

  1. 计算适应度：适应度为该条染色体（一条可行路径）的总距离的倒数
  2. 计算每个个体的选择概率：选择概率是个体被遗传到下一代的概率，显然适应度愈大，该个体愈能适应环境，遗传到下一代的概率更高。染色体 i i i的选择概率计算公式为 p i ( s e l e c t ) = f i t n e s s i ∑ i = 1 N f i t n e s s i p_i(select)=\frac{fitness_i}{\sum_{i=1}^N{fitness_i}} pi​(select)=∑i=1N​fitnessi​fitnessi​​ ，其中 i i i代表个体， N N N代表种群规模。
  3. 计算每个个体的累积概率： p i ( c u l ) = ∑ j = 1 i p j ( s e l e c t ) p_i(cul)=\sum_{j=1}^i{p_j(select)} pi​(cul)=∑j=1i​pj​(select)
  4. 执行精英策略：在当代种群population中把选择概率最大的个体，直接复制到子代种群offspring，即offspring[1] = population[argmax(p_select)]，其中p_select= { p i ( s e l e c t ) } i = 1 N \{p_i(select)\}_{i=1}^N {pi​(select)}i=1N​
  5. 执行轮盘赌选择：对每个个体 i i i，在[0, 1]区间生成一个随机数 r i r_i ri​，若 p i − 1 ( c u l ) ≤ r i ≤ p i ( c u l ) p_{i-1}(cul) \leq r_i \leq p_i(cul) pi−1​(cul)≤ri​≤pi​(cul)，则个体i被选择至下一代。
  6. 重复步骤5，N-1次。

3.4 交叉算法

随机选择两条染色体 chrom1和chrom2，确定两个切点cut1和cut2，如cut1=2，cut2=4，则交换chrom1和chrom2的黄色部分。

在这里插入图片描述

交换完成后如下图：
在这里插入图片描述

此时，chrom1和chrom2都含有重复的基因，chrom1的基因0（城市1）重复，chrom2的基因1（城市3）重复（即绿色部分）
在这里插入图片描述

将绿色部分调整，一个思路是采用映射表。调整过程如下：
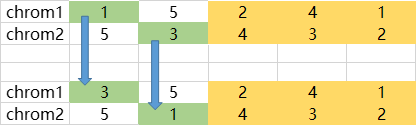
在这里插入图片描述

黄色部分（交叉片段）即为映射表（如下），即检查为参与交叉的基因，若该基因在映射表中，则按映射表进行互换。如上如chrom1中，城市1和城市5为非交叉基因，城市1在映射表中需替换为城市2，又城市2需替换为城市4，又城市4需替换为城市3。最终城市1替换为城市3。
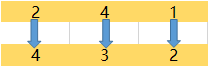
在这里插入图片描述

3.5 变异算法

采用2-opt方法，即选择染色体，随机选择2个位置，将这两个位置的基因交换，如下图。
在这里插入图片描述

3.6 停止准则

停止准则有3种，本文选择第三种。

  1. 当最优个体的适应度达到给定的阈值
  2. 最优个体的适应度和群体适应度不再上升
  3. 迭代次数达到预设的代数时，算法终止（本文采用）

4 运行结果

运行一把迭代10000次结果如下，800多就逼近最优解：

Iteration: 0 path: [11, 17, 4, 2, 15, 10, 14, 18, 7, 12, 19, 8, 9, 5, 3, 1, 6, 16, 13, 0] distance: 1729.0
Iteration: 200 path: [15, 18, 17, 14, 11, 8, 4, 2, 9, 12, 13, 10, 7, 5, 3, 1, 6, 16, 19, 0] distance: 1122.0
Iteration: 400 path: [15, 18, 17, 14, 11, 8, 4, 2, 9, 12, 19, 16, 13, 10, 6, 1, 3, 7, 5, 0] distance: 893.0
Iteration: 600 path: [15, 18, 17, 14, 11, 8, 4, 5, 9, 12, 19, 16, 13, 10, 6, 1, 3, 7, 2, 0] distance: 887.0
Iteration: 800 path: [15, 18, 17, 14, 11, 8, 4, 5, 9, 12, 19, 16, 13, 10, 6, 1, 3, 7, 2, 0] distance: 887.0
Iteration: 1000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 10000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
time used: 1s

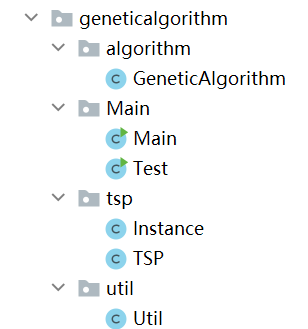
程序

  1. GeneticAlgorithm遗传算法
  2. Main运行
  3. Instance读取文件（20个城市的坐标，）
  4. Util类：一些工具方法
    在这里插入图片描述
package geneticalgorithm.algorithm;

import geneticalgorithm.util.Util;
import geneticalgorithm.tsp.TSP;

import java.util.*;

public class GeneticAlgorithm {
    TSP tsp;
    //距离矩阵
    double[][] distance;
    //种群规模
    int size;
    //基因数量
    int gene;
    //父代种群
    int[][] parent;
    //适应度
    double[] fitness;
    //子代种群
    int[][] child;

    //最大迭代次数
    private final int GEN;
    //交叉概率
    private double pcrossover;
    //变异概率
    private double pmutation;

    public GeneticAlgorithm(String fileName, int GEN) {
        tsp = new TSP(fileName);
        distance = tsp.distance;
        pcrossover = 0.;
        pmutation = 0.;
        this.GEN = GEN;
    }

    public void initialize(int size) {
        this.size = size;
        gene = distance.length;
        parent = new int[size][gene];
        fitness = new double[size];
        child = new int[size][gene];
    }

    private void initializePopulation() {
        int size = parent.length;
        for (int i = 0; i < size; i++) {
            parent[i] = Util.randArr(gene);
        }
    }

    //适应度函数
    private void fitness() {
        for (int i = 0; i < parent.length; i++)
            fitness[i] = 1000000.0 / getLen(parent[i]);
        updateProbality();
    }

    //更新交叉概率、变异概率
    private void updateProbality() {
        //最大适应度
        double fmax = Util.max(fitness);
        //平均适应度
        double favg = Util.sum(fitness) / size;
        pcrossover = 100 / (fmax - favg);
        pmutation = 100 / (fmax - favg);
    }

    /**
     * @param chrom 染色体
     * @return 一条染色体的总距离
     */
    private double getLen(int[] chrom) {
        double len = 0;
        for (int k = 0; k < chrom.length - 1; k++) {
            int i = chrom[k];
            int j = chrom[k + 1];
            len += distance[i][j];
        }
        len = len + distance[chrom[chrom.length - 1]][0];
        return len;
    }

    //选择操作
    private void select() {
        eliteSelect();
        routtleSelect();
    }

    //精英选择1条染色体
    private void eliteSelect() {
        int elite = Util.getMaxIndex(fitness);
        updatePopulation(parent, child, elite, 0);
    }

    //轮盘赌选择99条染色体
    private void routtleSelect() {
        double[] cumul = cumulativep();
//        System.out.println(Arrays.toString(cumulativep()));
        for (int i = 1; i < parent.length; i++) {
            double randDouble = Math.random();
            int selected = 0;
            for (int j = 0; j < cumul.length; j++) {
                if (randDouble < cumul[j]) {
                    selected = j;//选择第j条染色体
                    break;
                }
            }
            updatePopulation(parent, child, selected, i);
        }
    }

    //更新种群
    private void updatePopulation(int[][] parent, int[][] child, int selected, int i) {
        System.arraycopy(parent[selected], 0, child[i], 0, gene);
    }

    //累积概率
    private double[] cumulativep() {
        double[] cumulativep = new double[size];
        double[] slectionp = slectionp();
        for (int i = 0; i < size; i++) {
            double res = 0.;
            for (int j = 0; j <= i; j++) {
                res += slectionp[j];
            }
            cumulativep[i] = res;
        }
        return cumulativep;
    }

    //选择概率
    private double[] slectionp() {
        double[] selectionp = new double[size];
        for (int i = 0; i < size; i++)
            selectionp[i] = fitness[i] / Util.sum(fitness);
        return selectionp;
    }

    public void cross() {
        int ch1 = Util.randInt(size - 1) + 1;
        int ch2 = Util.randInt(size - 1) + 1;//不选择精英个体
        int[] chrom1 = child[ch1];
        int[] chrom2 = child[ch2];
        cross(chrom1, chrom2);
    }

    private void cross(int[] chrom1, int[] chrom2) {
        int cut1 = Util.randInt(gene);
        int cut2 = Util.randInt(cut1, gene - 1);
        int[][] map = new int[cut2 - cut1 + 1][2];
        swap(chrom1, chrom2, map, cut1, cut2);
        adjust(chrom1, chrom2, map, cut1, cut2);
    }

    private void swap(int[] chrom1, int[] chrom2, int[][] map, int cut1, int cut2) {
        for (int i = cut1; i <= cut2; i++) {
            map[i - cut1][0] = chrom1[i];
            map[i - cut1][1] = chrom2[i];
            chrom1[i] = map[i - cut1][1];
            chrom2[i] = map[i - cut1][0];
        }
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map.length; j++) {
                if (map[i][0] == map[j][1]) {
                    map[i][0] = map[j][0];
                    map[j][1] = map[i][1];
                    map[i][0] = map[i][1] = -1;
                }
            }
        }
    }

    private static void adjust(int[] chrom1, int[] chrom2, int[][] map, int cut1, int cut2) {
        for (int i = 0; i < chrom1.length; i++) {
            if (i < cut1 || i > cut2)
                for (int[] ints : map) {
                    if (chrom1[i] == ints[1]) chrom1[i] = ints[0];
                    if (chrom2[i] == ints[0]) chrom2[i] = ints[1];
                }
        }

    }

    public void mutate() {
        //i从1开始 保留精英
        for (int i = 1; i < child.length; i++) {
            int r1 = Util.randInt(20);//产生[0,20)的随机整数
            int r2 = Util.randInt(20);
            int gene1 = child[i][r1];
            int gene2 = child[i][r2];
            child[i][r1] = gene2;
            child[i][r2] = gene1;

        }
    }


    public void runGeneticAlgorithm() {
        initializePopulation();
        fitness();
        long start = System.currentTimeMillis();
        for (int gen = 0; gen <= GEN; gen++) {
            select();
            if (Math.random() < pcrossover) cross();
            if (Math.random() < pmutation) mutate();
            for (int i = 0; i < child.length; i++) parent[i] = child[i].clone();
            for (int i = 0; i < child.length; i++) {
                if (Util.isRepetition(child[i])) {
                    System.out.println(Arrays.toString(child[i]));
                    throw new IllegalArgumentException("repetition!");
                }

            }

            fitness();
            displayInfo(gen);
        }
        long end = System.currentTimeMillis();
        System.out.printf("time used: %ss", (end - start) / 1000);
    }

    private void displayInfo(int counter) {
        if (counter % 200 == 0) {
            int ch = Util.getMaxIndex(fitness);
            System.out.println();
            System.out.printf("Iteration: %s\t", counter);
            System.out.printf("     path: %s\t", Arrays.toString(child[ch]));
            System.out.printf(" distance: %s", getLen(child[ch]));

            System.out.println();
        }
    }

}

package geneticalgorithm.tsp;

import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;

public class Instance {

    public double[][] readFile(String filename) {
        double[] x = new double[20];
        double[] y = new double[20];
        double[][] distance = new double[x.length][y.length];
        try (BufferedReader bf = new BufferedReader(new FileReader(filename))) {
            int counter = 0;
            String line;
            while ((line = bf.readLine()) != null) {
                String[] coordinate = line.split(",");
                x[counter] = Double.parseDouble(coordinate[0]);
                y[counter] = Double.parseDouble(coordinate[1]);
                counter += 1;
            }
        } catch (IOException e) {
            System.out.println("File not found!");
            System.exit(-1);
        }

        for (int i = 0; i < x.length; i++) {
            distance[i][i] = 0;
            for (int j = 0; j < y.length; j++) {
                double e1 = Math.abs((x[i] - x[j]));
                double e2 = Math.abs((y[i] - y[j]));
                distance[i][j] = distance[j][i] = (int) Math.sqrt(e1 * e1 + e2 * e2);
            }
        }
        return distance;
    }

}

package geneticalgorithm.tsp;

import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;

public class Instance {

    public double[][] readFile(String filename) {
        double[] x = new double[20];
        double[] y = new double[20];
        double[][] distance = new double[x.length][y.length];
        try (BufferedReader bf = new BufferedReader(new FileReader(filename))) {
            int counter = 0;
            String line;
            while ((line = bf.readLine()) != null) {
                String[] coordinate = line.split(",");
                x[counter] = Double.parseDouble(coordinate[0]);
                y[counter] = Double.parseDouble(coordinate[1]);
                counter += 1;
            }
        } catch (IOException e) {
            System.out.println("File not found!");
            System.exit(-1);
        }

        for (int i = 0; i < x.length; i++) {
            distance[i][i] = 0;
            for (int j = 0; j < y.length; j++) {
                double e1 = Math.abs((x[i] - x[j]));
                double e2 = Math.abs((y[i] - y[j]));
                distance[i][j] = distance[j][i] = (int) Math.sqrt(e1 * e1 + e2 * e2);
            }
        }
        return distance;
    }

}

package geneticalgorithm.Main;

import geneticalgorithm.algorithm.GeneticAlgorithm;

public class Main {
    public static void main(String[] args) {
        String fileName = "D:\\Users\\36297\\JavaWorkspace\\algori\\src\\tsp\\geneticalgori\\data.txt";
        GeneticAlgorithm ga = new GeneticAlgorithm(fileName,10000);
        ga.initialize(500);
            ga.runGeneticAlgorithm();
    }
}

package geneticalgorithm.util;

import java.util.Arrays;
import java.util.HashSet;
import java.util.Random;
import java.util.Set;
import java.util.concurrent.ThreadLocalRandom;

public class Util {
    /**
     * @param n [0-n]长度
     * @return [0-n]范围不重复的随机数组
     */
    public static int[] randArr(int n) {
        return ThreadLocalRandom.current().ints(0, n).distinct().limit(n).toArray();
    }

    /**
     * @param array 一维数组
     * @return maximum element of an integer array
     */
    public static int max(int[] array) {
        return Arrays.stream(array).max().getAsInt();
    }

    /**
     * @param array integer array
     * @return index of the max
     */
    public static int getMaxIndex(int[] array) {
        double max = max(array);
        for (int i = 0; i < array.length; i++)
            if (max == array[i]) return i;
        return -1;
    }

    /**
     * @param array 一维数组
     * @return maximum element of an double array
     */
    public static double max(double[] array) {
        return Arrays.stream(array).max().getAsDouble();
    }

    /**
     * @param array double array
     * @return index of the max
     */
    public static int getMaxIndex(double[] array) {
        double max = max(array);
        for (int i = 0; i < array.length; i++)
            if (max == array[i]) return i;
        return -1;
    }

    /**
     * @param array double array
     * @return 数组求和
     */
    public static double sum(double[] array) {
        return Arrays.stream(array).sum();
    }

    /**
     * @param index [0,index)
     * @return 返回[0, index)的一个随机整数
     */
    public static int randInt(int index) {
        return new Random().nextInt(index);
    }

    /**
     * @param min [min,max)
     * @param max [min,max)
     * @return [min, max)间的一个随机数
     */
    public static int randInt(int min, int max) {
        return (int) (Math.random() * (max + 1 - min) + min);
    }

    public static boolean isRepetition(int[] args) {
        Set<Object> set = new HashSet<>();
        for (int arg : args) set.add(arg);
        return set.size() != args.length;
    }
}

数据 城市坐标

60,200
180,200
80,180
140,180
20,160
100,160
200,160
140,140
40,120
100,120
180,100
60,80
120,80
180,60
20,40
100,40
200,40
20,20
60,20
160,20

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/429964.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux驱动开发——高级I/O操作（二）

Linux驱动开发——高级I/O操作（二）

目录 proc文件操作 非阻塞型I/O 阻塞型I/O proc文件操作 proc 文件系统是一种伪文件系统&#xff0c;这种文件系统不存在于磁盘上&#xff0c;只存在于内存中只有内核运行时才会动态生成里面的内容。这个文件系统通常挂载在/proc 目录下&#xff0c;是核开发者向用户导出信息…
阅读更多...
公司招人，面试了50+的候选人，技术实在是太烂了····

公司招人，面试了50+的候选人，技术实在是太烂了····

前两个月&#xff0c;公司测试岗位面了 50候选人&#xff0c;面试下来发现几类过不了的情况&#xff0c;分享大家防止踩坑&#xff1a; 技术倒是掌握得挺多&#xff0c;但只是皮毛&#xff0c;基础知识却是一塌糊涂。工作多年&#xff0c;从未学习过工作之外的技术栈&#xff…
阅读更多...
ERTEC200P-2 PROFINET设备完全开发手册(7-1）

ERTEC200P-2 PROFINET设备完全开发手册(7-1）

7. 配置模块及自定义模块 7.1.1 PN设备的基本模型 初次接触PN的开发者&#xff0c;最容易出现的错误就是设备的实际配置与TIA的组态不一致。为了开发的过程更加顺利&#xff0c;非常有必要掌握PN设备的基础模型。PN设备的基本模型如下图描述&#xff1a; PN设备的基本构成是插…
阅读更多...
No.039＜软考＞《（高项）备考大全》【第23章】综合测试管理

No.039＜软考＞《（高项）备考大全》【第23章】综合测试管理

【第23章】综合测试管理1 章节相关1.1 考试相关1.2 案例相关2 测试监控3 测试风险管理4 测试人员绩效考核4.1 测试分类测试类型分类执行方式分类开发阶段分类5 开发测试分类参考答案1 章节相关 1.1 考试相关 必考1分选择&#xff0c;案例概率低。 1.2 案例相关 2020年下半年…
阅读更多...
关于IOS系统时间格式显示NAN问题以及小程序项目运行报错app.json找不到

关于IOS系统时间格式显示NAN问题以及小程序项目运行报错app.json找不到

目录 问题一&#xff1a;关于IOS系统时间格式显示NAN 一、比较常见的情况&#xff0c;时间格式为"yyyy-MM-dd HH:mm:ss"格式在 iOS 会出现 NAN 二、关于时间临界值&#xff1a;对于00:00:00和24:00:00这两个时间临界值, ios会转成NAN 三、时间格式为2022/09&#…
阅读更多...
Java语法理论和面经杂疑篇《六.泛型(Generic)》

Java语法理论和面经杂疑篇《六.泛型(Generic)》

1. 泛型概述 1.2 泛型的引入 在Java中&#xff0c;我们在声明方法时&#xff0c;当在完成方法功能时如果有未知的数据需要参与&#xff0c;这些未知的数据需要在调用方法时才能确定&#xff0c;那么我们把这样的数据通过形参表示。在方法体中&#xff0c;用这个形参名来代表那…
阅读更多...
Medical X-rays Dataset汇总（长期更新）

Medical X-rays Dataset汇总（长期更新）

目录​​​​​​​ ChestX-ray8 ChestX-ray14 VinDr-CXR VinDr-PCXR ChestX-ray8 ChestX-ray8 is a medical imaging dataset which comprises 108,948 frontal-view X-ray images of 32,717 (collected from the year of 1992 to 2015) unique patients with the text-mi…
阅读更多...
Nginx(下载安装、常用命令、反向代理、负载均衡)

Nginx(下载安装、常用命令、反向代理、负载均衡)

官网&#xff1a;https://nginx.org/Nginx是一款轻量级的Web服务器/反向代理服务器及电子邮件&#xff08;IMAP/POP3&#xff09;代理服务器,其特点是占有内存少&#xff0c;并发能力强。下载和安装下载在Nginx的官网的下载页面中(http://nginx.org/en/download.html)&#xff…
阅读更多...
01、Cadence使用记录之新建工程与基础操作（原理图绘制：OrCAD Capture CIS）

01、Cadence使用记录之新建工程与基础操作（原理图绘制：OrCAD Capture CIS）

01、Cadence使用记录之新建工程与基础操作&#xff08;原理图绘制&#xff1a;OrCAD Capture CIS&#xff09; 硕士学电磁场去了&#xff0c;写点博客记录下学习过程。 参考的教程是B站的视频&#xff1a;allegro软件入门视频教程全集100讲 本科的时候就对Cadence有所耳闻&am…
阅读更多...
网络安全漏洞分析与漏洞复现

网络安全漏洞分析与漏洞复现

前言 4 月 6 日和 5 月 18 日&#xff0c;VMware 官方发布的两则安全公告中显示&#xff0c;关乎旗下产品的 CVE 漏洞多达 10 个&#xff0c;其中不乏有 CVSSv3 评分 9.8 的高危漏洞&#xff01;如此高频的出洞速率&#xff0c;吸引了笔者注意。笔者将对 CVE-2022-22954 VMwar…
阅读更多...
用CTGAN生成真实世界的表格数据

用CTGAN生成真实世界的表格数据

随着CLIP和稳定模型的快速发展&#xff0c;图像生成领域中GAN已经不常见了&#xff0c;但是在表格数据中GAN还是可以看到它的身影。 现实世界的复杂性与许多方面相关(例如&#xff0c;缺失数据、不平衡数据、噪声数据)&#xff0c;但最常见的一个问题是包含异构(或“混合”)数…
阅读更多...
软考电子商务设计师如何备考？

软考电子商务设计师如何备考？

关于软考电子商务设计师考什么?如何备考&#xff1f; 一、电子商务设计师概述&#xff1f; 电子商务设计师属于软考中级资格考试&#xff0c;软考是由国家人力资源和社会保障部&#xff08;原人事部&#xff09;、工业和信息化部&#xff08;原信息产业部&#xff09;领导的…
阅读更多...
使用Softing edgePlug软件扩展数控机床的连接性

使用Softing edgePlug软件扩展数控机床的连接性

那些使用SINUMERIK 840D控制器来运行数控机床的制造商正面临着一个挑战——从车间提取机床性能和过程数据来进行分析。这些数据对于优化流程至关重要&#xff0c;但它们却无法通过传统方式来被获取。对此&#xff0c;制造商的应对方法是通过自定义代码来实现数据访问&#xff0…
阅读更多...
Redis与MySQL的双写一致性问题

Redis与MySQL的双写一致性问题

Redis与MySQL的双写一致性问题更新缓存&#xff1f; 删除缓存&#xff1f;先更新缓存再更新数据库先更新数据库&#xff0c;再更新缓存先删除缓存再更新数据库先更新数据库&#xff0c;再删除缓存解决方案1. 重试2. 异步重试2.1 使用消息队列实现重试2.2 Binlog实现异步重试删除…
阅读更多...
10万字智慧政务大数据治理平台解决方案（word）

10万字智慧政务大数据治理平台解决方案（word）

本资料来源公开网络&#xff0c;仅供个人学习&#xff0c;请勿商用&#xff0c;如有侵权请联系删除。 1 项目整体建设规划方案 按照《省人民政府关于推进数字政府建设的指导意见》(鄂政发(2019) 4号&#xff09;的规则要求&#xff0c;结合XX市“互联网政府服务”建设现状&…
阅读更多...
【Android笔记93】Android小案例（三）之模仿小米商城（首页商品展示界面）

【Android笔记93】Android小案例（三）之模仿小米商城（首页商品展示界面）

这篇文章，主要介绍Android小案例（三）之模仿小米商城（首页商品展示界面）。 一、模仿小米商城（首页布局） 1.1、首页运行效果 这篇文章实现的首页布局界面如下所示： 1.2、实现思路 首页轮播图，这里采用一个Banner组件实现，不知道的可以看下我之前写的一篇文章【【And…
阅读更多...
DUET详解草稿

DUET详解草稿

详解VLN动机&#xff1a;流程拓扑图Text EncoderCoarse-scale Cross-modal EncoderNode embeddingGraph-aware cross-modal encodingGlobal action predictionFine-scale Cross-modal EncoderVisual EmbeddingFine-grained cross-modal reasoningLocal action prediction and o…
阅读更多...
heic格式怎么改成jpg？

heic格式怎么改成jpg？

你想知道heic格式怎么改成jpg吗&#xff1f;当我们面对heic格式图片时&#xff0c;很有可能就会遇到无法打开图片的情况。因为heic与JPG相比&#xff0c;heic格式占用空间更少&#xff0c;图像质量更无损。HEIC格式照片支持iOS11和macOS High Sierra(10.13)及更高版本。但是这种…
阅读更多...
【数据结构】链表 详解

【数据结构】链表 详解

我们不废话&#xff0c;直入正题。引入什么是链表&#xff1f;来看看百度怎么说&#xff1a;链表是一种物理存储单元上非连续、非顺序的存储结构&#xff0c;数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点&#xff08;链表中每一个元素称为结点&#…
阅读更多...
STM32+ESP8266点灯（STA 模式）点灯（2）

STM32+ESP8266点灯（STA 模式）点灯（2）

1、简介 STM32ESP8266点灯&#xff08;APSTA 模式&#xff09;点灯&#xff08;1&#xff09;一文已经通过串口助手实现与网络调试助手透传&#xff0c;本文通过STM32单片机替代网络调试助手&#xff0c;实现远程点灯。 2、单片机配置 2.1 cubemax配置 2.1.1 RCC配置 2.1.2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023