目录

函数的极限：

自变量趋向于有限值时函数的极限

左右极限

 需要分左右极限的三种问题：

 例题：

 极限性质：

函数的保号性：

函数的保号性：

例题：

 极限值与无穷小的关系

极限存在准则：

 无穷小量：

 无穷小的性质

 无穷大量：

无穷大量的比较

例题：

无穷大量的性质：

无穷大量与无界变量的关系

例题

无穷大量与无穷小量的关系

---

函数的极限：

 我们对定义进行解析：

 

 f(x)自变量趋向于无穷的极限存在的条件是函数趋向于负无穷和函数趋向于正无穷的极限值都存在并且相等。

 例如：

自变量趋向于有限值时函数的极限

 

 几何意义：

 注意：f(x)在x0处的极限值与这一点的函数值或者这一点是否有定义没有任何的关系，f(x)在x0处的极限值关注的是x0附近的变化趋势。

例如：

 

 所以上面的两种写法都是错误的，正确的写法需要保证三角或者方框在x=0附近的取心领域内不等于0.

左右极限

 

同样的，函数在某一点处的极限值为A的充要条件是左右极限值都存在并且都等于A。

 需要分左右极限的三种问题：

 

 我们分别对2和3举一个例子：

 例题：

 

 

 

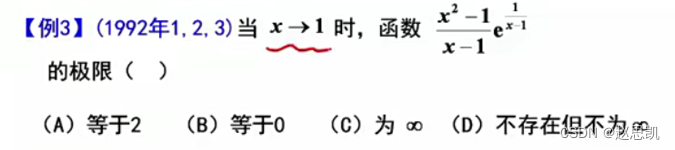
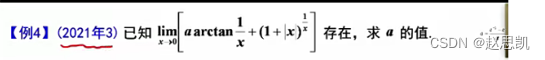
 极限性质：

 收敛数列必有界。

收敛表示有极限，假如极限值为A，则数列的后面的无限项全部趋近与A，所以这无限项被控制住了，因为有限项不需要控制，所以收敛数列必有界。

 对于函数来说，函数有极限的话，因为函数的前面和后面的项数都是无限的，所以我们只能保证函数在去心领域内部是有界的。

函数的保号性：

一句话来概述这个定义：当数列的极限值为A时，可以保证后面数列的无限项与极限值同号。

 这就叫做从极限值正负保数列的正负。

这里不能写等于,例如：

 如果数列后面无限项的值同号，则数列的极限值与无限项的值的符号相同。

函数的保号性：

 函数的保号性与数列的保号性的不同点是函数的保号性数列后的无限项与函数的去心领域的区别。

例题：

 

 极限值与无穷小的关系

 函数的极限值为A的充要条件是函数等于极限值加上无穷小值。

极限存在准则：

 

 一句话简述：在数列的无限项中，假如数列A始终大于等于数列B小于等于数列c。

而数列B和数列C在n趋向于无穷时的极限值都为a，那么夹在中间的数列A在n趋向于无穷时的极限值也为a。

 单调增的数列第一项就是下界，单调减的数列的第一项就是下界。

 例如：

 

 

 

 

 

 无穷小量：

 当函数的在x0处的极限值为0，就叫做f(x)为x趋向于x0时的无穷小量。

无穷小的阶数我们可以这样理解：高阶的无穷小比低阶的无穷小趋向于0的速度更快。

 

 无穷小的性质

 无限个无穷小的和是不是无穷小呢？

不是，我们举一个例子：

 我们再举一个例子：

无穷小乘以有界变量的结果为无穷小，所以结果为无穷小 对吗？

不对： 

 无穷大量：

无穷大量的比较

 对于函数来说，指数大于幂函数大于对数函数。

对于数列来说，n的n次方大于n的阶乘大于指数大于幂函数大于对数。

例题：

 指数大于迷惑函数大于对数，所以选择c

无穷大量的性质：

 有限个无穷大量的积仍为无穷大量。

无穷大量加上有界变量的结果仍未无穷大量。

无穷大量与无界变量的关系

 无穷大量是在后面的无限项|Xn|大于M

无界变量是只要有一项的结果使|Xn|大于M即可

所以无穷大量一定是无界变量，无界变量并不一定是无界变量。

例题

 

 

无穷大量与无穷小量的关系

 可以简单的理解为无穷大量与无穷小量互为倒数。